La proyección de homolosina de Goode (o proyección de homolosina de Goode interrumpida ) es una proyección de mapa compuesto pseudocilíndrica , de áreas iguales utilizada para los mapas del mundo . Normalmente se presenta con múltiples interrupciones. Su propiedad de área de igualdad lo hace útil para presentar la distribución espacial de los fenómenos.
La proyección fue desarrollada en 1923 por John Paul Goode para proporcionar una alternativa a la proyección de Mercator para retratar relaciones globales de área. Goode ofreció variaciones del esquema de interrupción para enfatizar las masas terrestres del mundo y los océanos del mundo. Algunas variantes incluyen extensiones que repiten regiones en dos lóbulos diferentes del mapa interrumpido para mostrar Groenlandia o Rusia oriental sin divisiones. El homolosine evolucionó a partir de los experimentos de Goode's de 1916 para interrumpir la proyección de Mollweide . [1]
Debido a que Mollweide a veces se denomina "proyección homolográfica", Goode fusionó los dos nombres "homolográfico" y "sinusoidal" para crear el nombre "homolosine". [2] Común en la década de 1960, la proyección homolosina de Goode a menudo se denomina "mapa de piel de naranja" debido a su parecido con la cáscara aplanada de una naranja pelada a mano. En su forma más común, el mapa interrumpe el Atlántico Norte, el Atlántico Sur, el Pacífico Sur, el Océano Índico y todo el meridiano este / oeste del mapa.
Hasta las latitudes 40 ° 44′11.8 "N / S, el mapa se proyecta de acuerdo con la transformación de la proyección sinusoidal . Las latitudes más altas son las secciones superiores de una proyección de Mollweide , injertadas en la sección media sinusoidal donde coincide la escala de las dos proyecciones. Este injerto da como resultado una torcedura en los meridianos a lo largo del paralelo del injerto. La propiedad del área de igualdad de la proyección se deduce del hecho de que sus proyecciones de origen son, a su vez, ambas áreas de igual área.
La proyección GS50 proporciona una proyección conforme solo para mapas de los 50 Estados Unidos. La escala varía menos del 2% en toda el área cubierta. La distorsión es muy baja también. No es una proyección estándar en el sentido de que utiliza polinomios complejos (del décimo orden) en lugar de una formulación trigonométrica, aunque se desarrolló a partir de una proyección estereográfica oblicua .
La proyección Guyou hemisferio-in-a-cuadrado es un conformal proyección del mapa para el hemisferio. Es un aspecto oblicuo de la proyección quincuncial de Peirce .
Historia [ editar ]
La proyección fue desarrollada por Émile Guyou de Francia en 1887. [1]
Descripción formal [ editar ]
La proyección se puede calcular como un aspecto oblicuo de la proyección quincuncial de Peirce girando el eje 45 grados. También se puede calcular girando las coordenadas −45 grados antes de calcular la proyección estereográfica; esta proyección se vuelve a asignar a un cuadrado cuyas coordenadas se giran 45 grados. [2]
La proyección es conforme a las cuatro esquinas de cada cuadrado del hemisferio. Al igual que otras proyecciones poligonales conformes, Guyou es un mapeo de Schwarz-Christoffel .
Propiedades [ editar ]
- Cada hemisferio se representa como un cuadrado, la esfera como un rectángulo de relación de aspecto 2: 1.
- La parte donde la exageración de la escala equivale a duplicar la del centro de cada cuadrado es solo el 9% del área de la esfera, contra el 13% para el Mercator y el 50% para el estereográfico [3]
- La curvatura de las líneas que representan grandes círculos es, en todos los casos, muy leve, sobre la mayor parte de su longitud. [3]
- Es conforme en todas partes, excepto en las esquinas del cuadrado que corresponde a cada hemisferio, donde dos meridianos cambian de dirección abruptamente dos veces cada uno; El ecuador está representado por una línea horizontal.
- Puede ser teselado en todas las direcciones.
Proyecciones relacionadas [ editar ]
- La proyección del hemisferio en cuadrado de Adams y la proyección quincuncial de Peirce son aspectos diferentes de la misma cartografía subyacente de Schwarz-Christoffel. Tales mapeos son transformaciones de media proyección estereográfica .
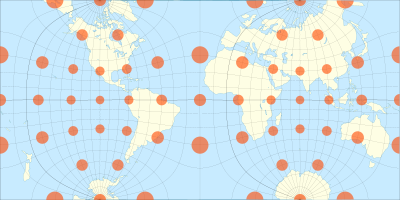
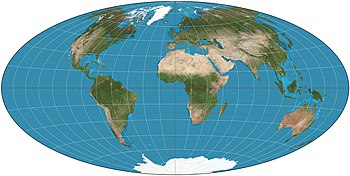
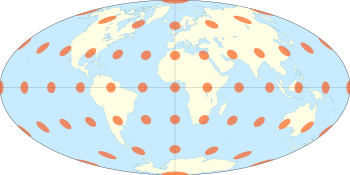
La proyección de Hammer es una proyección de mapa de áreas iguales descrita por Ernst Hammeren 1892. Usando la misma forma externa elíptica 2: 1 que la proyección de Mollweide , Hammer pretende reducir la distorsión en las regiones de los meridianos externos, donde es extrema en el Mollweide.
Desarrollo [ editar ]
Directamente inspirado por la proyección de Aitoff , Hammer sugirió el uso de la forma ecuatorial de la proyección de igual área acimutal de Lambert enlugar del uso de Aitoff de la proyección equidistante azimutal de Aitoff :
donde laea x y laea y son las componentes x y y de la proyección ecuatorial de igual área de Lambert de Lambert. Escrito explícitamente:
Lo inverso se calcula con la variable intermedia.
La longitud y las latitudes se pueden calcular por
Visualmente, las proyecciones de Aitoff y Hammer son muy similares. El Martillo ha visto un mayor uso debido a su propiedad de área de igualdad. La proyección de Mollweide es otra proyección de área similar de aspecto similar, aunque con paralelos rectos de latitud, a diferencia de los paralelos curvos del Martillo.
Briesemeister [ editar ]
William A. Briesemeister presentó una variante del Martillo en 1953. En esta versión, el meridiano central se establece en 10 ° E, el sistema de coordenadas se gira para que los 45 ° N sean paralelos al centro, y el mapa resultante se aplasta horizontalmente y se extienden recíprocamente verticalmente para lograr una relación de aspecto de 7: 4 en lugar del 2: 1 del martillo. El propósito es presentar las masas terrestres de manera más central y con menor distorsión. [3]
Nórdico [ editar ]
Antes de proyectar a Hammer, John Bartholomew rotó el sistema de coordenadas para llevar los 45 ° norte en paralelo al centro, dejando el primer meridiano como el meridiano central. Llamó a esta variante la proyección "nórdica".









No hay comentarios:
Publicar un comentario