Radian
Entender Radian Medida [ editar ]
Muchas unidades de medida provienen de raíces aparentemente arbitrarias y arcaicas. Algunos incluso cambiar con el tiempo. El metro, por ejemplo estaba destinado originalmente para ser basada en la circunferencia de la tierra y ahora tiene una definición científica increíblemente complicado! Normalmente utilizamos grados para medir ángulos. ¿Qué es exactamente un grado? Un grado es 1/360 º de una rotación completa alrededor de un círculo. Radianes son unidades alternativas utilizadas para medir ángulos en trigonometría. Así como suena, un radián se basa en el radio de un círculo. Un radián es el ángulo creado por la flexión de la longitud del radio alrededor del arco de un círculo. Debido a que un radián se basa en una parte real del círculo en lugar de una división arbitraria, es una unidad mucho más natural de la medida del ángulo para las matemáticas de nivel superior y será especialmente útil cuando se mueve a estudiar cálculo.
¿Qué pasaría si tuviéramos que girar todo el camino alrededor del círculo? Continuando añadir longitudes de radio, nos encontramos con que se necesita un poco más de 6 de ellos para completar la rotación.
Pero la longitud de arco de una rotación completa es realmente la circunferencia! La circunferencia es igual a los tiempos 2π la longitud del radio. 2π es de aproximadamente 6,28, por lo que la circunferencia es un poco más de 6 longitudes de radio. O, en términos de medida en radianes, una rotación completa (360 grados) es 2π radianes.
Con esto como punto de partida, podemos encontrar la medida en radianes de otros ángulos fácilmente. Por lo tanto, la mitad de una rotación, o 180 grados, debe ser radianes π, y 90 grados debe ser uno-media pi. Complete el siguiente cuadro:
| Ángulo en grados | Ángulo en radianes |
|---|---|
| 90 |  |
| 45 | |
| 30 | |
| 60 | |
| 75 |
Debido a que 45 es la mitad de 90, la mitad de la mitad π es un cuarto π. 30 es una tercera parte de un ángulo recto, de modo multiplicador da:
y porque 60 es dos veces tan grande como 30:
Aquí está la tabla completa:
| Ángulo en grados | Ángulo en radianes |
|---|---|
| 90 |  |
| 45 |  |
| 30 |  |
| 60 |  |
| 75 |  |
El último valor se encuentra sumando las medidas en radianes de 30 y 45:
Hay una fórmula para ayudar a convertir entre radianes y grados que es posible que ya han descubierto y discutiremos en breve, sin embargo, la mayoría de los ángulos que va a utilizar habitualmente se puede encontrar fácilmente de los valores de esta tabla, por lo que el aprendizaje basado en la circunferencia debería ayudar a aumentar su nivel de comodidad con radianes en gran medida. Por ejemplo, la mayoría de los estudiantes les resulta fácil de recordar 30 y 60. 30 es π más de 6 y 60 es π más de 3. Si conoces a estos ángulos, se puede encontrar cualquiera de los ángulos especiales que tienen ángulos de referencia de 30 y 60, ya que serán todos tienen los mismos denominadores. Lo mismo es cierto de múltiplos de pi más de 4 (45 grados) y más de 2 pi (90 grados).
"Cuenta" ing en radianes [ editar ]
¿Te acuerdas de cuando era niño viendo el conde en Sesame Street? Él sería contar objetos como manzanas, "una manzana, dos manzanas, tres manzanas ..." y luego se ríen diabólicamente como el relámpago y el trueno estallaron a su alrededor. Bueno, para ser exitoso con radianes, es necesario aprender a contar de nuevo usando radianes en lugar de manzanas. Vamos a empezar a contar los ángulos rectos, que son realmente  radianes.
radianes.
 radianes.
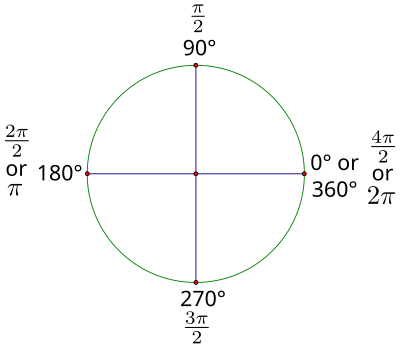
radianes.- " uno π más de 2, dos más de 2 π (en realidad sólo π), tres π más de 2, cuatro π más de 2 (que en realidad es 2π) "
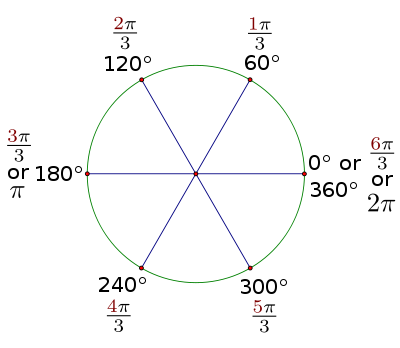
| Figura 2.1 : rotaciones de 90 grados expresados en radianes. |
Usted acaba cubierto todos los ángulos que son múltiplos de 90 grados en una rotación.
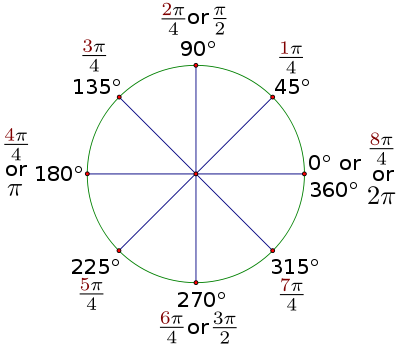
Aquí está el dibujo para ángulos de 45 grados:
| Figura 2.2 : rotaciones de 45 grados. |
Tenga en cuenta que los ángulos adicionales en el dibujo todos tienen ángulos de referencia de 45 grados y sus medidas radianes son todos múltiplos de  . Completa las siguientes medidas en radianes contando en múltiplos de
. Completa las siguientes medidas en radianes contando en múltiplos de  y
y  :
:
 . Completa las siguientes medidas en radianes contando en múltiplos de
. Completa las siguientes medidas en radianes contando en múltiplos de  y
y  :
:
|
|
| Figura 2.5 : 60 grados ángulo de referencia radianes través de una rotación. |
| Figura 2.6 : 30 grados ángulo de referencia radianes través de una rotación. |
Observe que todos los ángulos con ángulos de referencia de 60 grados son múltiplos de  , y todos los que tienen ángulos de referencia de 30 grados son múltiplos de
, y todos los que tienen ángulos de referencia de 30 grados son múltiplos de  Si usted puede aprender a contar en estos términos, en lugar de tener que constantemente convertir de nuevo a grados, le ayudará a tener trato eficaz con la mayoría de las medidas en radianes que encontrará.
Si usted puede aprender a contar en estos términos, en lugar de tener que constantemente convertir de nuevo a grados, le ayudará a tener trato eficaz con la mayoría de las medidas en radianes que encontrará.
 , y todos los que tienen ángulos de referencia de 30 grados son múltiplos de
, y todos los que tienen ángulos de referencia de 30 grados son múltiplos de  Si usted puede aprender a contar en estos términos, en lugar de tener que constantemente convertir de nuevo a grados, le ayudará a tener trato eficaz con la mayoría de las medidas en radianes que encontrará.
Si usted puede aprender a contar en estos términos, en lugar de tener que constantemente convertir de nuevo a grados, le ayudará a tener trato eficaz con la mayoría de las medidas en radianes que encontrará.
Para otros ejemplos hay una fórmula. Recuerda que:
Si divides ambos lados de esta igualdad por 180 que va a descubrir la fórmula para la conversión fácil:
así
Si tenemos una medida en grados y deseamos convertirlo a radianes, entonces la manipulación de la ecuación anterior da:
Ejemplo 1
Convertir
 a medida en grados. a medida en grados.
Solución :
Bueno, si has seguido la última sección, se debe reconocer que este ángulo es un múltiplo de
 (o 60 grados), por lo que hay 11 persona (o 60 grados), por lo que hay 11 persona  's en este ángulo: 's en este ángulo:  · 11 = 60 · 11 = 660 °. · 11 = 60 · 11 = 660 °.
Esto es lo que se vería como mediante la fórmula:
|
Ejemplo 2
Convertir -120 ° a radianes. Deje la respuesta en términos de π.
Solución :
Utilizando la fórmula:
y reducir a su mínima expresión da:
Sin embargo, también puede darse cuenta de que 120 es 2 · 60. Desde 60 ° es
 radianes, entonces 120 es 2 persona radianes, entonces 120 es 2 persona  's o 's o 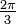 . Que sea negativo y tienes la respuesta, - . Que sea negativo y tienes la respuesta, - 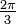 . . |
Ejemplo 3
Expresos
 en radianes medida en grados. en radianes medida en grados.
Solución :
|
Radianes, grados, y una calculadora [ editar ]
La mayoría de las calculadoras científicas y gráficas tienen un [MODE] ajuste que le permitirá a cualquiera convertir entre radianes y grados, o para encontrar aproximaciones para trig funciones utilizando medida. Es importante que si usted está utilizando su calculadora para estimar una función trigonométrica que usted sabe que el modo que esté utilizando. Mira la siguiente pantalla:
sin (30)
-.9880316241
Si ha introducido esta esperando encontrar el seno de 30 grados te darías cuenta basado en el último capítulo que algo está mal, ya que debería ser  . De hecho, como usted pudo haber sospechado, la calculadora interpreta esto como 30 radianes . En este caso, el cambio del modo de grados y recalculando damos el resultado esperado.
. De hecho, como usted pudo haber sospechado, la calculadora interpreta esto como 30 radianes . En este caso, el cambio del modo de grados y recalculando damos el resultado esperado.
 . De hecho, como usted pudo haber sospechado, la calculadora interpreta esto como 30 radianes . En este caso, el cambio del modo de grados y recalculando damos el resultado esperado.
. De hecho, como usted pudo haber sospechado, la calculadora interpreta esto como 30 radianes . En este caso, el cambio del modo de grados y recalculando damos el resultado esperado.
sin (30)
-.9880316241
sin (30)
0.5
Calculadoras científicas por lo general tienen una pantalla de 3 letras que muestra ya sea DEG o RAD para decirle que modo se encuentra. Compruebe siempre antes de calcular una relación trigonométrica!
Ejemplo 4
Encuentra la tangente
 . .
Solución :
En primer lugar, la culpa es tuya si está utilizando una calculadora para encontrar esta respuesta! Usted debe saber esto!
 es un 2 nd cuadrante de ángulo con un ángulo de referencia de es un 2 nd cuadrante de ángulo con un ángulo de referencia de  (45 grados). La tangente (45 grados). La tangente  es 1, y porque la tangente es negativa en el cuadrante II, la respuesta es -1. Para verificar esto en su calculadora, asegúrese de que el modo está en radianes , y evaluar la tangente es 1, y porque la tangente es negativa en el cuadrante II, la respuesta es -1. Para verificar esto en su calculadora, asegúrese de que el modo está en radianes , y evaluar la tangente  . .
tan (3π / 4)
-1
|
Ejemplo 5
Encuentra el valor de cos
 a cuatro decimales. a cuatro decimales.
Solución :
Una vez más, usted debe saber el exacto valor basado en su trabajo anterior.
 tiene un ángulo de referencia de tiene un ángulo de referencia de  (30 grados) y el signo de (30 grados) y el signo de  es es  . Debido a que . Debido a que  está en el 4 º cuadrante, el coseno es positivo y por lo que la respuesta exacta es está en el 4 º cuadrante, el coseno es positivo y por lo que la respuesta exacta es  . El uso de la calculadora Da: . El uso de la calculadora Da:
cos (11π / 6)
0,8660254038
Lo cual, cuando se redondea, es 0.8660. Usted puede verificar que de hecho es una muy buena aproximación de nuestra respuesta exacta utilizando la calculadora también.
cos (11π / 6)
0,8660254038
√ (3) / 2
0,8660254038
|
Ejemplo 6
Convertir 1 radian a medida en grados.
Solución :
Muchos estudiantes se acostumbran tanto a la utilización de π en radianes que piensan incorrectamente que 1 radian significa 1π radianes. Si bien es más conveniente y común para expresar radianes en términos de π, no perder de vista el hecho de que π radianes es en realidad un número! Se especifica un ángulo creado por una rotación de aproximadamente 3,14 longitudes de radio. Así 1 radián es una rotación creado por un arco que es sólo un único radio de longitud. Mirar hacia atrás en la Figura 1.1.¿Qué haría usted estima la medida en grados de este ángulo sea? Sin duda, es aguda y parece similar a un ángulo de 60 °. Para encontrar una aproximación más cercana, necesitaremos la fórmula y una calculadora.
Así 1 radian serían
 grados. El uso de cualquier calculadora científica o gráfica dará una aproximación razonable para esta medida en grados, aproximadamente 57,3 °. grados. El uso de cualquier calculadora científica o gráfica dará una aproximación razonable para esta medida en grados, aproximadamente 57,3 °.
180 / π
57.29577951
|
Ejemplo 7
Encuentra la medida en radianes de un ángulo agudo θ con un pecado θ = 0,7071.
Solución :
En primer lugar, es importante entender que la calculadora es muy probable que no le dará radianes en términos de π, pero una aproximación decimal en su lugar. En este caso es necesario utilizar la función seno inverso.
pecado -1(0.7071)
0,7853885734
Esta respuesta no puede mirar a todos conocemos, pero 0,7071 puede sonar familiar a usted. Es una aproximación
 . Así que, como ustedes saben, esto es realmente un ángulo de 45 °. Efectivamente, la evaluación . Así que, como ustedes saben, esto es realmente un ángulo de 45 °. Efectivamente, la evaluación  mostrará que la calculadora está dando su mejor aproximación de la medida en radianes. mostrará que la calculadora está dando su mejor aproximación de la medida en radianes.
pecado -1(0.7071)
0,7853885734
π / 4
0,7853981634
Si te molesta que no son exactamente lo mismo, bueno, se debe! Recuerde que 0,7071 es sólo una aproximación de
 , por lo que ya estamos empezando con un poco de error de redondeo. , por lo que ya estamos empezando con un poco de error de redondeo. |
Resumen de la lección [ editar ]
Los ángulos se pueden medir en grados o radianes. Un radián es el ángulo definido por una longitud de arco igual a la longitud del radio doblado alrededor del círculo. Una rotación completa alrededor de un círculo, o 360 ° es igual a 2π radianes. Para convertir de grados a radianes se utiliza la siguiente fórmula:
Para convertir de radianes a grados se convierte en la fórmula:
Al igual que el aprendizaje de un idioma extranjero en el que tienes que memorizar el vocabulario para tener éxito, será muy útil para que usted pueda entender y ser capaz de comunicarse en radianes si usted se familiarice con las medidas de los ángulos en radianes cuadrante (90 ° =  , 180 ° = π, 270 ° =
, 180 ° = π, 270 ° = 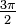 360 °, = 2π) y ángulos especiales (30 ° =
360 °, = 2π) y ángulos especiales (30 ° =  , 45 ° =
, 45 ° =  60 ° =
60 ° =  ).
).
 , 180 ° = π, 270 ° =
, 180 ° = π, 270 ° = 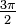 360 °, = 2π) y ángulos especiales (30 ° =
360 °, = 2π) y ángulos especiales (30 ° =  , 45 ° =
, 45 ° =  60 ° =
60 ° =  ).
).Preguntas de repaso [ editar ]
- La imagen de la derecha es un signo de una tienda que vende queso.
- (A) Calcule la medida en grados del ángulo del círculo que falta.
- (B) Convertir la medida en radianes.
- (C) ¿Cuál es la medida de arco de la parte del queso que queda?
- Convertir las siguientes medidas de grados a radianes. Dar respuestas exactas en términos de π, no decimal aproximaciones.
- (A) 240 °
- (b) 270 °
- (c) 315 °
- (d) -210 °
- (e) 120 °
- (F) 15 °
- (g) -450 °
- (h) 72 °
- (i) 720 °
- (j) 330 °
- Convertir las siguientes medidas en radianes a grados:
- (La)

- (B)
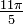
- (C)
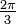
- (D)

- (E)

- (F)

- (G)

- (H)

- (Yo)

- (J)
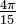
- (La)
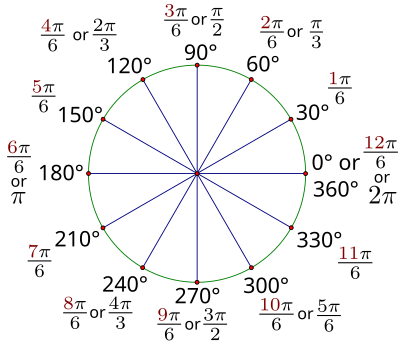
- El dibujo muestra todos los ángulos de cuadrante, así como aquellos con ángulos de referencia de 30 °, 45 °, y 60 °. En el círculo interior, etiquetar todos los ángulos con su medida en radianes en términos de π y en el círculo exterior, etiquetar todos los ángulos con su medida en grados.

- El uso de una calculadora, encuentre la medida en grados aproximada (en décimas) de cada ángulo expresado en radianes.
- (La)

- (B) 1 radian
- (C) 3 radianes
- (D)
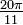
- (La)
- Gina quería calcular el coseno de 210 y obtuvo la respuesta siguiente en su calculadora:
- sin (210)0,4677185183
- (A) Escriba la respuesta correcta.
- (B) Explique lo que hizo mal.
- Complete el siguiente cuadro. Escriba sus respuestas en forma radical más simple.
X sin ( x ) cos ( x ) tan ( x ) 

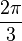

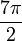
Revisar Respuestas [ editar ]
-
- (A) respuesta puede variar, pero 120 ° parece razonable.
- (B) Sobre la base de la respuesta en la parte a, la respuesta racional sería
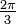
- (C) De nuevo, basado en una parte,

-
- (La)

- (B)
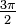
- (C)

- (D)

- (E)
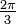
- (F)

- (G)

- (H)

- (Yo)
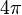
- (J)

- (La)
-
- (A) 90 °
- (b) 396 °
- (c) 120 °
- (d) 540 °
- (e) 630 °
- (F) 54 °
- (g) 75 °
- (h) -210 °
- (i) 1,440 °
- (j) 48 °

-
- (A) 154,3 °
- (b) 57.3 °
- (c) 171,9 °
- (d) 327,3 °
-
- (A) La respuesta correcta es
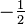
- (B) Su calculadora fue en el modo incorrecto y ella calcula el seno de 210 radianes .
- (A) La respuesta correcta es
X sin ( x ) cos ( x ) tan ( x ) 
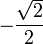
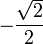





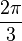




1 0 indefinido 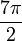
-1 0 indefinido



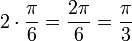

















 . Podría ser útil recordar que radianes casi siempre se expresa en términos de π. Si desea convertir de radianes a grados, desea que el π para cancelar cuando se multiplica, por lo que debe ser en el denominador.
. Podría ser útil recordar que radianes casi siempre se expresa en términos de π. Si desea convertir de radianes a grados, desea que el π para cancelar cuando se multiplica, por lo que debe ser en el denominador.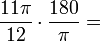
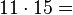


No hay comentarios:
Publicar un comentario