Funciones trigonométricas
En trigonometría, la secante hiperbólica de un número real , es una función hiperbólica definida como la inversa delcoseno hiperbólico. Se simboliza
, es una función hiperbólica definida como la inversa delcoseno hiperbólico. Se simboliza  y matemáticamente se sintetiza:
y matemáticamente se sintetiza:
 , es una función hiperbólica definida como la inversa delcoseno hiperbólico. Se simboliza
, es una función hiperbólica definida como la inversa delcoseno hiperbólico. Se simboliza  y matemáticamente se sintetiza:
y matemáticamente se sintetiza: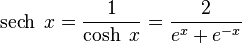
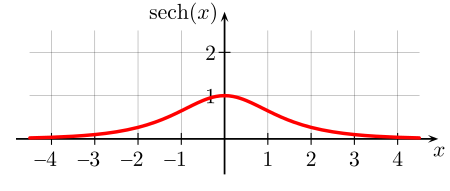 Gráfica de la función secante hiperbólica.
Gráfica de la función secante hiperbólica.- El dominio de la función está definido de
 a
a  y su codominio queda en el intervalo
y su codominio queda en el intervalo ![(0,1]](https://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) . La función presenta una asíntota horizontal en
. La función presenta una asíntota horizontal en 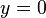 .Toma el nombre de hiperbólica por la oportunidad de poder utilizar u = acosht, v =bsenht, siendo t un número real, como ecuaciones paramétricas de una rama de la hipérbola de ecuación:1
.Toma el nombre de hiperbólica por la oportunidad de poder utilizar u = acosht, v =bsenht, siendo t un número real, como ecuaciones paramétricas de una rama de la hipérbola de ecuación:1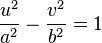
- En matemáticas el seno es una función continua y
 periódica es unafunción trascendente, su nombre se abrevia por sen.1 2 3
periódica es unafunción trascendente, su nombre se abrevia por sen.1 2 3
 En trigonometría, el seno de un ángulo
En trigonometría, el seno de un ángulo en un triángulo rectángulo de ángulo
en un triángulo rectángulo de ángulo  se define como la razón entre el catetoopuesto al ángulo y la hipotenusa:
se define como la razón entre el catetoopuesto al ángulo y la hipotenusa: O también como la ordenada correspondiente a un punto que pertenece a una circunferencia unitariacentrada en el origen (c=1):
O también como la ordenada correspondiente a un punto que pertenece a una circunferencia unitariacentrada en el origen (c=1):
Seno 
Gráfica de SenoDefinición sen x Dominio 
Imagen [-1,1] Cálculo infinitesimal Derivada cos x Función primitiva -cos x Función inversa asen x - El astrónomo y matemático hindú Aria Bhatta (476–550 d. C.) estudió el concepto de «seno» con el nombre de ardhá-jya,4 siendo ardhá:‘mitad, medio’, y jya: ‘cuerda’). Cuando los escritores árabes tradujeron estas obras científicas al árabe, se referían a este término sánscrito como jiba . Sin embargo, en el árabe escrito se omiten las vocales, por lo que el término quedó abreviado jb. Escritores posteriores que no sabían el origen extranjero de la palabra creyeron que jb era la abreviatura de jiab (que quiere decir ‘bahía’).A finales del siglo XII, el traductor italiano Gherardo de Cremona (1114-1187) tradujo estos escritos del árabe al latín reemplazó el insensato jiab por su contraparte latina sinus (‘hueco, cavidad, bahía’). Luego, ese sinus se convirtió en el español «seno».5Según otra explicación,[cita requerida] la cuerda de un círculo, se denomina en latín inscripta corda o simplemente inscripta. La mitad de dicha cuerda se llama semis inscríptae. Su abreviatura era s. ins., que terminó simplificada como sins. Para asemejarla a una palabra conocida del latín se la denominó sinus.
Relaciones trigonométricas
El seno puede relacionarse con otras funciones trigonométricas mediante el uso de identidades trigonométricas.[Expandir] 
Relación entre el seno y el coseno
La curva del coseno es la curva del seno desplazada a la izquierda dando lugar a la siguiente expresión:
a la izquierda dando lugar a la siguiente expresión:Seno de la suma de dos ángulos
[Expandir] 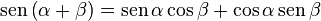

Seno del ángulo doble[editar]
[Expandir] 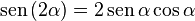
Seno del ángulo mitad[editar]
[Expandir] 
Suma de funciones como producto
Producto de funciones como suma[editar]
Seno en análisis matemático
Definición[editar]
La función seno puede definirse mediante la ecuación diferencial:si la condición inicial es (0,1) entonces su solución es e
e  .
.Derivada del seno[editar]
- Observación:
 .
.
Como serie de Taylor[editar]
El seno como Serie de Taylor en torno a a = 0 es:Con números complejos[editar]
También se puede definir de la forma:Donde e es la base del logaritmo natural, e i es la unidad de los números imaginarios.El seno en programación
Gran parte de los lenguajes de programación tienen la función seno en sus librerías, en caso de necesitar el seno de unos cuantos valores enteros es normal recurrir a vectores, eliminando así las llamadas a funciones frecuentemente lentas como el seno. Hay lenguajes en los que el ángulo recibido por la función es convertido a radianes.Algunas calculadoras aceptan el valor en grado sexagesimal, centesimales o radianes, es una opción activable mediante el teclado:Ejemplos:- Seno de 45 grados = 0,7071
- Seno de 45 radianes = 0,8509.
Obsérvese que la diferencia entre ambos valores resultantes podría pasar desapercibida. Es necesario, entonces, pasar los grados a radianes o viceversa. Nótese que el símbolo π es el número Pi. Ejemplo de conversiones:- Rad = Deg * π/180
- Deg = Rad * 180/π.
La comprobación del modo en curso de una calculadora se hace con valores conocidos: y 90º:
y 90º: en caso del modo de radianes activo.
en caso del modo de radianes activo. en caso del modo de grados sexagesimales activo.
en caso del modo de grados sexagesimales activo.
Representación gráfica
- opuesto al ángulo y la hipotenusa.Se denota por sen B.El seno de un ángulo en una circunferencia goniométrica es igual a la ordenada.
Signo del seno
Valores del seno de algunos ángulos
Relación entre el seno y el coseno
cos² α + sen² α = 1Ejemplo
Sabiendo que sen α = 3/5, y que 90º <α <180 calcular="" coseno="" de="" el="" p="">Seno del ángulo complementario
Seno del ángulo suplementario
Seno de ángulos que se diferencian en 180°
Seno del ángulo opuesto
Seno del ángulo negativo
Seno de un ángulo mayor de 360º
Seno de ángulos que diferencian en 90º
Seno de ángulos que suman en 270º
Seno de ángulos que se diferencian en 270º
Seno de una suma
Seno de una diferencia
Seno del ángulo doble
Seno del ángulo mitad
Transformación de una suma de senos en producto
Transformación de una diferencia de senos en producto
Transformación de un producto de senos en sumas




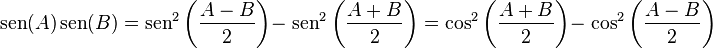





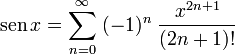
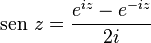


No hay comentarios:
Publicar un comentario