Funciones trigonométricas
En trigonometría, la cosecante hiperbólica de un número real  , es una función hiperbólica definida como la inversa del seno hiperbólico. Se simboliza
, es una función hiperbólica definida como la inversa del seno hiperbólico. Se simboliza  o
o  , y matemáticamente se sintetiza:
, y matemáticamente se sintetiza:
 , es una función hiperbólica definida como la inversa del seno hiperbólico. Se simboliza
, es una función hiperbólica definida como la inversa del seno hiperbólico. Se simboliza  o
o  , y matemáticamente se sintetiza:
, y matemáticamente se sintetiza: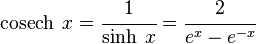
-
Gráfica de la función cosecante hiperbólica.
- FORMULAS BÁSICAS DE DERIVACIÓNFORMAS SIMPLESNºFORMAS COMPUESTAS12345678910111213141516171819202122232425262728293031
- REGLAS BÁSICAS DE DERIVACIÓN1ª) LA DERIVADA DE UNA CONSTANTE POR UNA FUNCIÓN es igual a la constante por la derivada de la función:2ªa) LA DERIVADA DE UNA SUMA DE FUNCIONES es igual a la suma de las derivadas de las funciones:2ªb) LA DERIVADA DE UNA DIFERENCIA DE FUNCIONES es igual a la diferencia de las derivadas de las funciones:3ª) LA DERIVADA DE UN PRODUCTO DE FUNCIONES es igual a la derivada de la primera función por la segunda función sin derivar más la primera función sin derivar por la derivada de la segunda función:4ª) LA DERIVADA DE UN COCIENTE DE FUNCIONES es igual a la derivada de la función del numerador por la función del denominador sin derivar, menos la función del numerador sin derivar por la derivada de la función del denominador, dividido todo ello por la función del denominador al cuadrado:5ª) LA DERIVADA DE UNA FUNCIÓN ELEVADA A OTRA es igual a la derivada de la expresión como exponencial más la derivada de la expresión como potencial:
 y
y 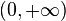 , es decir, sólo queda definida para todos los valores salvo x=0 e y=0.
, es decir, sólo queda definida para todos los valores salvo x=0 e y=0.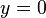 y otra
y otra  .
.
No hay comentarios:
Publicar un comentario