Funciones trigonométricas
En trigonometría, la arcosecante es la función inversa de lasecante de un ángulo. Se simboliza 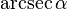 y su significado geométrico es el ángulo cuya secante es alfa.
y su significado geométrico es el ángulo cuya secante es alfa.
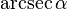 y su significado geométrico es el ángulo cuya secante es alfa.
y su significado geométrico es el ángulo cuya secante es alfa.
De esta definición, por tanto, podemos deducir expresiones equivalentes:
El dominio de definición de la función arcosecante está comprendido entre  y
y  o entre
o entre  y
y  . La función presenta una asíntota horizontal en
. La función presenta una asíntota horizontal en  , tal y como se deduce de la expresión:
, tal y como se deduce de la expresión:
 y
y  o entre
o entre  y
y  . La función presenta una asíntota horizontal en
. La función presenta una asíntota horizontal en  , tal y como se deduce de la expresión:
, tal y como se deduce de la expresión:
 Gráfica de la función arcosecante, con la función en color rojo y la asíntota marcada en color azul.
Gráfica de la función arcosecante, con la función en color rojo y la asíntota marcada en color azul.- La notación habitual de la función arcosecante es
 o bien sec-1 (leído como secante a la menos uno). Esta última notación no suele estar aconsejada debido a su ambigüedad, ya que es susceptible de ser confundida con una potencia de exponente -1, y su uso es habitual en Norte América y en las calculadoras de bolsillo.En el lenguaje LaTeX esta expresión se obtiene mediante el comando \arcsec.
o bien sec-1 (leído como secante a la menos uno). Esta última notación no suele estar aconsejada debido a su ambigüedad, ya que es susceptible de ser confundida con una potencia de exponente -1, y su uso es habitual en Norte América y en las calculadoras de bolsillo.En el lenguaje LaTeX esta expresión se obtiene mediante el comando \arcsec. - La derivada del arcosecante de una función es igual a la derivada de la función dividida por la función multiplicada por la raíz cuadrada del cuadrado de la función menos 1.
Las funciones trigonométricas inversas y sus derivadas
Conviene recordar que:
- a.
- Si una función es continua y estrictamente creciente (decreciente) en un intervalo, entonces posee función inversa la cual también es continua y estrictamente creciente (decreciente).
- b.
- Las funciones trigonométricas son periódicas por lo que la correspondencia entre la variable independiente y la dependiente no es "uno a uno".
De aquí se tiene que la inversa de una función trigonométrica no es una función, es una relación.
Sin embargo, si se restringe el dominio de una función trigonométrica se establece una relación biunívoca y la inversa de la función trigonométrica sí es una función.
Al considerar la gráfica de la función seno:
Se observa que en varios intervalos, por ejemplo:
![$\displaystyle{\left[\frac{-\pi}{2},\frac{\pi}{2}\right],\left[\frac{3\pi}{2},\frac{5\pi}{2}\right],\left[\frac{-5\pi}{2},\frac{-3\pi}{2}\right]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img698.gif) , etc, la función seno es continua y estrictamente creciente, por lo que podría escogerse alguno de ellos para definir la función inversa de la función seno. Usualmente se toma el intervalo
, etc, la función seno es continua y estrictamente creciente, por lo que podría escogerse alguno de ellos para definir la función inversa de la función seno. Usualmente se toma el intervalo ![$\displaystyle{\left[\frac{-\pi}{2},\frac{\pi}{2}\right]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img699.gif) . Luego, se define la función seno como:
. Luego, se define la función seno como:
![$\displaystyle{F=\left\{(x,y)/\; y=sen\;x, \;\;\mbox{con}\;\;
x\in \left[\frac{-\pi}{2},\frac{\pi}{2}\right] \;y\in [-1,1] \right\}}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img700.gif) La función
La función así definida es continua y estrictamente creciente en el intervalo
así definida es continua y estrictamente creciente en el intervalo![$\displaystyle{\left[\frac{-\pi}{2},\frac{\pi}{2}\right]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img699.gif) , por lo que existe una única función, definida en el intervalo
, por lo que existe una única función, definida en el intervalo ![$[-1,1]$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img701.gif) , llamada función seno inverso. Esta función, denotada arcsen, se define como sigue:
, llamada función seno inverso. Esta función, denotada arcsen, se define como sigue:  Se tiene entonces queLuego,
Se tiene entonces queLuego,![$\displaystyle{y=arc\;sen\;x \Leftrightarrow
x = sen\; y,
\;\;y\in \left[\frac{-\pi}{2},\frac{\pi}{2}\right] }$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img703.gif) .
. ![$arc\;sen\;r\;\; \mbox{con}\;\; r\in [-1,1]$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img704.gif) es el único número
es el único número ![$\displaystyle{t\in
\left[\frac{-\pi}{2},\frac{\pi}{2}\right]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img705.gif) para el cual
para el cual  .
.
Ejemplos:
La representación gráfica de la función seno y de la función arcoseno es la siguiente:a. 
b. 
c. 
d. 
Derivada de la función seno inverso
Como![$y=arc\;sen\;x \Leftrightarrow x= sen\; y,
\;\;\mbox{para}\;\; y\in
\displaystyle{\left[\frac{-\pi}{2},\frac{\pi}{2}\right], \;\;
x\in [-1,1]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img711.gif) , aplicando el teorema de la derivada de una función inversa se tiene que:
, aplicando el teorema de la derivada de una función inversa se tiene que:

Como , y
, y ![$\displaystyle{cos\;y \geq
0\;\;\mbox{para}\;\; y\in
\left[\frac{-\pi}{2},\frac{\pi}{2}\right]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img714.gif) entonces
entonces pues
pues  .
.
Luego:![$\displaystyle{D_{x}(arc\;sen\;x)=\frac{1}{\sqrt{1-x^{2}}}\;\;\mbox{para}\;\;
x\in ]-1,1[ }$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img717.gif)
En general![$\displaystyle{D_{x}(arc\;sen\;f(x))=\frac{f'(x)}{\sqrt{1-[f(x)]^{2}}},
f(x)\in]-1,1[}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img718.gif)
Ejemplos:
Determine si:
si:
Función coseno inversoa. 
b. 
Como en la función seno, la función coseno es continua y estrictamente decreciente en varios intervalos por ejemplo:![$[-2\pi,-\pi],[0,\pi],[2\pi,3\pi]$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img725.gif) , etc, por lo cual debe restringirse su dominio de tal forma que posea función inversa.
, etc, por lo cual debe restringirse su dominio de tal forma que posea función inversa.
Sea entonces la función tal que:
tal que:
![$F=\{(x,y)/\;y=cos\;x,\;\;\mbox{con}\;\;x\in [0,\pi],\;y\in
[-1,1] \}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img726.gif) La funciónSe define de la siguiente forma:
La funciónSe define de la siguiente forma: así definida es continua y estrictamente decreciente en el intervalo
así definida es continua y estrictamente decreciente en el intervalo ![$[0,\pi]$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img727.gif) , por lo que posee función inversa. Esta recibe el nombre de arco coseno, (o función coseno inverso), y se denota
, por lo que posee función inversa. Esta recibe el nombre de arco coseno, (o función coseno inverso), y se denota  .
.
![$\begin{array}{ccc}
arc\;cos: \;[-1,1] & \rightarrow & [0,\pi] \\
x & \rightarrow & arc\;cos\;x
\end{array}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img729.gif) Se tiene queLuego,
Se tiene queLuego,![$y=arc\;cos\;x\Leftrightarrow x=
cos\;y\;\;\mbox{con}\;\; y\in [0,\pi]$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img730.gif)
![$arc\;cos\;k \;\;\mbox{con}\;\; k\in [-1,1]$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img731.gif) es el único número
es el único número  con
con ![$\alpha \in [0,\pi]$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img732.gif) para el que
para el que 
Ejemplos:
La representación gráfica de la función coseno y la de la función arco coseno es la siguiente:- a.

b. 
c. 
d. 
Derivada de la función coseno inverso
Como![$y=arc\;cos\;x \Leftrightarrow x=cos\;y\;\;\mbox{para}\;\;
y\in[0,\pi],\; x\in[-1,1]$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img738.gif) , aplicando el teorema de la derivada de la función inversa se tiene que:
, aplicando el teorema de la derivada de la función inversa se tiene que:

Como , y
, y ![$\displaystyle{sen\;y \geq
0\;\;\mbox{para}\;\; y\in [0,\pi]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img740.gif) entonces
entonces pues
pues  .
.
Luego:![$\displaystyle{D_{x}(arc\;cos\;x)=\frac{-1}{\sqrt{1-x^{2}}}\;\;\mbox{con}\;\;
x\in ]-1,1[ }$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img743.gif)
En general![$\displaystyle{D_{x}(arc\;cos\;f(x))=\frac{-1}{\sqrt{1-[f(x)]^{2}}}\cdot
D_{x}f(x) ,
f(x)\in]-1,1[}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img744.gif)
Ejemplos:
Determine si:
si:
Función tangente inversaa. 
b. 
Igual que en los dos casos anteriores, vamos a restringir el dominio de la función tangente al intervalo![$\displaystyle{\left]\frac{-\pi}{2},\frac{\pi}{2}\right[}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img751.gif) , en el que es continua y estrictamente creciente, por lo que posee función inversa.
, en el que es continua y estrictamente creciente, por lo que posee función inversa.
Luego se define la función tangente como:
Se define la función tangente inversa, también llamada arco tangente, y denotada![$\displaystyle{G=\left\{(x,y)/\;y=tan\;x,\;\;\mbox{con}\;\;x\in
\left]\frac{-\pi}{2},\frac{\pi}{2}\right[,\;y\in
I\!\!R\right\}}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img752.gif)
 , como:
, como:
![$\begin{array}{ccc}
arc\;tan: I\!\!R& \rightarrow & \displaystyle{\left]\frac{-\pi}{2},\frac{\pi}{2}\right[} \\
x & \rightarrow & arc\;tan\;x
\end{array}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img754.gif) Se tiene queLuego,
Se tiene queLuego,![$y=arc\;tan\;x\Leftrightarrow x=
tan\;y\;\;\mbox{con}\;\; y\in \displaystyle{\left]\frac{-\pi}{2},\frac{\pi}{2}\right[}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img755.gif) ,
, 
 es el único número
es el único número  con
con ![$\alpha \in
\displaystyle{\left]\frac{-\pi}{2},\frac{\pi}{2}\right[}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img758.gif) para el que
para el que 
Ejemplos:
La representación gráfica de la función tangente y la de la función arcotangente es la siguiente:a. 
b. 
c. 
Además:



Derivada de la función arcotangente
Como![$y=arc\;tan\;x \Leftrightarrow x=tan\;y\;\;\mbox{para}\;\;
y\in\displaystyle{\left]\frac{-\pi}{2},\frac{\pi}{2}\right[},\;
x\in I\!\!R$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img765.gif) , aplicando el teorema de la derivada de la función inversa se tiene que:
, aplicando el teorema de la derivada de la función inversa se tiene que:
 ComoEn general
ComoEn general , y
, y  entonces
entonces  por lo que:
por lo que:
![$\displaystyle{D_{x}(arctan\;f(x))=\frac{1}{\sqrt{1+[f(x)]^{2}}}\cdot
D_{x}f(x)}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img771.gif)
Ejemplos:
Determine si:
si:
a. 
b. 
c. 
Función cotangente inversa
Para definir la función inversa de la función cotangente, vamos a restringir el dominio de ésta al intervalo![$]0,\pi[$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img778.gif) , en el que es continua y estrictamente decreciente, por lo que posee función inversa.
, en el que es continua y estrictamente decreciente, por lo que posee función inversa.
Se define función cotangente como:
![$\displaystyle{H=\left\{(x,y)/\;y=cot\;x,\;\;\mbox{con}\;\;x\in
]0,\pi[,\;\;y\in I\!\!R\right\}}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img779.gif) La función cotangente inversa, llamada también arco cotangente y denotada
La función cotangente inversa, llamada también arco cotangente y denotada , se define como:
, se define como: ![$\begin{array}{ccc}
arc\;cot:I\!\!R& \rightarrow & ]0,\pi[ \\
x & \rightarrow & cot\;x
\end{array}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img781.gif) Por la definición de la función arco cotangente se tiene que
Por la definición de la función arco cotangente se tiene que![$y=arc\;cot\;x\Leftrightarrow
cot\;y=x\;\;\mbox{con}\;\; y\in ]0,\pi[,\;\;x\in I\!\!R$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img782.gif) .Luego,Ejemplos:
.Luego,Ejemplos: es el único número
es el único número  con
con ![$\alpha \in ]0,\pi[$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img784.gif) para el que
para el que 
La representación gráfica de la función cotangente y la de la función arcocotangente es la siguiente:a. 
b. 
c.  Además:
Además:

Derivada de la función cotangente inversa
Como![$y=arc\;cot\;x \Leftrightarrow x=cot\;y\;\;\mbox{para}\;\;
y\in]0,\pi[,\; x\in I\!\!R$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img791.gif) , aplicando el teorema de la derivada de la función inversa se tiene que:
, aplicando el teorema de la derivada de la función inversa se tiene que:
 ComoEn general
ComoEn general , y
, y  entonces
entonces  por lo que:
por lo que:
![$\displaystyle{D_{x}(arc\;cot\;f(x))=\frac{-1}{1+[f(x)]^{2}}\cdot
D_{x}f(x)}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img797.gif)
Ejemplos:
Determine si:
si:
Función secante inversaa. 
b. 
Vamos a elegir como dominio de la función secante el intervalo de donde
de donde![$I=\displaystyle{\left[-\pi,\frac{-\pi}{2}\right]\;\;\cup\;\;\left[0,\frac{\pi}{2}\right]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img803.gif) , ya que en
, ya que en  la función secante es biunívoca y la derivada de la función inversa puede expresarse por medio de una sola fórmula.
la función secante es biunívoca y la derivada de la función inversa puede expresarse por medio de una sola fórmula.
La representación gráfica de la función secante en el intervalo señalado es el siguiente:
Como puede observarse, la función secante es continua en
 , siendo estrictamente decreciente en
, siendo estrictamente decreciente en  y estrictamente creciente en
y estrictamente creciente en  .
.
Existe por tanto la función secante inversa, llamada también arco secante y se denota definida por:
definida por:
 Por la definición de función arcosecante se tiene que:
Por la definición de función arcosecante se tiene que:
Luego,![$arc\;sec\;k \;\;\mbox{con}\;\; k\in
]-\infty,-1[\;\;\cup\;\;]1,+\infty[$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img809.gif) es el único número
es el único número  con
con![$\alpha \in
\displaystyle{\left[-\pi,\frac{-\pi}{2}\right]\;\;\cup\;\;\left[0,\frac{\pi}{2}\right]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img810.gif) tal que
tal que 
Ejemplos:
a. 
b. 
c. 

Note que:

Derivada de la función secante inversa
Como , utilizando el teorema de la derivada de la función inversa se obtiene que:
, utilizando el teorema de la derivada de la función inversa se obtiene que:
 ComoLuego
ComoLuego , y
, y  cuando
cuando ![$y \in
\displaystyle{\left[-\pi,\frac{-\pi}{2}\right]\;\;\cup\;\;\left[0,\frac{\pi}{2}\right]}
$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img821.gif) , entonces
, entonces pues
pues 

En general, si entonces
entonces 
Ejemplos:
Determine si:
si:
Nota:a. 
b. 
La función secante inversa también suele definirse por la siguiente igualdad: . En este caso
. En este caso 
Se deja como ejercicio para el estudiante que compruebe esta igualdad.
Función cosecante inversa
Tomaremos como dominio de la función cosecante el intervalo![$I=\displaystyle{\left[-\pi,\frac{-\pi}{2}\right]\;\;\cup\;\;\left[0,\frac{\pi}{2}\right]}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img803.gif) , en el que la función cosecante es biunívoca.
, en el que la función cosecante es biunívoca.
La representación gráfica de la función cosecante en el intervalo señalado es la siguiente:
Como puede observarse, la función cosecante es continua en
 , siendo estrictamente creciente en
, siendo estrictamente creciente en  y estrictamente decreciente en
y estrictamente decreciente en  .
.
Existe por tanto la función cosecante inversa, llamada también arco cosecante y que se denota definida por:
definida por:
 Por la definición de función arco cosecante se tiene que:
Por la definición de función arco cosecante se tiene que:
Luego, es el único número
es el único número  con
con tal que
tal que 
Ejemplos:
La representación gráfica de la función arco cosecante es la siguiente:a. 
b. 
c. 
d. 

Note que:

Derivada de la función cosecante inversa
Como , utilizando el teorema de la derivada de la función inversa se obtiene que:
, utilizando el teorema de la derivada de la función inversa se obtiene que:

Como , y
, y  para
para ![$y \in
\displaystyle{\left[-\pi,\frac{-\pi}{2}\right]\;\;\cup\;\;\left[0,\frac{\pi}{2}\right]}
$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img821.gif) , entonces
, entonces pues
pues 
Luego
En general, si entonces
entonces 
Ejemplos:
Determine si:
si:
Nota:a. ![$\displaystyle{h(x)=arccsc\;\sqrt[3]{x}}$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/img854.gif)
b. 
La función cosecante inversa también suele definirse por la siguiente igualdad: .
.
Además , igualdad que debe comprobar el estudiante como ejercicio.
, igualdad que debe comprobar el estudiante como ejercicio.
Verifiquemos que .
.

Luego , y se verifica la igualdad.
, y se verifica la igualdad.






No hay comentarios:
Publicar un comentario