Relacionar funciones trigonométricas
Las identidades recíprocas [ editar ]
El primer conjunto de identidades vamos a establecer son las identidades recíprocas. A recíproco de una fracción  es la fracción
es la fracción  . Es decir, nos encontramos con el recíproco de una fracción intercambiando el numerador y el denominador, o voltear la fracción. Las seis funciones trigonométricas se pueden agrupar en parejas como recíprocos.
. Es decir, nos encontramos con el recíproco de una fracción intercambiando el numerador y el denominador, o voltear la fracción. Las seis funciones trigonométricas se pueden agrupar en parejas como recíprocos.
 es la fracción
es la fracción  . Es decir, nos encontramos con el recíproco de una fracción intercambiando el numerador y el denominador, o voltear la fracción. Las seis funciones trigonométricas se pueden agrupar en parejas como recíprocos.
. Es decir, nos encontramos con el recíproco de una fracción intercambiando el numerador y el denominador, o voltear la fracción. Las seis funciones trigonométricas se pueden agrupar en parejas como recíprocos.
En primer lugar, tenga en cuenta la definición de la función seno para ángulos de rotación: sen θ =  . Consideremos ahora la función cosecante: csc θ =
. Consideremos ahora la función cosecante: csc θ =  . En la unidad de círculo, estos valores son pecado θ =
. En la unidad de círculo, estos valores son pecado θ =  = y y csc θ =
= y y csc θ =  . Estas dos funciones, por definición, son recíprocos. Por lo tanto el valor del seno de un ángulo siempre es el recíproco del valor cosecant, y viceversa. Por ejemplo, si sen θ =
. Estas dos funciones, por definición, son recíprocos. Por lo tanto el valor del seno de un ángulo siempre es el recíproco del valor cosecant, y viceversa. Por ejemplo, si sen θ =  , entonces csc θ =
, entonces csc θ =  = 2.
= 2.
 . Consideremos ahora la función cosecante: csc θ =
. Consideremos ahora la función cosecante: csc θ =  . En la unidad de círculo, estos valores son pecado θ =
. En la unidad de círculo, estos valores son pecado θ =  = y y csc θ =
= y y csc θ =  . Estas dos funciones, por definición, son recíprocos. Por lo tanto el valor del seno de un ángulo siempre es el recíproco del valor cosecant, y viceversa. Por ejemplo, si sen θ =
. Estas dos funciones, por definición, son recíprocos. Por lo tanto el valor del seno de un ángulo siempre es el recíproco del valor cosecant, y viceversa. Por ejemplo, si sen θ =  , entonces csc θ =
, entonces csc θ =  = 2.
= 2.
Análogamente, la función coseno y la función secante son recíprocos, y la función tangente y cotangente son recíprocos:
Podemos utilizar estas relaciones recíprocas para encontrar los valores de las funciones trigonométricas. La identidad fundamental derivada del teorema de Pitágoras 1 = sen 2x + cos 2 x puede tomar una gran cantidad de formas nuevas.
Ejemplo 1
Encuentra el valor de cada expresión usando una identidad recíproca.
a. cos θ = 0,3, sec θ =?
b. cuna θ =
 , cuna θ =? , cuna θ =?
Solución :
a. sec θ =

Estas funciones son recíprocos, así que si cos θ = 0.3, entonces sec θ =
 . Es más fácil encontrar el recíproco si expresamos los valores como fracciones: cos θ = 0,3 = . Es más fácil encontrar el recíproco si expresamos los valores como fracciones: cos θ = 0,3 = 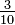 → sec θ = → sec θ =  . .
b. tan θ =
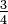
Estas funciones son recíprocos, y el de reciprocidad
 es es 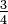 . . |
También podemos utilizar las relaciones recíprocas para determinar el dominio y el rango de funciones.
Dominio, rango, y los signos de Funciones [ editar ]
Mientras que las funciones trigonométricas pueden parecer muy diferentes de otras funciones que ha trabajado, que son, de hecho, al igual que cualquier otra función. Podemos pensar en una función trigonométrica en términos de "entrada" y "salida". La entrada es siempre un ángulo. La salida es una relación de lados de un triángulo. Si usted piensa acerca de las funciones trigonométricas de esta manera, se puede definir el dominio y el rango de cada función.
Consideremos primero las funciones seno y coseno. La entrada de cada una de estas funciones es siempre un ángulo, y como usted aprendió en el capítulo anterior, estos ángulos puede tomar cualquier valor de número real. Por lo tanto el seno y el coseno función tienen el mismo dominio, el conjunto de todos los números reales, R . Podemos determinar el rango de las funciones si pensamos en el hecho de que el seno de un ángulo es la y coordenada del punto en el lado terminal del ángulo de intersección con el círculo unitario. El coseno es la x coordenada de ese punto. Ahora recordamos que en el círculo unidad, definimos las funciones trigonométricas en términos de un triángulo con hipotenusa 1.
En este triángulo rectángulo, x y y son las longitudes de los catetos del triángulo, que deben tener longitudes de menos de 1, la longitud de la hipotenusa. Por lo tanto los intervalos de la función seno y coseno no incluyen valores mayor que uno. Los rangos de hacer, sin embargo, contienen valores negativos. Cualquier ángulo cuyo lado del terminal está en el tercer o cuarto cuadrante tendrá un negativo y coordenada, y cualquier ángulo cuyo lado del terminal está en el segundo o tercer cuadrante tendrán un negativo x coordenada.
En cualquier caso, el valor mínimo es -1. Por ejemplo, cos (180 °) = -1 y sin (270 °) = -1. Por lo tanto la función seno y coseno ambos tienen rango de -1 a 1.
La siguiente tabla resume los dominios y rangos de estas funciones:
Tabla 1.12 Dominio Alcance Seno θε ° -1 ≤ pecado theta ≤ 1 Coseno θε ° -1 ≤ cos theta ≤ 1
Conocer el dominio y el rango del coseno y la función seno puede ayudar a determinar el dominio y el rango de la función secante y cosecante. En primer lugar considerar las funciones seno y cosecante, que como vimos anteriormente, son recíprocos. La función cosecante se definirá siempre y cuando el valor del seno no es 0. Por lo tanto el dominio de la función cosecante excluye todos los ángulos con valor 0 sinusoidal, que son 0 °, 180 °, 360 °, etc.
En el capítulo 2 se analizarán las gráficas de estas funciones, que le ayudarán a ver por qué la relación recíproca resulta en un rango particular de la función cosecante. Aquí vamos a declarar este rango, y en las preguntas de repaso que exploraremos valores de la función u orden seno y cosecante comenzar a verificar este rango, así como el dominio y el rango de la función secante.
Tabla 1.13 Dominio Alcance Cosecante θε °, theta ≠ 0, 180, 360 ... csc theta ≤ -1 o csc theta ≥ 1 Secante θε °, theta ≠ 90, 270, 450 ... sec theta ≤ -1 o sec theta ≥ 1
Ahora vamos a considerar las funciones tangente y cotangente. La función tangente se define como  . Por lo tanto el dominio de esta función excluye ángulos para los que el par ordenado tiene una x coordenada de 0: 90 °, 270 °, etc. La función cotangente se define como
. Por lo tanto el dominio de esta función excluye ángulos para los que el par ordenado tiene una x coordenada de 0: 90 °, 270 °, etc. La función cotangente se define como  , por lo que el dominio de esta función excluirá ángulos para los que el par ordenado tiene una y coordenada de 0: 0 °, 180 °, 360 °, etc. Como usted aprenderá en el capítulo 3, cuando usted estudia las gráficas de estas funciones, no hay restricciones en los rangos.
, por lo que el dominio de esta función excluirá ángulos para los que el par ordenado tiene una y coordenada de 0: 0 °, 180 °, 360 °, etc. Como usted aprenderá en el capítulo 3, cuando usted estudia las gráficas de estas funciones, no hay restricciones en los rangos.
 . Por lo tanto el dominio de esta función excluye ángulos para los que el par ordenado tiene una x coordenada de 0: 90 °, 270 °, etc. La función cotangente se define como
. Por lo tanto el dominio de esta función excluye ángulos para los que el par ordenado tiene una x coordenada de 0: 90 °, 270 °, etc. La función cotangente se define como  , por lo que el dominio de esta función excluirá ángulos para los que el par ordenado tiene una y coordenada de 0: 0 °, 180 °, 360 °, etc. Como usted aprenderá en el capítulo 3, cuando usted estudia las gráficas de estas funciones, no hay restricciones en los rangos.
, por lo que el dominio de esta función excluirá ángulos para los que el par ordenado tiene una y coordenada de 0: 0 °, 180 °, 360 °, etc. Como usted aprenderá en el capítulo 3, cuando usted estudia las gráficas de estas funciones, no hay restricciones en los rangos.Tabla 1.14 Función Dominio Alcance Tangente θε °, theta ≠ 90, 270, 450 ... 
Cotangente θε °, theta ≠ 0, 180, 360 ... 
Conocer los rangos de estas funciones le muestra los valores que usted debe esperar cuando se determina el valor de una función trigonométrica de un ángulo. Sin embargo, para muchos de los problemas que tendrá que identificar el signo de la función de un ángulo: ¿Es positivo o negativo?
En la determinación de los rangos de las funciones seno y coseno anteriores, empezamos a categorizar los signos de estas funciones en términos de los cuadrantes en los que los ángulos mentira. La figura a continuación se resumen las indicaciones a los ángulos en los 4 cuadrantes.
Ejemplo 2
Indique el signo de cada expresión.
a. cos (100 °)
b. csc (220 °)
c. tan (370 °)
Solución :
a. El ángulo de 100 ° se encuentra en el segundo cuadrante. Por lo tanto la x coordenada es negativo y así cos (100 °) es negativo.
b. El ángulo de 220 ° es en el tercer cuadrante. Por lo tanto el y coordenada es negativo. Así que el seno y la cosecante son negativos.
c. El ángulo de 370 ° es en el primer cuadrante. Por lo tanto el valor de la tangente es positiva.
|
Hasta ahora hemos considerado las relaciones entre pares de funciones: las seis funciones trigonométricas se pueden agrupar en parejas como recíprocos. Ahora vamos a considerar las relaciones entre las tres funciones trigonométricas.
Cociente Identidades [ editar ]
Las definiciones de las funciones trigonométricas nos llevaron a las identidades recíprocas anteriores. También nos llevan a otro conjunto de identidades, las identidades de cociente.
Consideremos en primer lugar las funciones seno, coseno y tangente. Para ángulos de rotación (no necesariamente en el círculo unitario) estas funciones se definen como sigue:
Dadas estas definiciones, podemos demostrar que tan θ =  , siempre y cuando cos theta ≠ 0:
, siempre y cuando cos theta ≠ 0:
 , siempre y cuando cos theta ≠ 0:
, siempre y cuando cos theta ≠ 0:
La ecuación tan θ =  , por lo tanto es una identidad que podemos utilizar para encontrar el valor de la función tangente, dado el valor del seno y el coseno.
, por lo tanto es una identidad que podemos utilizar para encontrar el valor de la función tangente, dado el valor del seno y el coseno.
 , por lo tanto es una identidad que podemos utilizar para encontrar el valor de la función tangente, dado el valor del seno y el coseno.
, por lo tanto es una identidad que podemos utilizar para encontrar el valor de la función tangente, dado el valor del seno y el coseno.
Ejemplo 3
Si cos θ =
 y el pecado θ = y el pecado θ = 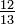 , ¿cuál es el valor de tan θ ? , ¿cuál es el valor de tan θ ?
Solución :
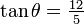 |
Ejemplo 4
Demostrar que cot θ =

Solución :
 |
Esta es también una identidad que puede utilizar para encontrar el valor de la función cotangente, valores dados de seno y el coseno. Tanto de las identidades cociente también será útil en el capítulo 3, en el que se demostrar otras identidades.
Identidades pitagóricas [ editar ]
El conjunto final de identidades que vamos a examinar en esta lección se llaman las identidades pitagóricas porque se basan en el Teorema de Pitágoras. En las lecciones anteriores hemos utilizado el teorema de Pitágoras para encontrar los lados de triángulos rectángulos. Considere una vez más la forma en que hemos definido las funciones trigonométricas en aspecto lección 4. Vamos a la unidad de círculo:
Las patas del triángulo rectángulo son x , y y . La hipotenusa es 1. Por lo tanto la ecuación siguiente es cierto para todas las x y y en el círculo unitario:
Ahora recordar que en el círculo unitario, cos θ = x y θ pecado = y . Por lo tanto la siguiente ecuación es una identidad:
Nota: Escribir el exponente 2 después de las cos y el pecado es la manera estándar de escribir exponentes. Hemos de tener en cuenta que cos 2 θ medios (cos θ ) 2 y el pecado2 θ medios (pecado θ ) 2 .
Podemos utilizar esta identidad para encontrar el valor de la función seno, dado el valor del coseno, y viceversa. También podemos usar esa información para encontrar identidades.
Ejemplo 5
Si cos θ =
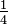 ¿cuál es el valor del pecado θ ? Suponga que θ es un ángulo en el primer cuadrante. ¿cuál es el valor del pecado θ ? Suponga que θ es un ángulo en el primer cuadrante.
Solución :

Recuerde que fue dado que θ es un ángulo en el primer cuadrante. Por tanto, el valor del seno es positivo, por lo que el pecado θ =
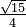 . . |
Ejemplo 6
Utilice la identidad cos 2 θ + sen 2 θ = 1 para demostrar que cot 2 θ + 1 = csc 2 θ .
Solución :
|
Resumen de la lección [ editar ]
En esta lección hemos examinado las relaciones entre dos o más de las funciones trigonométricas. Las identidades recíprocas nos dicen la relación entre pares de trig funciones que son recíprocos el uno del otro. Las identidades cociente nos dicen las relaciones entre las funciones de tres en tres: la función tangente es el cociente de las funciones seno y coseno, y la función cotangente es el recíproco de este cociente. Las identidades pitagóricas, que se basan en el teorema de Pitágoras, también nos dicen las relaciones entre las funciones de tres en tres. Cada identidad puede ser usado para encontrar los valores de las funciones trigonométricas, y así como para demostrar otras identidades, lo que será un foco de capítulo 3. También podemos utilizar identidades para determinar el dominio y el rango de funciones, que será útil en el capítulo 2, donde vamos a graficar las seis funciones trigonométricas.
Puntos a considerar [ editar ]
- ¿Cómo saber si una ecuación es una identidad? [Sugerencia: usted podría considerar el uso de una calculadora y graficar una función relacionada, o puede tratar de demostrar matemáticamente.]
- ¿Cómo se puede verificar el dominio o rango de una función?
Preguntas de repaso [ editar ]
- Utilice las identidades recíprocas para dar el valor de cada expresión.
- (A) s θ = 4, cos θ =?
- (B) el pecado θ =
 , csc θ =?
, csc θ =?
- En la lección, se dio como el rango de la función cosecante: csc theta ≤ -1 o csc theta ≥ 1.
- (A) Utilice una calculadora para rellenar la tabla de abajo. Los valores de la Ronda a 4 decimales.
- (B) Utilice los valores de la tabla de explicar con sus propias palabras lo que ocurre con los valores de la función cosecante como la medida del ángulo se aproxima a 0 grados.
- (C) Explique lo que este le informa acerca de la gama de la función cosecante.
- (D) Discuta cómo podría explorar más a fondo los valores del seno y cosecante para comprender mejor el rango de la función cosecante.
Tabla 1.15 Ángulo pecado csc 10 ° 5 ° 1 ° 0,5 ° 0.1 ° 0 ° -0.1 ° -0.5 ° -1 ° -5 ° -10 °
- En la lección se le dio el dominio de la función secante como: θε °, theta ≠ 90, 270, 450 ... Explicar por qué ciertos valores están excluidos del dominio.
- Estado del cuadrante en el que se encuentra cada ángulo, indicando el signo de cada expresión.
- (A) sen (80 °)
- (B) cos (200 °)
- (C) cuna (325 °)
- (D) tan (110 °)
- Si cos θ =
 y el pecado θ =
y el pecado θ =  , ¿cuál es el valor de tan θ ?
, ¿cuál es el valor de tan θ ? - Utilice identidades cociente de explicar por qué la tangente y la función cotangente tienen valores positivos para los ángulos en el tercer cuadrante.
- Si el pecado θ = 0.4, ¿cuál es el valor de cos θ ? Suponga que θ es un ángulo en el primer cuadrante.
- Si cot θ = 2, ¿cuál es el valor de csc θ ? Suponga que θ es un ángulo en el primer cuadrante.
- Demostrar que 1 + tan 2 θ = s 2 θ .
- Explicar por qué es necesario hacer constar el cuadrante en el que se encuentra el ángulo de problemas como # 7.
Revisar Respuestas [ editar ]
-
- (La)
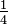
- (B)
 = 3
= 3
- (La)
-
- (La)
Tabla 1.15 Ángulo pecado csc 10 ° 0.1737 5,759 5 ° 0.0872 11.4737 1 ° 0.0175 57.2987 0,5 ° 0.0087 114.5930 0.1 ° 0.0018 572.9581 0 ° 0 indefinido -0.1 ° -0.0018 -572.9581 -0.5 ° -0.0087 -114.5930 -1 ° -0.0175 -57.2987 -5 ° -0.0872 -11.4737 -10 ° -0.1737 -5.759 - (B) A medida que el ángulo se hace más pequeño y más pequeño, los valores cosecante se hacen más grandes y más grandes.
- (C) El rango de la función cosecante no tiene un máximo, como la función seno. Los valores se hacen más grandes y más grande.
- (D) Las respuestas variarán. Por ejemplo, si nos fijamos en valores cercanos a 90 grados, veríamos los valores cosecante se hacen más pequeños y más pequeños, acercándose a 1.
- Los valores de 90, 270, 450, etc, están excluidos porque hacen que la función no definida.
-
- (A) Cuadrante 1; positivo
- (B) Cuadrante 3; negativo
- (C) Cuadrante 4; negativo
- (D) Cuadrante 2; negativo
 =
= 
- La relación de seno y el coseno será positivo en el tercer cuadrante porque seno y coseno son ambos negativos en el tercer cuadrante.
- cos theta ≈ 0.92
- csc θ = √5








- Usando las identidades de Pitágoras da como resultado una ecuación de segundo grado, que tendrá dos soluciones. Afirmando que el ángulo se encuentra en un cuadrante particular, le dice que la solución es el valor real de la expresión. En el # 7, el ángulo está en el primer cuadrante, por lo tanto seno y el coseno debe ser positivo.
Vocabulario [ editar ]
- dominio
- El dominio de una función es el conjunto de todos los de entrada ( x valores) para los que se define la función.
- identidad
- Una identidad es una ecuación que es siempre cierto, siempre y cuando se definen las variables y expresiones involucradas.
- cociente
- Un cociente es el resultado de la división. Una fracción es una representación de un cociente.
- alcance
- El rango de una función es el conjunto de todos los de salida ( Y valores).
- recíproca
- El recíproco de una fracción es la fracción obtenida intercambiando el numerador y el denominador. Es decir, si "da la vuelta sobre" una fracción, el resultado es el recíproco.

























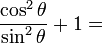






No hay comentarios:
Publicar un comentario