martes, 30 de junio de 2015

Trigonometría

Funciones trigonométricas

Las funciones hiperbólicas son unas funciones cuyas definiciones se basan en la función exponencial, conectando mediante operaciones racionales y son análogas a las funciones trigonométricas.1 Estas son:
Curvas de la funciones hiperbólicas sinh, cosh ytanh
Curvas de las funciones hiperbólicas csch, sech ycoth
\sinh(x) = \frac {e^{x} - e^{-x}} {2}
\cosh(x) = \frac {e^{x} + e^{-x}} {2}
\tanh(x) = \frac {\sinh(x)} {\cosh(x)}
y otras líneas:
\coth(x) = \frac {\cosh(x)} {\sinh(x)}
(cotangente hiperbólica)
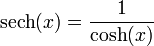
\mbox{sech}(x) = \frac {1} {\cosh(x)}
(secante hiperbólica)
\mbox{csch}(x) = \frac {1} {\sinh(x)}
(cosecante hiperbólica)







Las funciones trigonométricas sin(t) y cos(t) pueden ser las coordenadas cartesianas (x,y) de un punto P sobre la circunferencia unitariacentrada en el origen, donde es t el ángulo, medido en radianes, comprendido entre el semieje positivo X, y el segmento OP, según las siguientes igualdades:
\left \{ \begin{matrix} x(t) = \cos t \\ y(t) = \sin t \end{matrix} \right .
También puede interpretarse el parámetro t como la longitud del arco de circunferencia unitaria comprendido entre el punto (1,0) y el punto P, o como el doble del área del sector circular determinado por el semieje positivo X, el segmento OP y la circunferencia unitaria.
Animación de la representación del seno hiperbólico.
De modo análogo, podemos definir las funciones hiperbólicas, como las coordenadas cartesianas (x,y) de un punto P de la hipérbola equilátera, centrada en el origen, cuya ecuación es
\ x^2-y^2=1
siendo t el doble del área de la región comprendida entre el semieje positivo X, y el segmento OP y la hipérbola, según las siguientes igualdades:
\left \{ \begin{matrix} x(t) = \cosh t \\ y(t) = \sinh t \end{matrix} \right .
Sin embargo, también puede demostrarse que es válida la siguiente descripción de la hipérbola:
\ x(t) = \frac {e^{t} + e^{-t}} {2}
\ y(t) = \frac {e^{t} - e^{-t}} {2}
dado que
\ \left ( \frac {e^{t} + e^{-t}} {2} \right )^2 - \left ( \frac {e^{t} - e^{-t}} {2} \right )^2 = 1
De modo que el coseno hiperbólico y el seno hiperbólico admiten una representación en términos de funciones exponenciales de variable real:
\ \cosh(t) = \frac {e^{t} + e^{-t}} {2}
\ \sinh(t) = \frac {e^{t} - e^{-t}} {2}

Ecuación fundamental

\cosh^2(x) - \,\mathrm{sinh}^2(x) = 1 \,

Duplicación del argumento

Tenemos las siguientes fórmulas2 muy similares a sus correspondientes trigonométricas
\cosh(x+y) = \cosh(x)\cosh(y)+\sinh(x)\sinh(y)
que nos lleva a la siguiente relación:
\cosh(2x) = \cosh^2(x)+\,\mathrm{sinh}^2(x)
y por otra parte
\mathrm{sinh}(x+y) = \mathrm{sinh}(x)\cosh(y)+\mathrm{sinh}(y)\cosh(x)
que nos lleva a:
\mathrm{sinh}(2x) = 2\,\mathrm{sinh}(x)\cosh(x)
se tiene esta otra relación
\tanh(x + y)= \frac{\tanh (x) + \tanh (y)}{1 + \tanh (x) \tanh (y)}
que nos permite tener
\tanh(2x) = \frac{2\tanh x}{1 + \tanh^2 x}

Derivación e integración

\frac{d\ }{dx}(\cosh(x)) = \,\mathrm{sinh}\,(x)
\frac{d\ }{dx}(\,\mathrm{sinh}\,(x)) = \cosh(x)
\frac{d\ }{dx}(\,\tanh(x)) = \mathrm{sech}^2(x)
\frac{d\ }{dx}(\mathrm{coth}(x)) = -\mathrm{csch}^2(x)
\frac{d\ }{dx}(\mathrm{sech}(x)) = -\mathrm{sech}(x)\tanh(x)
\frac{d\ }{dx}(\mathrm{csch}(x)) = -\mathrm{csch}(x)\mathrm{coth}(x)
Además la integración al ser la operación inversa de la derivación es trivial en este caso.
La derivada de sinh(x) está dada por cosh(x) y la derivada de cosh(x) es sinh(x). El gráfico de la función cosh(x) se denomina catenaria.

Inversas de las funciones hiperbólicas y derivadas

Las funciones recíprocas y derivadas de las funciones hiperbólicas son:3 4
\begin{align} \mbox {arg sinh} (x) &= \ln \left(x + \sqrt{x^{2} + 1} \right) &\frac{d}{dx} (\mbox {arg sinh}(x) ) &= \frac{1}{ \sqrt{x^{2} + 1} } \\ \mbox {arg cosh} (x) &= \ln \left(x + \sqrt{x^{2} - 1} \right); x \ge 1 &\frac{d}{dx}(\mbox {arg cosh(x)})&=\frac{1}{\sqrt{x^{2} - 1}}; x > 1\\ \mbox {arg tanh} (x) &= \frac{1}{2}\ln \left( \frac{1 + x}{1 - x} \right); \left| x \right| < 1 &\frac{d}{dx}(\mbox {arg tanh(x)}) &= \frac{1}{1-x^2}; \left| x \right| < 1\\ \mbox {arg coth} (x) &= \frac{1}{2}\ln \left( \frac{x + 1}{x - 1} \right); \left| x \right| > 1 & \frac{d}{dx}(\mbox {arg coth(x)}) &= \frac{1}{1-x^2}; \left| x \right| > 1 \\ \mbox {arg sech} (x) &= \ln \left( \frac{1}{x} + \frac{\sqrt{1 - x^{2}}}{x} \right); 0 < x \le 1 & \frac{d}{dx}(\mbox {arg sech(x)})&=\frac{-1}{x\sqrt{1-x^2}}; 0 < x < 1 \\ \mbox {arg csch} (x) &= \ln \left( \frac{1}{x} + \frac{\sqrt{1 + x^{2}}}{\left| x \right|} \right); x \ne 0 & \frac{d}{dx}(\mbox {arg csch(x)}) &= \frac{-1}{\left| x \right| \sqrt{1+x^2}}; x \ne 0 \end{align}

Series de Taylor

Las series de Taylor de las funciones inversas de las funciones hiperbólicas vienen dadas por:
\mbox{arg sinh} (x) = x - \left( \frac {1} {2} \right) \frac {x^3} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^5} {5} - \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^7} {7} +\cdots =
\mbox{arg sinh} (x) = \sum_{n=0}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{2n+1}} {(2n+1)} , \left| x \right| < 1
\mbox{arg cosh} (x) = \ln 2x - (\left( \frac {1} {2} \right) \frac {x^{-2}} {2} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{-4}} {4} + \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{-6}} {6} +\cdots ) =
\mbox{arg cosh} (x) = \ln 2x - \sum_{n=1}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{-2n}} {(2n)} , x > 1
\mbox{arg tanh} (x) = x + \frac {x^3} {3} + \frac {x^5} {5} + \frac {x^7} {7} +\cdots =
\mbox{arg tanh} (x) = \sum_{n=0}^\infty \frac {x^{2n+1}} {(2n+1)} , \left| x \right| < 1
\mbox{arg csch} (x) = \mbox{arg sinh} (x^{-1}) = x^{-1} - \left( \frac {1} {2} \right) \frac {x^{-3}} {3} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{-5}} {5} - \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{-7}} {7} +\cdots =
\mbox{arg csch} (x) =\sum_{n=0}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{-(2n+1)}} {(2n+1)} , \left| x \right| < 1
\mbox{arg sech} (x) = \mbox{arg cosh} (x^{-1}) = \ln 2 - (\left( \frac {1} {2} \right) \frac {x^{2}} {2} + \left( \frac {1 \cdot 3} {2 \cdot 4} \right) \frac {x^{4}} {4} + \left( \frac {1 \cdot 3 \cdot 5} {2 \cdot 4 \cdot 6} \right) \frac {x^{6}} {6} +\cdots ) =
\mbox{arg sech} (x) =\ln 2 - \sum_{n=1}^\infty \left( \frac {(-1)^n(2n)!} {2^{2n}(n!)^2} \right) \frac {x^{2n}} {(2n)} , 0 < x \le 1
\mbox{arg coth} (x) = \mbox{arg tanh} (x^{-1}) = x^{-1} + \frac {x^{-3}} {3} + \frac {x^{-5}} {5} + \frac {x^{-7}} {7} +\cdots =
\mbox{arg coth} (x) =\sum_{n=0}^\infty \frac {x^{-(2n+1)}} {(2n+1)} , \left| x \right| > 1

Relación con la función exponencial

De la relación del coseno y seno hiperbólico se pueden derivar las siguientes relaciones:
e^x = \cosh x + \sinh x\!
y
e^{-x} = \cosh x - \sinh x.\!
Estas expresiones son análogas a las que están en términos de senos y cosenos, basadas en la fórmula de Euler, como suma de exponenciales complejos.


FUNCIONES HIPERBÓLICAS
  Las funciones  y = sinh x,  y = cosh x,  y = tanh x.
  En forma analítica, estas funciones pueden ser expresadas de forma análoga a las relaciones de Euler para las funciones circulares, esto es:  
    *  gráfica  de  y = sinh x
   
 La función senh x crece muy rápidamente hacia infinito , tanto en el eje positivo como en el negativo (hacia infinito negativo).

   *  gráfica  de  y = cosh x
 La función cosh x crece  muy rápidamente tanto en el eje positivo como el negativo hacia infinito positivo.

  *  gráfica  de  y = tanh x
 La función y = tanh x tiene por asíntota y=1 en el infinito positivo, y por asíntota y=-1 en el infinito negativo.

   Algunas relaciones:
     
   Las funciones hiperbólicas inversas:
  Las funciones inversas de sinh x, cosh x, tanh x, son, respectivamente llamadas "argumento seno hiperbólico", "argumento coseno hiperbólico" y "argumento tangente hiperbólica" (NOTA: algunos autores las llaman  "arco seno hiperbólico", "arco coseno hiperbólico" y "arco tangente hiperbólica"):
   y = arg sinh x    (función inversa de  y = sinh x) ,
   y = arg cosh x   (función inversa de  y = cosh x) ,
   y = arg tanh x    (función inversa de  y = tanh x) .
  De cualquier manera cada una de estas tres funciones tiene otra forma analítica más manejable:
   Por ejemplo, para la primera de ellas, podemos partir de:
despejar x:
por lo tanto, la función inversa del seno hiperbólico,  y = arg sinh x, puede también ser expresada:
en definitiva, las tres funciones hiperbólicas inversas son:
    
 Cuyas gráficas son:
   Observaciones:  
  *  y = arg sinh x se hace + (creciendo muy lentamente) en el infinito positivo, y se hace -, asimismo lentamente, en el infinito negativo.
  *  y = arg cosh x sólo esta definido para valores mayores o iguales a 1, se hace + (creciendo muy lentamente) en el infinito positivo.
  *  y = arg tanh x sólo esta definido para valores de x comprendidos entre -1 y +1, se hace + (creciendo rapidisimamente) en x=+1, y se hace -, asimismo rapidisimamente, en x=-1.
Publicado por en

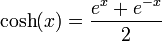
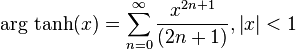
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)