Funciones trigonométricas
arcocoseno está definido como la función recíproca del cosenode un ángulo. Si tenemos:  , su significado geométrico es el arco cuyocoseno es alfa.
, su significado geométrico es el arco cuyocoseno es alfa.
 , su significado geométrico es el arco cuyocoseno es alfa.
, su significado geométrico es el arco cuyocoseno es alfa.
La función coseno no es biyectiva, por lo que no tiene recíproca. Es posible aplicarle una restricción del dominio de modo que se vuelva inyectiva y sobreyectiva. Por convención es preferible restringir el dominio del la función coseno al intervalo ![\left[-1, 1\right]](https://upload.wikimedia.org/math/f/f/1/ff1897f6d354c8079820a364c08e2f23.png) .La notación matemática del arcocoseno es arccos; es común la escritura ambiguacos-1. En diversos lenguajes de programación se suele utilizar la forma ACOS y ACS.
.La notación matemática del arcocoseno es arccos; es común la escritura ambiguacos-1. En diversos lenguajes de programación se suele utilizar la forma ACOS y ACS.
![\left[-1, 1\right]](https://upload.wikimedia.org/math/f/f/1/ff1897f6d354c8079820a364c08e2f23.png) .La notación matemática del arcocoseno es arccos; es común la escritura ambiguacos-1. En diversos lenguajes de programación se suele utilizar la forma ACOS y ACS.
.La notación matemática del arcocoseno es arccos; es común la escritura ambiguacos-1. En diversos lenguajes de programación se suele utilizar la forma ACOS y ACS.
El arcocoseno de una función continua es estrictamente decreciente, definida por todo el valor del intervalo ![\left[-1, 1\right]](https://upload.wikimedia.org/math/f/f/1/ff1897f6d354c8079820a364c08e2f23.png) :
:
![\left[-1, 1\right]](https://upload.wikimedia.org/math/f/f/1/ff1897f6d354c8079820a364c08e2f23.png) :
:
Su gráfico es simétrico respecto al punto  , siendo:
, siendo:
 , siendo:
, siendo:
La derivada del la función arcocoseno es
Por medio del la guía descrita simétrica vale la relación por argumentos negativos:
Es posible combinar la suma o diferencia de arcocoseno en una expresión donde el arcocoseno figura una rotación:

- El desarrollo en serie de potencias del arcocoseno viene dado por:Nótese que este desarrollo solo es válido cuando se expresa el ángulo en radianes.
- En un triángulo rectángulo, el arcocoseno equivale a la expresión en radianes del ángulo agudo correspondiente a la razón entre sucateto adyacente y la hipotenusa.
Función arcocoseno 
Gráfica de Función arcocosenoDefinición 
Tipo Trigonométrica inversa Dominio ![\textstyle [-1,1]](https://upload.wikimedia.org/math/8/5/a/85a1c5a07f21a9eebbfb1dca380f8d38.png)
Codominio ![\textstyle [0,\pi]](https://upload.wikimedia.org/math/c/9/a/c9a0c81b2547e7a52713e678c3f88f32.png)
Imagen ![\textstyle [0,\pi]](https://upload.wikimedia.org/math/c/9/a/c9a0c81b2547e7a52713e678c3f88f32.png)
Propiedades Estrictamente decreciente
Biyectiva en su dominioCálculo infinitesimal Derivada 
Función inversa ![\textstyle \cos(x) \quad x \in [0,\pi]](https://upload.wikimedia.org/math/1/3/f/13f428fc6df3035c9950ff20c0e006c7.png)
Funciones relacionadas arcoseno
arcotangente
- El arcocoseno es la función inversa del coseno. Es decir:Al ser el arcocoseno y el coseno funciones inversas, su composición es la identidad, es decir:Su abreviatura es arccos o cos-1.
Características del arcocoseno
- Dominio (x):
- Codominio (α):
- La función es continua y decreciente en todo el dominio.
- Derivada de la función arcocoseno:
- Integral de la función arcocoseno:
Arcocoseno de valores característicos
El arcocoseno de los valores más característicos es:Representación gráfica de la función arcocoseno
La gráfica de la función arcocoseno es simétrica a la de la función coseno respecto a la bisectriz del primer y tercer cuadrante (y=x). - Dominio (x):
- El arcocoseno es la función inversa o reciproca del coseno.y = arccos x
x = cos y
y es el arco cuyo coseno es el número x.Como el arcocoseno y el coseno son funciones inversas, su composición es la función identidad.arccos (cos x) = x.El arcocoseno también se puede expresar como: cos-1.Función arcocoseno
f(x) = arccosen x
Dominio: [-1, 1]Recorrido:Continua: (-1, 1)Decreciente: (-1, 1) - La derivada del arcocoseno de una función es igual a menos la derivada de la función dividida por la raíz cuadrada de uno menos el cuadrado de la función.
Ejemplos
Ejemplos
![\begin{array}{lccl}
\arccos: & [-1, 1] & \rightarrow & [0, \pi] \\
& x & \rightarrow & y = \arccos(x)
\end{array}](https://upload.wikimedia.org/math/f/d/0/fd0ab82d52bbc2524bd7e907fbd56cda.png)




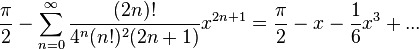
No hay comentarios:
Publicar un comentario