Altas Funciones Trigonometría Escuela / Definición trigonométricas
El Seno, coseno, tangente y funciones [ editar ]
Las tres primeras funciones trigonométricas vamos a trabajar son las funciones seno, coseno y tangente. Como se señaló anteriormente, los elementos de los dominios de estas funciones son ángulos. Podemos definir estas funciones en términos de un triángulo rectángulo: Los elementos de la gama de las funciones son relaciones particulares de los lados de los triángulos.
Definimos la función seno de la siguiente manera: Para un ángulo agudo x en un triángulo rectángulo, es el pecado x relación del lado opuesto del ángulo a la hipotenusa del triángulo. Por ejemplo, en el triángulo se muestra arriba, tenemos:
Dado que todos los triángulos rectángulos con el mismo ángulo agudo son similares, esta función es producirá la misma relación, no importa que el triángulo se utiliza. Por lo tanto, es una función bien definida.
Del mismo modo, el coseno de un ángulo se define como la relación del lado adyacente (junto a) el ángulo a la hipotenusa del triángulo. En el triángulo de arriba, tenemos:
Por último, la tangente de un ángulo se define como la relación del lado opuesto al ángulo hacia el lado adyacente al ángulo. En el triángulo de arriba, tenemos:
Hay algunas cosas importantes a tener en cuenta sobre la forma en que escribimos estas funciones. En primer lugar, tenga en cuenta que el pecado abreviaturas ( x ), cos ( x ) y tan ( x ) son como f ( x ). Simplifican reposar por tipos específicos de funciones. En segundo lugar, tener cuidado con cómo se pronuncia los nombres de las funciones.Cuando escribimos el pecado x todavía se pronunció sinusoidal , con una larga "i". Cuando escribimos cos x , todavía decimos co-sinusoidal. Y cuando escribimos tan x , todavía decimos tangente. (A veces la gente dice casualmente "cos" y "tan", sin embargo, no debería sorprender que el "pecado" siempre se pronuncia "sine"!)
Podemos utilizar estas definiciones para encontrar los seno, coseno, tangente y valores para los ángulos de un triángulo rectángulo.
Ejemplo 1
|
Una de las razones de que estas funciones nos ayudará a resolver problemas es que estas relaciones siempre serán los mismos, siempre y cuando los ángulos son iguales.Consideremos, por ejemplo, un triángulo similar al triángulo ABC .
Si CP tiene una longitud de 3, a continuación, otro AP del triángulo NAP es 6. Debido a NAP es similar a ABC , lado NP tiene longitud 8. Esto significa que la hipotenusa AN tiene longitud 10. (Podemos demostrar esto ya sea usando las proporciones de los triángulos semejantes , o utilizando el Teorema de Pitágoras.)
Si utilizamos triángulo NAP para encontrar el seno, coseno y tangente del ángulo A , obtenemos:
Ejemplo 2
Encuentra el pecado ( B ) utilizando el triángulo ABC y el triángulo del PAN .
Solución :
Usando triángulo ABC : el pecado B =

Usando triángulo PAN : el pecado B =
 = = |
Secante, cosecante y cotangente Funciones [ editar ]
Podemos definir tres más funciones también se basa en un triángulo rectángulo.
Tabla 1.9 Nombre de la función Definición Ejemplo Secante 
En el triángulo ABC , sec A = 
Cosecante 
En el triángulo ABC , csc A = 
Cotangente 
En el triángulo ABC , cuna Un = 
Ejemplo 3
Encuentra la secante, cosecante y cotangente del ángulo B .
Solución :
En primer lugar, tenemos que encontrar la longitud de la hipotenusa. Podemos hacer esto usando el teorema de Pitágoras:
Ahora podemos encontrar la secante, cosecante y cotangente del ángulo B :
|
Funciones trigonométricas de ángulos en posición estándar [ editar ]
Por encima, definimos las seis funciones trigonométricas de ángulos en triángulos rectángulos. También podemos definir las mismas funciones en cuanto a ángulos de rotación.Considere la posibilidad de un ángulo en posición estándar, cuyo equipo terminal de interseca un círculo de radio r . Podemos pensar en la radio que la hipotenusa de un triángulo rectángulo:
El punto ( x , y ), donde el lado del terminal del ángulo interseca el círculo nos dice las longitudes de los dos catetos del triángulo. Ahora, podemos definir las funciones trigonométricas en términos de x , y , y r :
Ahora podemos ampliar estas funciones para incluir ángulos no agudos.
Ejemplo 4
El punto (-3, 4) es un punto en el lado del terminal de un ángulo en posición estándar. Determinar los valores de las seis funciones trigonométricas del ángulo.
Solución :
Observe que el ángulo es de más de 90 grados, y que el lado terminal del ángulo se encuentra en el segundo cuadrante. Esto influirá en los signos de las funciones trigonométricas.
|
Observe que el valor de r depende de las coordenadas del punto dado. Siempre se puede encontrar el valor de r usando el Teorema de Pitágoras. Sin embargo, a menudo nos fijamos en los ángulos en un círculo con radio 1. Como se verá a continuación, hacer esto nos permite simplificar las definiciones de las funciones.
El Círculo Unidad [ editar ]
Considere un ángulo en posición estándar, de tal manera que el punto ( x , y ) en el lado del terminal del ángulo es un punto en un círculo con radio 1.
Este círculo se llama el círculo unidad . Con r = 1, podemos definir las funciones trigonométricas en el círculo unitario:
Nótese que en el círculo unidad, el seno y el coseno de un ángulo son las x y Y coordenadas del punto en el lado terminal del ángulo. Ahora podemos encontrar los valores de las funciones trigonométricas de cualquier ángulo de giro, incluso los ángulos de cuadrante, que no son ángulos en triángulos.
Podemos utilizar la figura de arriba para determinar los valores de las funciones trigonométricas de los ángulos de cuadrante. Por ejemplo, sen (90 °) = y = 1.
Ejemplo 5
Utilice la unidad círculo de arriba para encontrar cada valor:
a. cos 90 °
b. cuna 180 °
c. sec 0 °
Solución :
a. cos 90 ° = 0
b. Cuna de 180 ° es indefinido
c. seg 0 ° = 1
|
Hay varios ángulos importantes en el círculo unidad que va a trabajar mucho en su estudio de la trigonometría: 30 °, 45 ° y 60 °. Para encontrar los valores de las funciones trigonométricas de estos ángulos, lo que necesitamos saber los pares ordenados. Vamos a comenzar con 30 °.
El lado del terminal del ángulo interseca el círculo unidad en el punto  . (Va a probar esto en uno de los ejercicios de revisión.). Por lo tanto podemos encontrar los valores de cualquiera de las funciones trigonométricas de 30 °. Por ejemplo, el valor del coseno es la x coordenada, de modo cos (30 °) =
. (Va a probar esto en uno de los ejercicios de revisión.). Por lo tanto podemos encontrar los valores de cualquiera de las funciones trigonométricas de 30 °. Por ejemplo, el valor del coseno es la x coordenada, de modo cos (30 °) =  . Debido a que las coordenadas son fracciones, tenemos que hacer un poco más de trabajo con el fin de encontrar el valor de la tangente:
. Debido a que las coordenadas son fracciones, tenemos que hacer un poco más de trabajo con el fin de encontrar el valor de la tangente:
 . (Va a probar esto en uno de los ejercicios de revisión.). Por lo tanto podemos encontrar los valores de cualquiera de las funciones trigonométricas de 30 °. Por ejemplo, el valor del coseno es la x coordenada, de modo cos (30 °) =
. (Va a probar esto en uno de los ejercicios de revisión.). Por lo tanto podemos encontrar los valores de cualquiera de las funciones trigonométricas de 30 °. Por ejemplo, el valor del coseno es la x coordenada, de modo cos (30 °) =  . Debido a que las coordenadas son fracciones, tenemos que hacer un poco más de trabajo con el fin de encontrar el valor de la tangente:
. Debido a que las coordenadas son fracciones, tenemos que hacer un poco más de trabajo con el fin de encontrar el valor de la tangente:
En los ejercicios de revisión se encuentran los valores de los restantes cuatro funciones trigonométricas de este ángulo. La siguiente tabla resume los pares ordenados de 30 °, 45 ° y 60 ° en el círculo unidad.
Tabla 1.10 Ángulo x coordinar y coordenadas 30 ° 

45 ° 

60 ° 

Podemos usar estos valores para encontrar los valores de cualquiera de las seis funciones trigonométricas de estos ángulos.
Ejemplo 6
Encuentra el valor de cada función.
a. cos (45 °)
b. sen (60 °)
c. tan (45 °)
Solución :
a. cos (45 °) =

b. sen (60 °) =

c. tan (45 °) = 1
|
Resumen de la lección [ editar ]
En este capítulo hemos definido las seis funciones trigonométricas. Primero definimos las funciones de ángulos en triángulos rectángulos, y luego los definimos para ángulos de rotación. Se consideraron los ángulos formados cuando el lado terminal de un ángulo de intersección de un círculo de radio r , y luego nos hemos centrado en el círculo unidad, que tiene un radio 1. El círculo unidad se utiliza ampliamente en todo el resto del capítulo.
Puntos a considerar [ editar ]
- ¿Cómo es útil en la trigonometría el Teorema de Pitágoras?
- ¿Cómo pueden algunos valores de las funciones trigonométricas ser negativo? ¿Cómo es posible que algunos no están definidos?
- ¿Por qué es el círculo unidad y las funciones trigonométricas definidas en las que es útil, incluso cuando las hipotenusas de los triángulos en el problema no son 1?
Preguntas de repaso [ editar ]
- Encuentra los valores de las seis funciones trigonométricas de ángulo A .

- Considere triángulo FP a continuación.

- (A) Hallar la longitud de la hipotenusa.
- (B) Hallar los valores de las seis funciones trigonométricas de ángulo T .
- El punto (3, -4) es un punto en el lado terminal de un ángulo θ en la posición estándar.
- (A) Determinar el radio del círculo.
- (B) Determinar los valores de las seis funciones trigonométricas del ángulo.
- yo. El radio es 5.
- ii. Los valores son:
- El punto (-5, -12) es un punto en el lado terminal de un ángulo θ en la posición estándar.
- (A) Determinar el radio del círculo.
- (B) Determinar los valores de las seis funciones trigonométricas del ángulo.
- yo. El radio es 13.
- ii. Los valores son:
- El lado del terminal del ángulo de 270 ° se cruza con el círculo unidad en (0, -1). Utilice este par ordenado para encontrar las seis funciones trigonométricas de 270 °.
- En la lección que aprendió que el lado terminal del ángulo de 30 ° se cruza con el círculo unitario en el punto
 . Aquí podrás probar que esto es cierto.
. Aquí podrás probar que esto es cierto.
- (A) Explique por qué triángulo ABD es un triángulo equiangular. ¿Cuál es la medida del ángulo DAB ?
- (B) ¿Cuál es la longitud de BD ? Cómo lo sabes?
- (C) ¿Cuál es la longitud de BC y CD ? Cómo lo sabes?
- (D) Ahora a explicar por qué el par ordenado es

- (E) ¿Por qué te dice esto que el par ordenado de 60 ° es
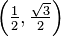
- En la lección que aprendió que el lado terminal del ángulo de 45 ° es
 . Utilice la siguiente figura y el Teorema de Pitágoras para demostrar que esto es cierto.
. Utilice la siguiente figura y el Teorema de Pitágoras para demostrar que esto es cierto.
- Estado de los valores de las seis funciones trigonométricas de 60º.
- En lo cuadrantes tendrá un ángulo en posición estándar tienen un valor de tangente positiva? Explica tu pensamiento.
- Dibuja el ángulo de 150 ° en el círculo unidad. ¿Cómo se relaciona este ángulo a 30 °? ¿Qué crees que el par ordenado es?
Revisar Respuestas [ editar ]






- La longitud de la hipotenusa es 17.
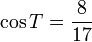

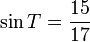






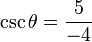






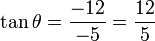




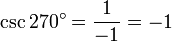


-
- (A) El triángulo es equiangular porque los tres ángulos miden 60 grados. Ángulo DAB mide 60 grados, ya que es la suma de dos ángulos de 30 grados.
- (B) BD tiene longitud 1, ya que es un lado de una equiangular, y por lo tanto triángulo equilátero.
- (C) BC y CD tienen cada uno de longitud
 , ya que son cada medio de BD . Este es el caso porque triángulo ABC y ADC son congruentes.
, ya que son cada medio de BD . Este es el caso porque triángulo ABC y ADC son congruentes. - (D) Podemos utilizar el teorema de Pitágoras para mostrar que la longitud de AC es
 . Si colocamos ángulo BAC como un ángulo en posición estándar, a continuación, AC y BC corresponden a la x y y coordenadas donde el lado del terminal del ángulo de intersección con el círculo unidad. Por lo tanto el par ordenado es
. Si colocamos ángulo BAC como un ángulo en posición estándar, a continuación, AC y BC corresponden a la x y y coordenadas donde el lado del terminal del ángulo de intersección con el círculo unidad. Por lo tanto el par ordenado es  .
. - (E) Si dibujamos el ángulo de 60 ° en posición estándar, también vamos a obtener un 30 - triángulo 90, pero las longitudes de los lados estaremos intercambiado - 60.Así que el par ordenado de 60 ° es
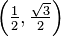 .
.

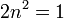




- Debido a que el ángulo está en el primer cuadrante, las x y Y coordenadas son positivas.






- Un ángulo en el primer cuadrante, como la tangente es el cociente de dos números positivos. Un ángulo en el tercer cuadrante, como la tangente en la relación de dos números negativos, que será positivo.
- El lado del terminal del ángulo es un reflejo de el lado del terminal de 30 °. A partir de esto, los estudiantes deben ver que el par ordenado es
 .
.
Vocabulario [ editar ]
- adyacente
- Un lado adyacente a un ángulo es el lado próximo al ángulo. En un triángulo rectángulo, es la pierna que está al lado del ángulo.
- hipotenusa
- La hipotenusa es el lado más largo de un triángulo rectángulo, opuesto al ángulo recto.
- pierna
- Las piernas de un triángulo rectángulo son los dos lados más cortos.
- Teorema De Pitágoras
- El teorema de Pitágoras establece la relación entre los lados de un triángulo rectángulo: Pierna 1 2 + Pierna 2 2 = Hipotenusa 2
- radio
- El radio de un círculo es la distancia desde el centro del círculo hasta el borde. El radio define el círculo.
- círculo unitario
- El círculo unidad es el círculo de radio 1 y centro (0, 0). La ecuación de la circunferencia unidad es x 2 + y 2 = 1










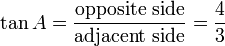


























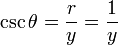

 es
es  , que no está definido.
, que no está definido. es
es 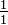 = 1.
= 1.

No hay comentarios:
Publicar un comentario