AMIGOS PARA SIEMPRE: Trigonometría

Funciones trigonométricas

En trigonometría, la arcocotangente es la función inversa de la cotangentede un ángulo dentro de un intervalo

(0,\pi)

. Se simboliza

\arccot \alpha\,

\operatorname{arcctg}\alpha\,

y su significado geométrico es el ángulo cuya cotangente es alfa.

y=\arccot(x) \longrightarrow x=\cot(y)

Y, teniendo en cuenta la relación entre la cotangente y la tangente, podemos establecer que:

\arccot(x)=\frac{\pi}{2} - \arctan(x)

Por tanto, por la propia definición de la función, su valor práctico más inmediato es el de despejar la longitud de un ángulo cuando conocemos la cotangente de éste.

Gráfica de la función arcocotangente.

La función está definida para todo número real ℝ, siendo, por tanto, sudominio de definición

(-\infty,\infty)

. El codominio de la función está acotado en el intervalo

[0, \pi]

. La arcocotangente es una función continua y estrictamente decreciente, definida para todos los números del conjunto real.

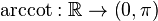\arccot: \mathbb R\rightarrow\left(0, \pi\right)

La función presenta límites en

\lim_{x\rightarrow+\infty}\arccot x=0

\lim_{x\rightarrow-\infty}\arccot x=\pi

La gráfica de la función es simétrica respecto al punto

\left(0,\frac\pi2\right)

, siendo entonces

\arccot x=\pi-\arccot\left(-x\right)

La derivada de la función arcocotangente es

\frac{d}{dx}\arccot x=-\frac1{1+x^2}

Comparación entre la gráfica de la función arcocotangente (en verde) y la gráfica de la función arcotangente (en rojo).

La notación habitual de la función arcocotangente es

\arccot(x)\,

o bien cot^-1 (leído como cotangente a la menos uno). Esta última notación no suele estar aconsejada debido a su ambigüedad, ya que es susceptible de ser confundida con una potencia de exponente -1, siendo su uso habitual en Norteamérica y en las calculadoras de bolsillo.

La derivada del arcotangente de una función es igual a menos la derivada de la función dividida por uno más el cuadrado de la función.

Derivada de la función inversa de una función

Dada una función

que tiene derivada no nula en

, si admite función inversa

en un cierto entorno de

, entonces

es derivable en

, siendo , es decir,

¨ Sólo es necesario tomar límites cuando

, ya que, si

, también

al ser f derivable, y, por tanto, continua en

, por lo cual

Ejemplo:

· 5.7.6. Derivada de la función arcoseno

¤ “La derivada de arcoseno de x es igual a la unidad partida por la raíz cuadrada de uno menos el cuadrado de x”

Incluyendo la Regla de la Cadena:

Ejemplos:

a) Si

, clara función compuesta de otras dos (arcoseno de la raíz cuadrada), su derivada será:

b) Si

, también composición de dos funciones: arcoseno de un cociente (o de una función racional fraccionaria), derivando obtendremos:

(este último paso, para mayor “claridad”)

· 5.7.7. Derivada de la función arcocoseno

¤ “La derivada de arcocoseno es la opuesta de la de arcoseno”

Incluyendo la Regla de la Cadena:

Ejemplos:

a) Si

, producto de una constante por la función compuesta arcocoseno del logaritmo neperiano, derivando tendremos:

b) Si

, función compuesta de tres funciones (arcocoseno de una exponencial natural de exponente polinómico), su derivada será:

· 5.7.8. Derivada de la función arcotangente

¤ “La derivada de arcotangente de x es igual a la unidad partida por uno más el cuadrado de x”

Incluyendo la Regla de la Cadena:

Ejemplos:

a) Si

, función compuesta de tres funciones (arcotangente de la raíz cuadrada de un polinomio), su derivada es:

b) Si

, arcotangente de una función racional fraccionaria (o de un cociente), derivando obtendremos:

c) Si

se trata de la composición de tres funciones:

. Es decir, se trata del arcotangente del coseno del seno. Por tanto, al derivar obtendremos

· 5.7.9. Derivada de la función arcocotangente

¤ “La derivada de arcocotangente es la opuesta de la de arcotangente”

Incluyendo la Regla de la Cadena:

Ejemplos:

a) Si

escribiremos primero

, y derivando ahora como producto de una constante por una función compuesta de tres funciones (arcocotangente de la raíz cuadrada de un polinomio) se tendrá:

b) Si

, producto de una constante por una función compuesta (arcocotangente de una exponencial de base 2), su derivada es:

c) Si

se trata del arcocotangente de una exponencial de base 7, luego derivando:

FUNCIONES TRIGONOMETRICAS INVERSAS

distintos en [- 1, 1].

la función seno. En estas condiciones se puede definir la aplicación inversa de f(x) = sen x, llamada «arco-seno» y que se simboliza por arc sen x.