La función cosecante (abreviado como csc o cosec) es la razón trigonométrica inversa del seno, o también su inverso multiplicativo:

Forma geométrica
Sabiendo que:A la vista de la figura, podemos ver que el ángulo de G es igual al ángulo de A, dado el triángulo GAF rectángulo en F, tenemos:Dado que F está en la circunferencia unitaria:Por lo tanto la cosecante será el segmento:Representación gráfica
Seno y cosecante de un ángulo
Partiendo de la definición de cosecante como la inversa del seno:Y conociendo la función seno previamente, podemos ver que para los valores en los que el seno vale cero, la cosecante se hace infinito, si la función seno tiende a cero desde valores negativos la cosecante tiende a: .mientras que cuando el seno tiende a cero desde valores positivos la cosecante tiende a:
.mientras que cuando el seno tiende a cero desde valores positivos la cosecante tiende a: .Cuando el seno del ángulo vale uno, su cosecante también vale uno, como se puede ver en la gráfica.
.Cuando el seno del ángulo vale uno, su cosecante también vale uno, como se puede ver en la gráfica.- La cosecante es la razón trigonométrica inversa del seno. Es el inverso multiplicativo del seno, es decir csc α · sen α=1.La cosecante del ángulo α de un triángulo rectángulo se define como la razónentre la hipotenusa (c) y el cateto opuesto (a).Sus abreviaturas son csc o cosec.
Cosecante de ángulos característicos
La cosecante de los ángulos más característicos es:Características de la cosecante
- Dominio:
- Codominio:
- Derivada de la función cosecante:
- Integral de la función cosecante:
Representación gráfica de la función cosecante
La función de la cosecante es periódica de período 360º (2π radianes), por lo que esta sección de la gráfica se repetirá en los diferentes períodos.Representación geométrica de la cosecante
Relaciones de la cosecante con las restantes razones trigonométricas
- Relación de la cosecante con el seno:
- Relación de la cosecante con el coseno:
- Relación de la cosecante con la tangente:
- Relación de la cosecante con la secante:
- Relación de la cosecante con la cotangente:
(1) Nota: el signo que corresponde en cada caso depende del cuadrante en que esté el ángulo.Cosecante del ángulo complementario, suplementario, conjugado y opuesto
- Cosecante del ángulo complementario:
- Cosecante del ángulo suplementario:
- Cosecante del ángulo conjugado:
- Cosecante del ángulo opuesto:
- Cosecante de ángulos que difieren 90º:
- Cosecante de ángulos que difieren 180º:
- Dominio:
- La cosecante es el inverso del seno, es decir, el cociente de la hipotenusa entre el cateto opuesto al ángulo.Gráficamente la representamos:Escribimos los valores de las medidas de las lineas presentes en la figura anterior relativas al angulo de 30º.








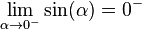
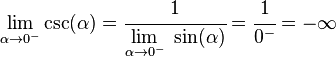


No hay comentarios:
Publicar un comentario