Para poder empezar con este tema Hay que recordar la definición de derivada:
Recordemos también que:
Teoremas
Teorema A :
Teorema B :
Teorema C :
Teorema D :
Teorema E :
Teorema F :
Derivada de seno
Sustituimos en la definicón de derivada y tenemos
f'(x) = \lim_{\Delta x\to 0}\frac{ sin(x+\Delta x)-sin(x)}{\Delta x}
Utilizamos la identidad de sin(a+b)=sin(a)cos(b)+cos(a)sin(b) por lo que
f'(x) = \lim_{\Delta x\to 0}\frac{ sin(x)cos(\Delta x)+cos(x)sin(\Delta x)-sin(x)}{\Delta x}
f'(x) = \lim_{\Delta x\to 0}\frac{ sin(x)[cos(\Delta x)-1]}{\Delta x}+ \lim_{\Delta x\to 0}\frac{ cos(x)sin(\Delta x)}{\Delta x}
f'(x) = -\sin x\,\lim_{\Delta x\to 0}\frac{ 1-cos(\Delta x)}{\Delta x}+ \cos x\,\lim_{\Delta x\to 0}\frac{ sin(\Delta x)}{\Delta x} \tag{1}
Sabemos que:
\lim_{\Delta x\to 0}\frac{ 1-cos(\Delta x)}{\Delta x}=0 \; \text{y} \; \lim_{\Delta x\to 0}\frac{ sin(\Delta x)}{\Delta x}=1
Sustituimos de lo anterior en la expresión (1)
f'(x)=-0(sin(x))+cos(x)(1)
f'(x)=cos(x)
Derivada de coseno
f(x)=cos(x)
Sustituimos en la definicion de derivada
f'(x)=\lim_{\Delta x\to 0}\frac{ cos(x+\Delta x)-cos(x)}{\Delta x}
Utilizamos la identidad cos(a+b)=cos(a)cos(b)-sin(a)sin(b), entonces tenemos que
f'(x) = \lim_{\Delta x\to 0}\frac{ cos(x)cos(\Delta x)-sin(x)sin(\Delta x)-cos(x)}{\Delta x}
f'(x) = \lim_{\Delta x\to 0}\frac{ cos(x)[cos(\Delta x)-1]}{\Delta x}- \lim_{\Delta x\to 0}\frac{ sin(x)sin(\Delta x)}{\Delta x}
f'(x) = -\cos x\lim_{\Delta x\to 0}\frac{ 1-cos(\Delta x)}{\Delta x}- \sin x\lim_{\Delta x\to 0}\frac{ sin(\Delta x)}{\Delta x}
Sabemos que:
f(x) = \lim_{\Delta x\to 0}\frac{ 1-cos(\Delta x)}{\Delta x}=0 y \lim_{\Delta x\to 0}\frac{ sin(\Delta x)}{\Delta x}=1
Sustituimos en la expresion anterior:
f'(x)=-0(cos(x))-(sin(x))(1)
f'(x)=-sin(x)
Ejemplo # 1
Ejemplo # 2
Ejemplo # 3
Ejemplo # 4
Introducción a la regla de la cadena:
Ejemplo # 5
Ejemplo # 6
Derivadas de funciones trigonométricas
Vamos a empezar por dar la derivada de
f(x) = sen x,
y después utilizarla para obtener las derivadas de las otras cinco funciones trigonométricas.
| Derivada de
sen x
La derivada de la función seno se da por
|
Eso es todo lo que hay que hacer!
Pregunta
¿De dónde vino esto?
RespuestaLo justificaremos al final de esta sección. (Si no puedes esperar, presiona la perla

para ir ahí ahora).
 Ejemplo 1
Ejemplo 1
Calcula
dy/dx
si:
|
| (a)
y = xsen x
| (b)
y = cosec x
| (c)
|
| (d)
y = sen(3x2 − 1)
|
Solución
(a) Una aplicación de la experimento mental de cálculo (EMC)* nos dice que
xsen x
es un producto;
Por lo tanto, por la regla del producto,
= (1)(
sen x) + (
x)(
cos x) =
sen x +
xcos x
(b) Reccuerda que en la sección 2 es así
Por lo tanto, por la regla del cociente,
=
| (0)(sen x) − (1)(cos x) |
| sen2x |
|
(recordemos que
sen2x
es sólo
(sen x)2
)
= − cotan xcosec x.
(de las identidades en la sección 2)
Nota que acabamos de obtener una derivada de las cinco funciones trigonométricas restantes. Faltan cuatro...
(c) Ya que la función dada es un cociente,
=
| (2x + 1)(sen x) − (x2 + x)(cos x) |
| sen2x |
|
,
y vamos a dejarlo así (no hay ninguna simplificación fácil de la respuesta).
(d) Aquí, una aplicación del EMC nos dice que y es el seno de una cantidad.
Ya que
La regla de cadena
( presione la perla para ir a un resumen del tema para una revisión rápida)
presione la perla para ir a un resumen del tema para una revisión rápida) nos dice que
por lo tanto
sen (3x2 − 1) =
cos (3x2 − 1)
(3x2 − 1)
= 6xcos(3x2 − 1)
(coloquemos el
6x
en frente para evitar confusión — ve mas abajo)
* Ve el ejemplo 6 en p. 258 en Cálculo Aplicado al Mundo Real, o p. 756 en Matemáticas Finitas y Cálculo Aplicado al Mundo Real. Alternativamente, presione aquí  para consultar el resumen del tema en línea, donde la EMC también se discute.
para consultar el resumen del tema en línea, donde la EMC también se discute.
Antes de seguir...
Trata de evitar escribir expresiones como
cos(3x2 − 1)(6x).
¿Esto significa
cos[(3x2 − 1)(6x)]
(el coseno de la cantidad
(3x2 − 1)(6x)),
o significa
[cos(3x2 − 1)](6x)
(el producto de
cos(3x 2 − 1)
y
6x)
?
Por esta razón colocamos el
6x
frente a la expresión del coseno.
Pregunta
¿Qué pasa con la derivada de la función coseno?
Respuesta
Utilicemos la identidad
de la sección 1, y sigamos el método del ejemplo 1(d) arriba: si
y = cos x = sen(π//2 − x),
entonces, usando la regla de cadena,
=
cos(
π//2 −
x)
(
π//2 −
x)
= (−1)cos(π//2 − x)
(ya que
π//2
es constante, y
d/dx(−x) = − 1
)
= − sen x
(usando la identidad
cos(π//2 − x) = sen x
)
Pregunta
¿Qué tal tres funciones trigonométricas restantes?
Respuesta
Ya que todas las demas se pueden expresar en términos de
sen x
y
cos x,
vamos a dejarlos para que tu los hagas en los ejercicios!
|
Regla original
|
Regla generalizada (Regla de cadena)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosec x = − cosec xcotan x
|
cosec u = − cosec u cotan u
|
 Ejemplo 2
Ejemplo 2
Determina la derivada de las siguientes funciones.
| (a)
f(x) = tan(x2 − 1)
| (b)
g(x) = cosec(e3x)
| (c)
h(x) = e−xsen(2x)
|
| (d)
r(x) = sen2x
| (e)
s(x) = sen(x2)
|
Solución
(a)Ya que
f(x)
es la
tan
de una cantidad, usamos la regla de cadena:
tan( x2 − 1) = sec2( x2 − 1)
(sustituyendo
u = x2 − 1)
|
|
= 2x sec2(x2 − 1).
|
(b) Ya que
g(x)
es el cosecante de una cantidad, usamos la regla
|
|
cosec u = − cosec u cotan u
|
|
|
|
cosec(e3x)
|
|
| |
= − 3e3x cosec(e3x)cotan(e3x).
| (la derivada de
e3x
es
3e3x)
|
(c) Ya que
h(x)
es el producto de
e−x
y
sen(2x),
usamos la regla del producto,
h ′(x)
|
=
|
(−e−x)sen(2x) + e−x
|
|
[sen(2x)]
|
|
|
=
|
|
(−e−x)sen(2x) + e−x
|
cos(2x)
|
|
[2x]
|
| (usando
d/dxsen u = cos u du/dx)
|
|
=
|
−e−xsen(2x) + 2e−xcos(2x).
|
(d) Recuerda que
sen2x = (sen x)2.
Así,
r(x)
es el cuadrado de la cantidad (particularmente, la cantidad de
sen x
). Por lo tanto, usamos la regla de la cadena para diferenciar el cuadrado de una cantidad,
|
|
[(sen x)2]
|
=
|
2(sen x)
|
|
| |
=
|
2sen xcos x.
|
(e) Nota la diferencia entre el
sen2x
y
sen(x2).
El primero es el cuadrado de
sen x,
mientras que el segundo es el
sen
de la cantidad
x2.
Ya que estamos diferenciando el segundo, usamos la regla de la cadena para diferenciar al seno de una cantidad:
Pregunta
Todavia hay algunos asuntos pendientes...
Respuesta
Efectivamente. Ahora nos motivará la fórmula que comenzó todo:
Vamos a hacer este cálculo partiendo de cero, usando la fórmula general par una derivada:
Ya que aquí,
f(x) = \sen x,
podemos escribir
\frac{d}{d} \sen(x) = \lim {h \to 0} \frac{\sen(x+h) - \sen(x)}{h}
| . . . . (I) |
Ahora utilizamos la fórmula para ampliar
\sen(x+h)
que aparecio en los ejercicio anteriores:
Sustituyendo esto en la formula (I) da
Agrupando los términos primeros y terceros, y factorizando el
\sen x
hacia afuera da
|
\frac{d}{d}
|
\sen(x) = \lim {h \to 0} \frac{\sen x (\cos h - 1) + \cos x \sen h}{h}
|
|
= \lim {h \to 0} \frac{\sen x (\cos h - 1)}{h} + \lim {h \to 0} \frac{\cos x \sen h}{h}
|
|
= \sen x\ \lim {h \to 0} \frac{(\cos h - 1)}{h} + \cos x\ \lim {h \to 0} \frac{\sen h}{h}
|
y
Por lo tanto,
 , es una función hiperbólica definida como la inversa de la tangente hiperbólica. Se simboliza
, es una función hiperbólica definida como la inversa de la tangente hiperbólica. Se simboliza 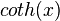 o
o 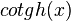 y matemáticamente se sintetiza:
y matemáticamente se sintetiza: , es una función hiperbólica definida como la inversa de la tangente hiperbólica. Se simboliza
, es una función hiperbólica definida como la inversa de la tangente hiperbólica. Se simboliza 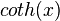 o
o 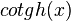 y matemáticamente se sintetiza:
y matemáticamente se sintetiza:
 Gráfica de la función cotangente hiperbólica.
Gráfica de la función cotangente hiperbólica. y
y 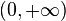 y su codominioqueda definido para el intervalo
y su codominioqueda definido para el intervalo  y
y  . La función presenta una asíntota horizontal en
. La función presenta una asíntota horizontal en  y en
y en  . A ambos lados de la asíntota nos encontramos una función monótona estrictamente decreciente.
. A ambos lados de la asíntota nos encontramos una función monótona estrictamente decreciente.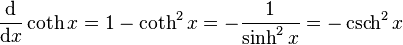

para ir ahí ahora).
Ejemplo 1
Calculady/dxsi:presione la perla para ir a un resumen del tema para una revisión rápida) nos dice que
para consultar el resumen del tema en línea, donde la EMC también se discute.
Antes de seguir...Trata de evitar escribir expresiones comocos(3x2 − 1)(6x).¿Esto significacos[(3x2 − 1)(6x)](el coseno de la cantidad(3x2 − 1)(6x)),o significa[cos(3x2 − 1)](6x)(el producto decos(3x 2 − 1)y6x)?Por esta razón colocamos el6xfrente a la expresión del coseno.Ejemplo 2
Determina la derivada de las siguientes funciones.para estos cálculos). Alternativamente, podemos tener una buena idea de lo que son estos dos límites por estimación numérica. Encontramos que:
\lim {h \to 0} \frac{(\cos h - 1)}{h} = 0y\lim {h \to 0} \frac{\sen h}{h} = 1Por lo tanto,\frac{d}{dx} \sen x = \sen x (0) + \cos x (1) = \cos x.
No hay comentarios:
Publicar un comentario