Trigonometría

Funciones trigonométricas

En trigonometría, elcoseno (abreviado cos) de un ángulo agudo en untriángulo rectángulo se define como la razón entre el cateto adyacente a dicho ángulo y lahipotenusa:

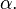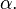En virtud del Teorema de Tales, este número no depende del triángulo rectángulo escogido y, por lo tanto, está bien construido y define una función del ángulo - ...........................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=a4a2618af3860d71b24d36162b524c06f242bc42&writer=rdf2latex&return_to=Coseno

El coseno del ángulo B es la razón entre el cateto contiguo al ángulo y la hipotenusa.

Se denota por cos B.

El coseno de un ángulo en una circunferencia goniométrica es igual a la abscisa.

Signo del coseno

Valores del coseno de algunos ángulos

Relación entre el seno y el coseno

cos² α + sen² α = 1

Ejemplo

Sabiendo que cos α = ¼ , y que  270º <α <360 calcular="" de="" el="" p="" seno="">

Coseno del ángulo complementario

Coseno del ángulo suplementario

Coseno de ángulos que se diferencian en 180°

Coseno del ángulo opuesto

Coseno del ángulo negativo

Coseno de un ángulo mayor de 360º

Coseno de ángulos que diferencian en 90º

Coseno de ángulos que suman en 270º

Coseno de ángulos que se diferencian en 270º

Coseno de una suma

Coseno de una diferencia

Coseno del ángulo doble

Coseno del ángulo mitad

Transformación de una suma de cosenos en producto

Transformación de una diferencia de cosenos en producto

Transformación de un producto de cosenos en sumas