Alta Trigonometría Escuela / Rotación de medición
Agudo, recto, obtuso y ángulos rectos [ editar ]
En general, los ángulos se clasifican por su tamaño. La siguiente tabla resume las categorías, lo que podría ser familiar de la lección anterior.
Tabla 1.8 Nombre Descripción Agudo Un ángulo cuya medida es menor que 90 grados. Derecho Un ángulo cuya medida es exactamente 90 grados. Obtuso Un ángulo cuya medida es de más de 90 grados, pero menos de 180 grados. Derecho Un ángulo cuya medida es exactamente 180 grados.
Usted debe asegurarse de que usted puede determinar visualmente qué categoría pertenece a un ángulo.
Ejemplo 1
Determinar si el ángulo es agudo, recto, obtuso o recto.
a.
b. c.
Solución :
a. Este ángulo es un ángulo agudo.
Si es difícil de categorizar el ángulo visual, se puede comparar a un ángulo recto. Hacer esto le ayudará a ver que el ángulo es menor que un ángulo recto.
b. Este ángulo es un ángulo obtuso.
Una vez más, se puede comparar el ángulo a ángulo recto, si es necesario.
c. Este ángulo es un ángulo recto.
Es importante tener en cuenta que por lo general un ángulo recto está marcado con un pequeño cuadrado.
|
También es importante tener en cuenta que se puede determinar la medida de un ángulo utilizando un transportador. Esta medida, por supuesto, ser una aproximación, ya que ningún transportador es perfecto y la medición persona puede no perfectamente alineación del transportador o mantenerla firme.
Ejemplo 2
|
Cuando se trabaja con ángulos medidos en grados, a menudo nos reportamos nuestras respuestas utilizando un decimal, por ejemplo 78,5 °. Sin embargo, en algunos contextos, los ángulos se miden utilizando partes fraccionarias.
Ángulos de medición [ editar ]
Ejemplo 3
Dos ruedas están en contacto directo. El radio de uno es 0,5 metros. El radio de la otra es de 1 metro. La más pequeña gira cuatro vueltas completas. ¿Cuántas rotaciones hace que la rueda más grande? ¿Cuántos grados hace la rueda más grande gire a través?
Solución :
Cada vez que la pequeña rueda gira una vez, toda su circunferencia pasa a lo largo de la rueda grande, C = 2π (0,5). Dado que la circunferencia de la rueda grande es 2π (1), la gran rueda gira medio camino alrededor. Así que si la pequeña rueda gira 4 veces, o 360 · 4 = 1440 ° la gran rueda gira 2 veces, o 360 · 2 = 720 °.
|
Podemos medir los ángulos de la misma forma en que medimos el tiempo. Un minuto es  de un grado. Un segundo es
de un grado. Un segundo es  de un minuto, por lo que es
de un minuto, por lo que es  de un grado. Por ejemplo, 48 ° 20'45 "es la forma en que escribimos 48 grados, 2 minutos y 45 segundos. Podemos escribir este ángulo usando la notación de fracción, así como la notación decimal:
de un grado. Por ejemplo, 48 ° 20'45 "es la forma en que escribimos 48 grados, 2 minutos y 45 segundos. Podemos escribir este ángulo usando la notación de fracción, así como la notación decimal:
 de un grado. Un segundo es
de un grado. Un segundo es  de un minuto, por lo que es
de un minuto, por lo que es  de un grado. Por ejemplo, 48 ° 20'45 "es la forma en que escribimos 48 grados, 2 minutos y 45 segundos. Podemos escribir este ángulo usando la notación de fracción, así como la notación decimal:
de un grado. Por ejemplo, 48 ° 20'45 "es la forma en que escribimos 48 grados, 2 minutos y 45 segundos. Podemos escribir este ángulo usando la notación de fracción, así como la notación decimal:
También podemos escribir un grado decimal usando grados, minutos y segundos. Por ejemplo, podemos reescribir 125.88 ° si escribimos la parte decimal como una fracción:
Ahora resuelva para x :
Ahora tenemos 125.88 ° = 125 ° 52.8 '. Tenemos que escribir 0,8 minutos como segundos:
Por lo tanto 125,88 ° = 125 ° 52'4.8 ".
Observe que el ángulo de 125,88 ° es un ángulo obtuso. Su medida es menor que 180 °. ¿Cómo se ve un ángulo como que es más de 180 °? Más de 360 °?
A continuación, aprenderá acerca de una manera particular para representar ángulos que le permitirán representa 180 °, 360 °, o cualquier otro ángulo.
Ángulos de rotación en la Norma Posición [ editar ]
Podemos utilizar nuestro conocimiento de gráficas para representar a cualquier ángulo. La siguiente figura muestra un ángulo en lo que se llama posición estándar .
La parte inicial de un ángulo en posición estándar está siempre en lo positivo x eje y. El lado del terminal siempre se encuentra con el lado inicial en el origen. Observe que la rotación va en un sentido contrario dirección. Esto significa que si giramos hacia la derecha , estamos generando un ángulo negativo. A continuación se presentan varios ejemplos de ángulos en posición estándar.
El ángulo de 90 grados es uno de cuatro de cuadrante ángulos. Un ángulo cuadrantal es aquella cuyo lado del terminal se encuentra en un eje. Junto con 90 °, 0 °, 180 ° y 270 ° son ángulos de cuadrante.
Estos ángulos se refieren como quadrantal porque cada ángulo define un cuadrante. Observe que sin la flecha que indica la rotación, 270 ° se ve como si se trata de un 90 °, definiendo el cuarto cuadrante. Note también que los 360 ° se vería igual que 0 °. La diferencia está en la acción de rotación. Esta idea de dos ángulos es en realidad el mismo ángulo se discute a continuación.
Coterminal Angles [ editar ]
Considere el ángulo de 30 °, en posición estándar.
Ahora considere el ángulo de 390 °. Podemos pensar en este ángulo como una rotación completa (360 °), más un adicional de 30 grados.
Observe que 390 ° se ve lo mismo que 30 °. Formalmente, se dice que los ángulos comparten el mismo lado del terminal. Por lo tanto llamamos a los ángulos co-terminal . No sólo son co-terminal de estos dos puntos de vista, pero hay un número infinito de ángulos que son co-terminal con estos dos ángulos. Por ejemplo, si rotamos otra 360 °, obtenemos el ángulo de 750 °. O, si creamos el ángulo en la dirección negativa (hacia la derecha), obtenemos el ángulo -330. Porque podemos girar en cualquier dirección, y podemos girar tantas veces como queramos, podemos seguir generando ángulos que son co-terminal con 30 °.
Ejemplo 3
¿Qué ángulos son co-terminal con 45 °?
a. -45 °
b. 405 °
c. -315 °
d. 135 °
Solución :
b. 405 ° y c. -315 ° son co-terminal con 45 °.
Observe que el lado terminal del primer ángulo, -45 °, se encuentra en el 4 º cuadrante. El último punto de vista, 135 ° se encuentra en el 2 º cuadrante. Luego tampoco ángulo es co-terminal con 45 °.
Consideremos ahora 405 °. Este es un giro completo, más un adicional de 45 grados. Así que este ángulo es co-terminal con 45 °. El ángulo de -315 ° pueden ser generados por girando en sentido horario. Para determinar dónde está el lado del terminal es, puede ser útil usar ángulos de cuadrante como marcadores. Por ejemplo, si se gira en sentido horario 90 grados 3 veces (para un total de 270 grados), el lado terminal del ángulo es en lo positivo y eje x. Para una rotación total de las agujas del reloj de 315 grados, tenemos 315-270 = 45 grados más para girar. Esto pone el lado del terminal del ángulo en la misma posición que 45 °.
|
Resumen de la lección [ editar ]
En esta lección hemos categorizado ángulos en función de su tamaño, y hemos ampliado nuestro conocimiento de ángulos para incluir ángulos de rotación. Hemos definido lo que significa para un ángulo de estar en posición estándar, y hemos mirado ángulos en posición estándar, incluyendo los ángulos de cuadrante. También hemos definido el concepto de ángulos co-terminal. Todas las ideas de esta lección se utilizará en la siguiente lección, para definir las funciones trigonométricas que son el foco de este capítulo.
Puntos a considerar [ editar ]
- ¿Cómo puede un ángulo verá exactamente el mismo que el otro punto de vista?
- ¿Dónde puede usted ver ángulos de giro en la vida real?
Preguntas de repaso [ editar ]
- Determinar si el ángulo es agudo, recto, obtuso o recto.
(a) (b)

- Calcule la medida del ángulo. Explica cómo aproximadas.
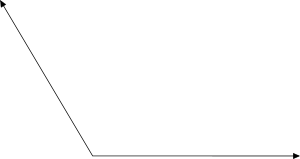
- Vuelva a escribir la medida de cada ángulo en grados, minutos y segundos.
- (A) 85,5 °
- (b) 12.15 °
- (c) 114,96 °
- Vuelva a escribir la medida de cada ángulo en grados decimales.
- (A) 54 ° 10'25 "
- (B) 17 ° 40'5 "
- Determine la medida del ángulo entre las manecillas del reloj en el momento dado.
- (A) 6:00
- (B) 03:00
- (C) 1:00
- A través de qué ángulo tiene el minutero de un reloj rote 12:00a.m.-1 a.m.?
- Un coche va alrededor de una curva circular de 90 grados en una pista de carreras. El diámetro de la rueda de un automóvil es 0,6 m. La distancia entre las ruedas es 2 m. El radio de la curva el coche está siguiendo es 100 m medidos en la rueda más cercana a la pista. ¿Cuál es la diferencia en el número de rotaciones que la rueda exterior debe girar a la comparación con la rueda interior?
- Estado de la medida de un ángulo que es co-terminal con 90 °.
- Nombra dos ángulos que son co-terminal con 120 °.
- (A) Un ángulo que es negativo.
- (B) un ángulo que es mayor que 360 °.
- Un auto de carreras va alrededor de una curva circular de 180 grados en una pista de carreras en un camino de la radio de 120 m. Sus ruedas delanteras y traseras tienen diferentes diámetros. Las ruedas delanteras son 0,6 m de diámetro. Las ruedas traseras son mucho más grandes; que tienen un diámetro de 1,8 m. Los ejes de las dos ruedas son 2 m de largo. ¿Qué rueda tiene más rotaciones que van alrededor de la curva. ¿Cuántos grados más ¿eso girar la rueda en comparación con la rueda que hace girar al menos por lo que la curva?
Revisar Respuestas [ editar ]
-
- (A) aguda
- (B) Recta
- El ángulo es de unos 120 grados. Puede aproximarse a la medida del ángulo utilizando un transportador, o mediante el uso de otros ángulos, tales como 90 y 30.
-
- (A) 85 ° 30 '
- (B) 12 ° 9 '
- (C) 114 ° 57'36 "
-
- (A) ≈ 54.236 °
- (B) ≈ 17.681 °
-
- (A) 180 °
- (b) 90 °
- (c) 30 °
- 360 °
- 5/6
- Las respuestas pueden variar. Ejemplos: 450 °, -270 °.
- Las respuestas pueden variar. Ejemplos: -240 °, 480 °.
- La rueda delantera gira más. Gira 100 revoluciones frente a 33,89 revoluciones de la rueda trasera, lo cual es una diferencia ~ 23.800 grados.
Vocabulario [ editar ]
- ángulo agudo
- Un ángulo agudo es un ángulo con medida entre 0 y 90 grados.
- ángulos co-terminal
- Los ángulos de rotación en la posición estándar son co-terminal de que comparten el mismo lado terminal.
- minutos
- Un minuto es
 de un grado.
de un grado. - ángulo obtuso
- Un ángulo obtuso es un ángulo con la medida entre 90 y 180 grados.
- transportador
- Un transportador es una herramienta que se utiliza para medir los ángulos.
- ángulo cuadrantal
- Un ángulo cuadrantal es un ángulo en posición estándar cuyo lado del terminal se encuentra en un eje.
- ángulo recto
- Un ángulo recto es un ángulo con medida exactamente 90 grados.
- segundos
- Un segundo es
 de un minuto, o
de un minuto, o  de un grado.
de un grado. - posición estándar
- Un ángulo en posición estándar tiene su lado inicial en el positivo x eje x, su vértice en el origen, y su lado del terminal en cualquier lugar en el plano. Un ángulo positivo significa una rotación en sentido antihorario. Un ángulo negativo significa un giro a la derecha.
- ángulo recto
- Un ángulo recto es un ángulo con medida 180 grados. Un ángulo recto hace una línea recta.







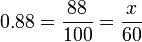


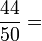



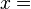





















No hay comentarios:
Publicar un comentario