martes, 30 de junio de 2015

Trigonometría

En trigonometría, la arcotangente se define como la función inversa de la tangentede un ángulo. Simbolizada:

y = \arctan \alpha \,

su significado geométrico es el arco

y

(en radianes) cuya tangente es

\alpha

La función tangente no es biyectiva, por lo que no tiene recíproca. Es posible aplicarle una restricción del dominio de modo que se vuelva inyectiva y sobreyectiva. Por convención es preferible restringir el dominio de la función tangente al intervalo abierto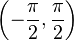

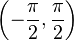\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)

Función arcotangente
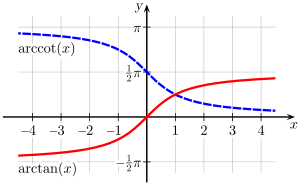Gráfica de Función arcotangente
Definición	$\textstyle f \mbox{ tal que } f(\tan(x))=x$ $\forall x\in (-\frac{\pi}2,\frac{\pi}2)$
Tipo	Trigonométrica inversa
Dominio	$(-\infty,+\infty)$
Codominio	$(-\infty,+\infty)$
Imagen	$\textstyle (-\frac{\pi}{2},\frac{\pi}{2})$
Cálculo infinitesimal
Derivada	$\frac{1}{x^2+1}$
Función inversa	$\textstyle \tan(x) \quad x \in (-\frac{\pi}{2},\frac{\pi}{2})$
Límites	$\lim_{x\to -\infty}\arctan(x)=-\frac{\pi}{2}\,$ $\lim_{x\to+\infty}\arctan(x)=\frac{\pi}{2}\,$
Funciones relacionadas	arcocoseno arcoseno

Como el resto de las funciones trigonométricas, es una función continua y derivable, de clase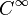

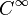C^\infty

(es decir, existen sus derivadas de todos los órdenes).

Es una función impar, o sea que

\arctan(-x)=-\arctan(x)

Algunos valores especiales

\arctan(0)=0

\arctan\left(\frac 1 \sqrt 3\right)=\frac \pi 6

\arctan(1)=\frac \pi 4

\arctan(\sqrt 3)=\frac \pi 3

Límites en infinito

\lim_{x\to\infty} \arctan(x) = \frac{\pi}{2}

\lim_{x\to-\infty} \arctan(x) = -\frac{\pi}{2}

Derivadas y crecimiento

(\arctan(x))' = \frac{1}{x^2+1}

En particular, resulta ser una función estrictamente creciente.

(\arctan(x))'' = -\frac{2x}{(x^2+1)^2}

, que es positivo en

\R^-

y negativo en

\R^+

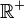Integral indefinida[editar]

Utilizando el método de integración por partes puede calcularse una función primitiva de

\arctan(x)

\int \arctan(x)\ dx=\int \arctan(x)\cdot 1\ dx= \arctan(x)\cdot x \ -\ \int x\cdot\frac 1 {x^2+1}dx= \arctan(x)\cdot x\ - \ \frac 1 2 \log(x^2+1) \ +\ C

Serie de Maclaurin[editar]

\arctan x = \sum^{\infin}_{n=0} \frac{(-1)^n}{2n+1} x^{2n+1}\quad\mbox{ para } \left| x \right| < 1.

En un triángulo rectángulo, la arcotangente equivale a la expresión en radianes del ángulo agudo correspondiente a la razón entre sucateto opuesto y su cateto adyacente.

Funciones Trigonométricas Básicas

Las funciones trigonométricas básicas, se pueden definir en función del triángulo rectángulo. Las funciones del ángulo θ del triángulo rectágulo siguiente se definen por:

Geometría Básica del Triángulo

Índice

HyperPhysics****HyperMath*****Trigonometría

M Olmo R Nave

Atrás

El Problema del Arco-Tangente

En el triángulo rectángulo que se muestra, se puede calcular el ángulo de

(varias notaciones para la misma función.) Un problema que surge en la suma de vectores cuando se obtiene las componentes del vector resultante, es que la función arco tangente en los lenguajes de calculadoras y ordenadores no distinguen el cuadrante del ángulo.

Geometría del Triángulo Rectángulo

Mas Detalles sobre el Problema del Arco Tangente

Índice

HyperPhysics****HyperMath*****Trigonometría

M Olmo R Nave

Atrás

Detalles Sobre el Problema del Arco Tangente

Cuando se calculen ángulos a partir de las coordenadas, debe prestarse cuidado debido al problema del arco tangente.

La arcotangente es la función inversa de la tangente. Es decir:

Al ser la arcotangente y la tangente funciones inversas, su composición es la identidad, es decir:

Composición de la arcotangente y la tangente.

Su abreviatura es arctan o tan^-1.

Características de la arcotangente

Dominio (x):
Codominio (α):
Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función tangenteno es inyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [-π/2,π/2] para que la función tangente sea biyectiva.
La función es continua y creciente en todo el dominio.
Derivada de la función arcotangente:
Integral de la función arcotangente:

Arcotangente de valores característicos

La arcotangente de los valores más característicos es:

Tabla del arcotangente de los valores más característicos (-1,-raiz(2)/2,-1/2,0,1/2,raiz(2)/2,1).

Representación gráfica de la función arcotangente

La gráfica de la función arcotangente es simétrica a la de la función tangente respecto a la bisectriz del primer y tercer cuadrante (y=x). Con la restricción al intervalo (-π/2, π/2) ambas funciones son crecientes y una inversa de la otra.

Gráfica de las funciones del seno y arcoseno, siendo simétricas respecto la recta y=x, siendo simétricas respecto la recta y=x.

AMIGOS PARA SIEMPRE

Páginas