Funciones trigonométricas de cualquier ángulo

Ángulos de referencia y ángulos en el Círculo Unidad [ editar ]

En la lección anterior, una de las preguntas de repaso que pidió considerar el ángulo de 150 °. Si graficamos este ángulo en posición estándar, vemos que el lado del terminal de este ángulo es un reflejo de el lado del terminal de 30 °, a través de la y eje x.

Observe que 150 ° hace un ángulo de 30 ° con el negativo x eje y. Por eso decimos que 30 ° es el ángulo de referencia de 150 °. Formalmente, el ángulo de referencia de un ángulo en posición estándar es el ángulo formado con la parte más cercana de la x eje y. Observe que 30 ° es el ángulo de referencia para muchos ángulos. Por ejemplo, es el ángulo de referencia para 210 ° y para -30 °.

En general, la identificación del ángulo de referencia para un ángulo le ayudará a determinar los valores de las funciones trigonométricas del ángulo.

Ejemplo 1

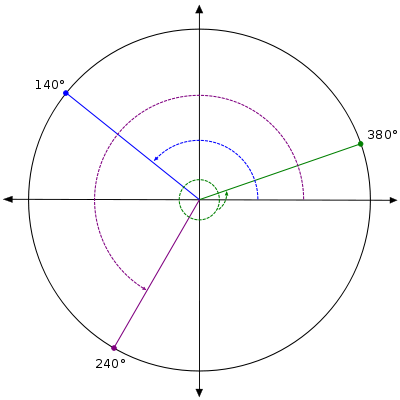
Grafique cada ángulo e identificar su ángulo de referencia.

a. 140 °

b. 240 °

c. 380 °

Solución :

a. 140 ° hace un ángulo de 40 ° con el x eje y. Por lo tanto el ángulo de referencia es 40 °.

b. 240 ° hace unos 60 ° con el x eje y. Por lo tanto el ángulo de referencia es 60 °.

c. 380 ° es una rotación completa de 360 °, más un adicional de 20 °. Así que este ángulo es co-terminal con 20 °, y 20 ° es su ángulo de referencia.

Si un ángulo tiene un ángulo de referencia de 30 °, 45 ° o 60 °, podemos identificar su par ordenado en el círculo unidad, y así podemos encontrar los valores de las seis funciones trigonométricas de ese ángulo. Por ejemplo, por encima de nosotros declarado que 150 ° tiene un ángulo de referencia de 30 °. Debido a su relación con el 30 °, el par ordenado es de 150 ° es

\ Left (- \ tfrac {\ sqrt {3}} {2}, \ tfrac {1} {2} \ right)

. Ahora podemos encontrar los valores de las seis funciones trigonométricas de 150 °:

$\ Cos (150 ^ \ circ) = x = \ frac {- \ sqrt {3}} {2}$	$\ Seg (150 ^ \ circ) = \ frac {1} {x} = \ frac {1} {\ frac {- \ sqrt {3}} {2}} = \ frac {-2} {\ sqrt {3 }}$
$\ Sin (150 ^ \ circ) = y = \ frac {1} {2}$	$\ Csc (150 ^ \ circ) = \ frac {1} {y} = \ frac {1} {\ frac {1} {2}} = 2$
$\ Tan (150 ^ \ circ) = \ frac {y} {x} = \ frac {\ frac {1} {2}} {\ frac {- \ sqrt {3}} {2}} = \ frac {1 } {- \ sqrt {3}}$	$\ Cuna (150 ^ \ circ) = \ frac {x} {y} = \ frac {\ frac {- \ sqrt {3}} {2}} {\ frac {1} {2}} = - \ sqrt { 3}$

Ejemplo 2

Encuentra el par ordenado de 240 ° y lo utilizan para encontrar el valor de sen 240 °.

Solución :

sen (240 °) =

\ Tfrac {- \ sqrt {3}} {2}

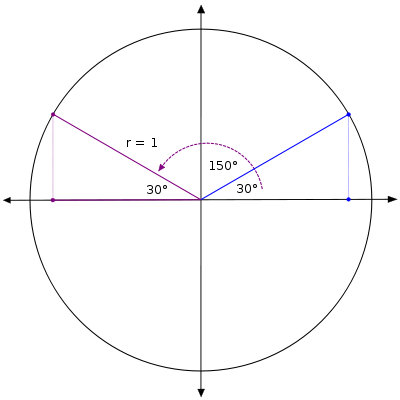
Como nos encontramos en el ejemplo 1, el ángulo de referencia para 240 ° es de 60 °. La siguiente figura muestra 60 ° y los otros tres ángulos en el círculo unitario que tienen 60 ° como ángulo de referencia.

El lado del terminal del ángulo de 240 ° representa un reflejo de el lado del terminal de 60 ° sobre ambos ejes. Así que las coordenadas del punto son

\ Left (- \ tfrac {1} {2}, - \ tfrac {\ sqrt {3}} {2} \ right)

. El ycoordenadas es el valor de seno, por lo que el pecado (240 °) =

\ Tfrac {- \ sqrt {3}} {2}

Así como la figura anterior muestra 60 ° y tres ángulos relacionados, podemos hacer gráficos similares para 30 ° y 45 °.

Ejemplo 3

Encontrar el valor de la cuna (300 °).

Solución :

cuna (300 °) =

- \ Tfrac {1} {\ sqrt {3}}

Usando el gráfico anterior, se encuentra que el par ordenado es

\ Left (\ tfrac {1} {2}, - \ tfrac {\ sqrt {3}} {2} \ right)

. Por lo tanto el valor cotangente es

\ Cuna (300 ^ \ circ) = \ frac {x} {y} = \ frac {\ frac {1} {2}} {- \ frac {\ sqrt {3}} {2}} = \ frac {1 } {2} \ cdot - \ frac {2} {\ sqrt {3}} = - \ frac {1} {\ sqrt {3}}

También podemos utilizar el concepto de un ángulo de referencia y los pares ordenados que hemos identificado para determinar los valores de las funciones trigonométricas para otros ángulos.

Funciones trigonométricas de ángulos negativos [ editar ]

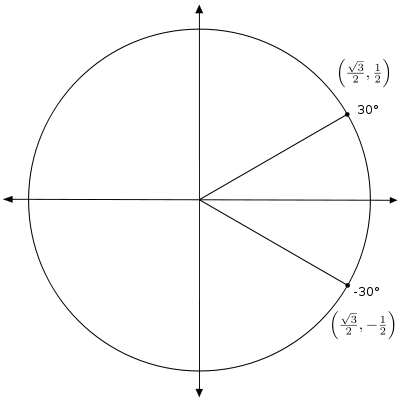
Recordemos que graficar un ángulo negativo significa girando en sentido horario. El siguiente gráfico muestra -30 °.

Observe que este ángulo es coterminal con 330 °. Así que el par ordenado es

\ Left (\ tfrac {\ sqrt {3}} {2}, - \ tfrac {1} {2} \ right)

. Podemos utilizar este par ordenado para encontrar los valores de cualquiera de las funciones trigonométricas de -30 °. Por ejemplo, cos (-30 °) = x =

\ Tfrac {\ sqrt {3}} {2}

En general, si un ángulo negativo tiene un ángulo de referencia de 30 °, 45 ° o 60 °, o si es un ángulo cuadrantal, podemos encontrar su par ordenado, y así podemos determinar los valores de cualquiera de las funciones trigonométricas de la ángulo.

Ejemplo 4

Encuentra el valor de cada expresión.

a. sin (-45 °)

b. seg (-300 °)

c. cos (-90 °)

Solución :

a. sin (-45 °) =

- \ Tfrac {\ sqrt {2}} {2}

-45 ° está en el 4 ^º cuadrante, y tiene un ángulo de referencia de 45 °. Es decir, este ángulo es coterminal con 315 °. Por lo tanto el par ordenado es

\ Left (\ tfrac {\ sqrt {2}} {2}, - \ tfrac {\ sqrt {2}} {2} \ right)

y el valor de seno es

- \ Tfrac {\ sqrt {2}} {2}

b. sec (-300 °) = 2

El ángulo de -300 ° está en el 1 ^er cuadrante y tiene un ángulo de referencia de 60 °. Es decir, este ángulo es coterminal con 60 °. Por lo tanto el par ordenado es

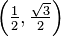\ Left (\ tfrac {1} {2}, \ tfrac {\ sqrt {3}} {2} \ right)

y el valor de la secante es

\ Tfrac {1} {x} = \ tfrac {1} {\ frac {1} {2}} =

c. cos (-90 °) = 0

El ángulo de -90 ° es coterminal con 270 °. Por lo tanto el par ordenado es (0, -1) y el valor del coseno es 0.

También podemos usar nuestro conocimiento de los ángulos de referencia y de pares ordenados para encontrar los valores de trig funciones de ángulos con medida superior a 360 grados.

Funciones trigonométricas de ángulos mayores de 360 grados [ editar ]

Considere el ángulo de 390 °. Como ha aprendido anteriormente, se puede pensar de este ángulo como una completa rotación de 360 grados, más un adicional de 30 grados.Por lo tanto 390 ° es coterminal con 30 °. Como se vio anteriormente, con ángulos negativos, esto significa que 390 ° tiene el mismo par ordenado como 30 °, y por lo que tiene los mismos valores trigonométricas. Por ejemplo, cos (390 °) = cos (30 °) =

\ Tfrac {\ sqrt {3}} {2} K

En general, si un ángulo cuya medida es mayor que 360 tiene un ángulo de referencia de 30 °, 45 ° o 60 °, o si es un ángulo cuadrantal, podemos encontrar su par ordenado, y así podemos encontrar los valores de cualquiera de las funciones trigonométricas del ángulo. El primer paso es determinar el ángulo de referencia.

Ejemplo 5

Encuentra el valor de cada expresión.

a. sen (420 °)

b. tan (840 °)

c. cos (540 °)

Solución :

a. sen (420 °) =

\ Tfrac {\ sqrt {3}} {2}

420 ° es una rotación completa de 360 grados, más un adicional de 60 grados. Por lo tanto el ángulo es coterminal con 60 °, y por lo que comparte el mismo par ordenado,

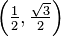\ Left (\ tfrac {1} {2}, \ tfrac {\ sqrt {3}} {2} \ right)

. El valor de seno es el y coordinar.

b. tan (840 °) = -√3

840 ° es dos vueltas completas, o 720 grados, más un adicional de 120 grados:

840 = 360 + 360 + 120

Por lo tanto 840 ° es coterminal con 120 °, por lo que el par ordenado es

\ Left (- \ tfrac {1} {2}, \ tfrac {\ sqrt {3}} {2} \ right)

. El valor de la tangente se puede encontrar lo siguiente:

\ Tan (840 ^ \ circ) = \ tan (120 ^ \ circ) = \ frac {y} {x} = \ frac {\ frac {\ sqrt {3}} {2}} {- \ frac {1} {2}} = \ frac {\ sqrt {3}} {2} \ cdot - \ frac {2} {1} = - \ sqrt {3}

c. cos (540 °) = -1

540 ° es una rotación completa de 360 grados, más un adicional de 180 grados. Por lo tanto el ángulo es coterminal con 180◦, y el par ordenado es (-1, 0). Así que el valor del coseno es -1.

Hasta ahora todos los ángulos que hemos trabajado son múltiplos de 30, 45, 60 y 90. A continuación encontrará los valores aproximados de las funciones trigonométricas de otros ángulos.

Los valores de funciones trigonométricas en los cuadros [ editar ]

A medida que trabaja a través de este capítulo, usted aprenderá acerca de las diferentes aplicaciones de las funciones trigonométricas. En muchos casos, usted tendrá que encontrar el valor de una función de un ángulo que no es necesariamente uno de los ángulos "especiales" que hemos trabajado hasta ahora. Tradicionalmente, los libros de texto han proporcionado a los estudiantes con las tablas que contienen los valores de las funciones trigonométricas. A continuación se muestra una tabla que proporciona valores aproximados del seno, coseno, tangente y valores de varios ángulos.

Tabla 1.11
Ángulo (°)	Coseno	Seno	Tangente
0	1,000	0,000	0,000
5	0.9962	0.0872	0.0875
10	0.9848	0.1736	0.1763
15	0.9659	0.2588	0.2679
20	0.9397	0.3420	0.3640
25	0.9063	0.4226	0.4663
30	0.8660	0.5000	0.5774
35	0.8192	0.5736	0.7002
40	0.7660	0.6428	0.8391
45	0.7071	0.7071	1.0000
50	0.6428	0.7660	1.1918
55	0.5736	0.8192	1.4281
60	0.5000	0.8660	1.7321
Sesenta y cinco	0.4226	0.9063	2.1445
70	0.3420	0.9397	2.7475
75	0.2588	0.9659	3.7321
80	0.1736	0.9848	5.6713
85	0.0872	0.9962	11.4301
90	0.0000	1.0000	indefinido
95	-0.0872	0.9962	-11.4301
100	-0.1736	0.9848	-5.6713
105	-0.2588	0.9659	-3.7321
110	-0.3420	0.9397	-2.7475
115	-0.4226	0.9063	-2.1445
120	-0.5000	0.8660	-1.7321
125	-0.5736	0.8192	-1.4281
130	-0.6428	0.7660	-1.1918
135	-0.7071	0.7071	-1.0000
140	-0.7660	0.6428	-0.8391
145	-0.8192	0.5736	-0.7002
150	-0.8660	0.5000	-0.5774
155	-0.9063	0.4226	-0.4663
160	-0.9397	0.3420	-0.3640
165	-0.9659	0.2588	-0.2679
170	-0.9848	0.1736	-0.1763
175	-0.9962	0.0872	-0.0875
180	-1.0000	0.0000	0.0000

Podemos utilizar la tabla para identificar valores aproximados.

Ejemplo 6

Encontrar el valor aproximado de cada expresión, utilizando la tabla anterior.

a. sen (130 °)

b. cos (15 °)

c. tan (50 °)

Solución :

a. sen (130 °) ≈ 0.7660

Podemos identificar el valor del seno mediante la búsqueda de la fila en la tabla de 130 grados. El valor de seno se encuentra en la tercera fila de la tabla. Tenga en cuenta que esto es un valor aproximado. Podemos evaluar la razonabilidad de este valor por pensar en un ángulo que está cerca de 130 grados, 120 grados. Sabemos que el par ordenado por 120 es

\ Left (- \ tfrac {1} {2}, \ tfrac {\ sqrt {3}} {2} \ right)

, por lo que el valor del seno es

\ Tfrac {\ sqrt {3}} {2}

≈ 0,8660, que también está en la mesa. Es razonable que sen (130 °) ≈ 0,7660, que es ligeramente menor que el valor del seno de 120 °, dado donde los lados terminales de estos ángulos se cruzan el círculo unidad.

b. cos (15 °) ≈ 0.9659

Podemos identificar este valor coseno mediante la búsqueda de la fila de 15 grados. El valor del coseno se encuentra en la segunda columna. Una vez más, podemos determinar si este valor es razonable considerando un ángulo cercano. 15 ° es entre 0 ° y 30 °, y su valor de coseno es entre los valores de coseno de estos dos ángulos.

c. tan (50 °) ≈ 1.1918

Podemos identificar este valor tangente mediante la búsqueda de la fila de 50 grados, y la lectura de la última columna de la tabla. En las preguntas de revisión, se le pedirá que explique por qué el valor de la tangente parece razonable.

Usando una calculadora para hallar valores [ editar ]

Si usted tiene una calculadora científica, se puede determinar el valor de cualquier función trigonométrica para cualquier ángulo. Aquí nos centraremos en el uso de una calculadora gráfica TI para encontrar valores.

En primer lugar, la calculadora tiene que estar en el "modo" correcto. En el capítulo 2 usted aprenderá sobre un sistema diferente para medir ángulos, conocidos como radianes.En este capítulo, estamos midiendo ángulos en grados. (Esto es análogo a la medición de la distancia en millas o en kilómetros. Es sólo un sistema diferente de medición.) Tenemos que asegurarnos de que la calculadora está trabajando en grados. Para ello, pulse [MODE] . Usted verá que la tercera fila dice Radian Degree. Si se pone de relieve Grado, usted está en el modo correcto. Si se pone de relieve Radian, desplácese hacia abajo para esta fila, desplácese a Grado, y pulse [ENTER] . Esto pondrá de relieve Grado. A continuación, pulse 2 ^nd[MODE] para volver a la pantalla principal.

Ahora se puede calcular cualquier valor. Por ejemplo, podemos verificar los valores de la tabla anterior. Para encontrar el pecado (130 °), pulse [SIN] [1] [3] [0] [ENTER] .La calculadora debe devolver el valor 0,7660444431.

Usted puede haber notado que la calculadora proporciona un "(" después de que el SIN. En el cálculo anterior, en realidad se puede dejar fuera de la ")". Sin embargo, en los cálculos más complicados, dejando fuera el cierre ")" puede crear problemas. Es una buena idea conseguir el hábito de paréntesis de cierre.

También puede utilizar una calculadora para encontrar los valores de las expresiones más complicadas.

Ejemplo 7

Usa una calculadora para encontrar un valor aproximado del pecado (25 °) + cos (25 °). Redondea tu respuesta a 4 decimales.

Solución :

sen (25 °) + cos (25 °) ≈ 1.3289

Para utilizar una calculadora gráfica TI, pulse [SIN] [25] [+] [COS] [2] [5] [ENTER] . La calculadora debe devolver el número 1,328926049. Esto se redondea a 1,3289.

Resumen de la lección [ editar ]

En esta lección hemos examinado la idea de que podemos encontrar una exacta o un valor aproximado de cada una de las seis funciones trigonométricas de cualquier ángulo.Comenzamos definiendo la idea de un ángulo de referencia, que es útil para encontrar el par ordenado para ciertos ángulos en el círculo unitario. Hemos encontrado valores exactos de las funciones trigonométricas para ángulos "especiales", incluyendo ángulos negativos y ángulos cuyas medidas son mayores que 360 grados. También hemos encontrado aproximaciones de valores para otros ángulos, mediante una tabla, y el uso de una calculadora. En las próximas lecciones, vamos a utilizar las ideas de esta lección para (1) examinar las relaciones entre las funciones trigonométricas y (2) se aplican las funciones trigonométricas a situaciones reales.

Puntos a considerar [ editar ]

¿Cuál es la diferencia entre la medida de un ángulo, y su ángulo de referencia? ¿En qué casos son estas medidas el mismo valor?
¿Qué ángulos tienen el mismo valor del coseno, o el mismo valor de seno? ¿Qué ángulos tienen coseno opuesto y valores de seno?

Preguntas de repaso [ editar ]

Indique el ángulo de referencia para cada ángulo.
(A) 190 °
(b) -60 °
(c) 1470 °
(d) -135 °
Indique el par ordenado para cada ángulo.
(A) 300 °
(b) -150 °
(c) 405 °
Encuentra el valor de cada expresión.
(A) sin (210 °)
(B) tan (270 °)
(C) csc (120 °)
Encuentra el valor de cada expresión.
(A) sen (510 °)
(B) cos (930 °)
(C) csc (405 °)
Encuentra el valor de cada expresión.
(A) cos (-150 °)
(B) tan (-45 °)
(C) sin (-240 °)
Utilice la tabla de la lección para encontrar un valor aproximado de cos (100 °).
Utilice la tabla en la lección para aproximarse a la medida de un ángulo cuyo valor seno es 0,2.
En el ejemplo 6c, encontramos que tan (50 °) ≈ 1,1918. Use su conocimiento de un ángulo especial para explicar por qué este valor es razonable.
Utilice una calculadora para hallar cada valor. Redondea a 4 decimales.
(A) sen (118 °)
(B) tan (55 °)
Utilice la tabla siguiente o una calculadora para explorar las relaciones de suma y de productos entre las funciones trigonométricas.
Considere las siguientes funciones:
f ( x ) = sin ( x + x ) y g ( x ) = sin ( x ) + sin ( x )
h ( x ) = sin ( x ) · sen ( x ) y j ( x ) = sin ( x ² )

¿Observa algún patrón en estas funciones? ¿Hay igualdades entre las funciones? ¿Se puede hacer una conjetura general sobre el pecado ( un ) + sen ( b ) y el pecado ( un + b ) para todos los valores de una , b ?
¿Qué pasa con el pecado ( un ) · sin ( un ) y el pecado ( un ² )?

a b ° pecado un pecado + b sin ( un + b )

10 30 0.6736 0.6428

20 60 1.2080 0.9848

55 78 1.7973 0.7314

122 25 1.2707 0.5446

200 75 0.6239 -0.9962
Utilice una calculadora o su conocimiento de ángulos especiales para rellenar los valores de la tabla, a continuación, utilizar los valores para hacer una conjetura sobre la relación entre (el pecado una ) ² y (cos una ) ² . Si utiliza una calculadora, redondo todos los valores a 4 decimales.

la (El pecadouna ) ² (Cosuna ) ²

0

25

45

80

90

120

250

a	b °	pecado un pecado + b	sin ( un + b )
10	30	0.6736	0.6428
20	60	1.2080	0.9848
55	78	1.7973	0.7314
122	25	1.2707	0.5446
200	75	0.6239	-0.9962

Revisar Respuestas [ editar ]

(A) 10 °
(b) 60 °
(c) 30 °
(d) 45 °
(La) $\ Left (\ tfrac {1} {2}, - \ tfrac {\ sqrt {3}} {2} \ right)$
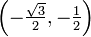
(B) $\ Left (- \ tfrac {\ sqrt {3}} {2}, - \ tfrac {1} {2} \ right)$
(C) $\ Left (\ tfrac {\ sqrt {2}} {2}, \ tfrac {\ sqrt {2}} {2} \ right)$
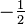
(La) $- \ Tfrac {1} {2}$
(B) indefinido
(C) $\ Tfrac {2} {\ sqrt {3}}$
(La) $\ Tfrac {1} {2}$
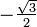
(B) $- \ Tfrac {\ sqrt {3}} {2}$
(C) √2
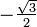
(La) $- \ Tfrac {\ sqrt {3}} {2}$
(B) -1
(C) $\ Tfrac {\ sqrt {3}} {2}$
-0.1736
Entre 165 y 160 grados.
Esto es razonable porque tan (45 °) = 1.
(A) 0,8828
(B) 1,4281
Conjetura: el pecado un pecado + b ≠ pecado ( un + b ).
Conjetura: (pecado una ) ² + (cos una ) ² = 1.

la (El pecadouna ) ² (Cosuna ) ²

0 0 1

25 0.1786 0.8216

45 0.5000 0.5000

80 0.9698 0.0302

90 1 0

120 0.7500 0.2500

250 0.8830 0.1170

la	(El pecadouna ) ²	(Cosuna ) ²
0	0	1
25	0.1786	0.8216
45	0.5000	0.5000
80	0.9698	0.0302
90	1	0
120	0.7500	0.2500
250	0.8830	0.1170

Vocabulario [ editar ]

ángulos coterminales: Dos ángulos en posición estándar son coterminal si comparten el mismo lado terminal.
ángulo de referencia: El ángulo de referencia de un ángulo en posición estándar es la medida del ángulo entre el lado del terminal y la parte más cercana de la x eje y.

AMIGOS PARA SIEMPRE

Páginas

martes, 30 de junio de 2015

Trigonometría

Funciones trigonométricas de cualquier ángulo

Ángulos de referencia y ángulos en el Círculo Unidad [ editar ]

Funciones trigonométricas de ángulos negativos [ editar ]

Funciones trigonométricas de ángulos mayores de 360 grados [ editar ]

Los valores de funciones trigonométricas en los cuadros [ editar ]

Usando una calculadora para hallar valores [ editar ]

Resumen de la lección [ editar ]

Puntos a considerar [ editar ]

Preguntas de repaso [ editar ]

Revisar Respuestas [ editar ]

Vocabulario [ editar ]

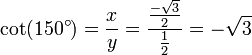
No hay comentarios:

Publicar un comentario

Datos personales

Archivo del blog