Resolver triángulos rectángulos [ editar ]
Usted puede utilizar su conocimiento del Teorema de Pitágoras y las seis funciones trigonométricas para resolver un triángulo rectángulo. Debido a que un triángulo rectángulo es un triángulo con un ángulo de 90 grados, la solución de un triángulo rectángulo requiere que usted encuentre las medidas de uno o ambos de los otros ángulos. Cómo resolver dependerá de la cantidad de información se da. Los siguientes ejemplos muestran dos situaciones: un triángulo falta un lado, y un triángulo de perderse dos lados.
Ejemplo 1
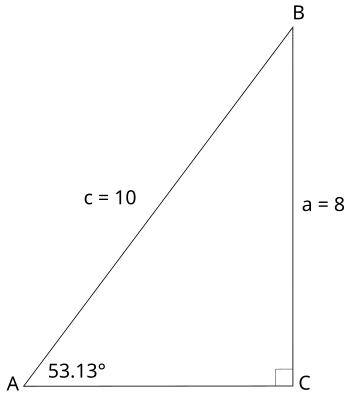
Resolver el triángulo que se muestra a continuación.
Solución :
Tenemos que encontrar las longitudes de todos los lados y las medidas de todos los ángulos. En este triángulo, dos de los tres lados se dan. Podemos encontrar la longitud del tercer lado usando el teorema de Pitágoras:
(Es posible que también ha reconocido la "terna pitagórica", 6, 8, 10, en lugar de llevar a cabo el Teorema de Pitágoras.)
También puede encontrar el tercer lado usando una relación trigonométrica. Tenga en cuenta que la parte que falta, b , es adyacente al ángulo A , y se da la hipotenusa. Por lo tanto podemos usar la función coseno para encontrar la longitud de b :
También podríamos utilizar la función tangente, como se le dio el lado opuesto. Puede parecer confuso que se puede encontrar el lado que falta en más de una forma. El punto es, sin embargo, no crear confusión, sino para mostrar que hay que mirar lo que la información no se encuentra, y elegir una estrategia. En general, cuando se necesita para identificar un lado del triángulo, puedes usar el Teorema de Pitágoras, o puede utilizar una relación trigonométrica.
Para resolver el triángulo de arriba, también tenemos que identificar las medidas de los tres ángulos. Se dan dos puntos de vista: 90 grados y 53,13 grados. Podemos encontrar el tercer ángulo utilizando la suma de los ángulos del triángulo:
|
Ahora vamos a considerar un triángulo que tiene dos lados que faltan.
Ejemplo 2
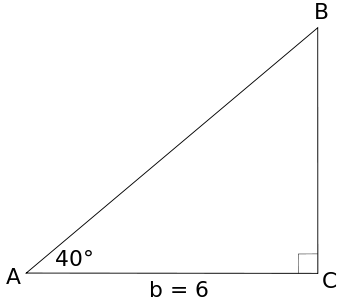
Resolver el triángulo que se muestra a continuación.
Solución : En este triángulo, tenemos que encontrar las longitudes de dos lados. Podemos encontrar la longitud de un lado utilizando una relación trig. Entonces podemos encontrar la longitud del tercer lado, ya sea utilizando una relación trig o el Teorema de Pitágoras.
Se nos da la medida del ángulo A , y la longitud del lado adyacente al ángulo A . Si queremos encontrar la longitud de la hipotenusa, c , podemos utilizar la relación coseno:
Si queremos encontrar la longitud del otro lado del triángulo, podemos utilizar la relación tangente. (¿Por qué es una idea mejor que utilizar el seno?)
Ahora sabemos que las longitudes de los tres lados de este triángulo. En las preguntas de revisión, usted verificar los valores de c y una utilizando el Teorema de Pitágoras.Aquí, para terminar de resolver el triángulo, sólo tenemos que encontrar la medida del ángulo B :
|
Nótese que en ambos ejemplos, se le dio uno de los dos ángulos no rectos. Si ninguno de los dos ángulos no rectos se da, tendrá nueva estrategia para encontrar los ángulos.Usted aprenderá de esta estrategia en el capítulo 4.
Los ángulos de elevación y depresión [ editar ]
Usted puede utilizar triángulos rectángulos para encontrar distancias, si sabes un ángulo de elevación o un ángulo de depresión. La siguiente figura muestra cada uno de estos tipos de ángulos.
El ángulo de elevación es el ángulo entre la línea horizontal de la vista y la línea de visión de hasta a un objeto. Por ejemplo, si usted está de pie en el suelo mirando hacia arriba en la cima de una montaña, se puede medir el ángulo de elevación. El ángulo de la depresión es el ángulo entre la línea horizontal de la vista y la línea de visión hacia abajo a un objeto. Por ejemplo, si estuviera de pie en la cima de una colina o un edificio, mirando a un objeto, se puede medir el ángulo de la depresión. Puede medir estos ángulos usando un clinómetro o un teodolito. La gente tiende a utilizar inclinómetros o teodolitos para medir la altura de los árboles y otros objetos altos. Aquí vamos a resolver varios problemas relacionados con estos ángulos y distancias.
Ejemplo 3
Usted está de pie 20 pies de distancia de un árbol, y se mide el ángulo de elevación a ser de 38 °. ¿Qué altura tiene el árbol?
Solución :
La solución depende de su altura, como se mide el ángulo de elevación de su línea de visión. Suponga que usted es de 5 pies de altura. A continuación, la siguiente figura muestra el triángulo está resolviendo.
La figura nos muestra que una vez que nos encontramos con el valor de T , tenemos que añadir 5 pies a este valor para encontrar la altura total del triángulo. Para encontrarT , debemos utilizar el valor de la tangente:
|
El siguiente ejemplo muestra un ángulo de depresión.
Ejemplo 4
Usted está de pie en la parte superior de un edificio, buscando en el parque en la distancia. El ángulo de la depresión es de 53 °. Si el edificio está de pie sobre es de 100 pies de alto, a qué distancia está el parque? ¿Importa su altura?
Solución :
Si ignoramos la altura de la persona, resolvemos el siguiente triángulo:
Teniendo en cuenta el ángulo de depresión es de 53 °, el ángulo A en la figura anterior es de 37 °. Podemos utilizar la función tangente para encontrar la distancia desde el edificio al parque:
Si tenemos en cuenta la altura si la persona, esto va a cambiar el valor del lado adyacente. Por ejemplo, si la persona es de 5 pies de altura, tenemos un triángulo diferente:
|
Si sólo está buscando para estimar la distancia, de lo que puede pasar por alto la altura de la persona que toma las mediciones. Sin embargo, la altura de la persona se importa más en situaciones donde las distancias o longitudes involucradas son más pequeñas. Por ejemplo, la altura de la persona va a influir en el resultado más en el problema de la altura del árbol que en el problema edificio, como el árbol está más cerca en altura a la persona que el edificio es.
Triángulos rectángulos y Rodamientos [ editar ]
También podemos usar triángulos rectángulos para encontrar distancias utilizando ángulos dados como rodamientos. En navegación, un rodamiento es la dirección de un objeto a otro. En la navegación aérea, se dan los rodamientos como ángulos girar en sentido horario desde el norte. El siguiente gráfico muestra un ángulo de 70 grados:
Es importante tener en cuenta que los ángulos en problemas de navegación se miden esta manera, y no los mismos ángulos forma en que se miden en el círculo unitario.Además, los ángulos en la navegación y la topografía también se pueden dar en términos de norte, este, sur y oeste. Por ejemplo, N 70 ° E se refiere a un ángulo desde el norte, hacia el este, mientras que N 70 ° W se refiere a un ángulo desde el norte, hacia el oeste. N 70 ° E es el mismo que el ángulo que se muestra en el gráfico anteriormente.N ° 70 W resultaría en un ángulo en el segundo cuadrante.
El siguiente ejemplo muestra cómo utilizar un rodamiento para encontrar la distancia.
Ejemplo 5
Un barco viaja en un N 50 ° E supuesto. El barco viaja hasta que se debe al norte de un puerto que está a 10 millas náuticas al este del puerto desde el que se originó la nave. ¿Hasta dónde viajaba la nave?
Solución :
El ángulo opuesto d es el complemento de 50 °, que es 40 °. Por lo tanto podemos encontrar d utilizando la función coseno:
|
Otras aplicaciones de triángulos rectángulos [ editar ]
En general, se puede utilizar la trigonometría para resolver cualquier problema que involucra triángulo rectángulo. Los próximos ejemplos muestran diferentes situaciones en las que un triángulo rectángulo se puede utilizar para encontrar una longitud o distancia.
Ejemplo 6
En la lección 3 presentamos la siguiente situación: usted está construyendo una rampa para que las personas en sillas de ruedas pueden acceder a un edificio. Si la rampa debe tener una altura de 8 pies, y el ángulo de la rampa debe ser de 5 °, ¿cuánto tiempo debe ser la rampa?
Dado que sabemos el ángulo de la rampa y la longitud del lado opuesto al ángulo, podemos utilizar la relación sinusoidal para encontrar la longitud de la rampa, que es la hipotenusa del triángulo:
Esto puede parecer una larga rampa, pero, de hecho, un ángulo de rampa de 5 ° es lo que se requiere por la Ley de Estadounidenses con Discapacidades (ADA). Esto explica por qué muchas rampas están compuesto por varias secciones, o tienen turnos. Se necesita la distancia adicional para compensar la pequeña pendiente.
|
Trigonometría triángulo derecho también se utiliza para la medición de distancias que no pudieron ser medidos realmente. El siguiente ejemplo muestra un cálculo de la distancia entre la luna y el sol. Este cálculo requiere que conocemos la distancia de la Tierra a la Luna. En el capítulo 5 aprenderá la Ley de los senos, una ecuación que es necesaria para el cálculo de la distancia de la Tierra a la Luna. En el siguiente ejemplo, asumimos esta distancia, y el uso de un triángulo rectángulo para encontrar la distancia entre la luna y el sol.
Ejemplo 7
La tierra, la luna y el sol crean un triángulo rectángulo en el primer cuarto de luna. La distancia de la Tierra a la Luna es de unos 240,002.5 millas. ¿Cuál es la distancia entre el Sol y la Luna?
Solución :
Deje d = la distancia entre el Sol y la Luna. Podemos utilizar la función tangente para encontrar el valor de d :
Por lo tanto, la distancia entre el Sol y la Luna es mucho mayor que la distancia entre la Tierra y la Luna.
|
Resumen de la lección [ editar ]
En esta lección hemos vuelto al tema de la trigonometría del triángulo, para resolver problemas del mundo real que involucran triángulos rectángulos. Para encontrar longitudes o distancias, hemos utilizado los ángulos de elevación, ángulos de depresión, ángulos resultantes de rodamientos en la navegación y otras situaciones reales que dan lugar a triángulos rectángulos. En capítulos posteriores, se le extenderá el trabajo de este capítulo usted aprenderá a encontrar ángulos faltantes utilizando relaciones trigonométricas, y usted aprenderá cómo determinar los ángulos y los lados de los triángulos no correctas.
Puntos a considerar [ editar ]
- ¿En qué tipo de situaciones hacen triángulos rectángulos surgen de forma natural?
- ¿Existen triángulos rectángulos que no se pueden resolver?
Trigonometría puede resolver los problemas a escala astronómica, así como los problemas terrenales, incluso a escala molecular o atómica. ¿Por qué es esto cierto?
Preguntas de repaso [ editar ]
- Resolver el triángulo:

- Dos amigos están escribiendo problemas de práctica para estudiar para una prueba de trigonometría. Sam escribe el siguiente problema por su amiga Anna a resolver:
- En la derecha del triángulo ABC , la medida del ángulo C es de 90 grados, y la longitud del lado c es de 8 pulgadas. Resolver el triángulo.
- Anna le dice a Sam que el triángulo no puede ser resuelto. Sam dice que está equivocada. Quien esta bien? Explica tu pensamiento.
- Utilice el Teorema de Pitágoras para verificar los lados del triángulo en el ejemplo 2.
- El ángulo de elevación desde el suelo hasta la parte superior de un asta de bandera se mide a ser 53 °. Si la medida se tomó de 15 pies de distancia, la altura es el asta de la bandera?
- Desde lo alto de una colina, el ángulo de depresión a una casa se mide para ser 14 °. Si la colina es de 30 pies de alto, a qué distancia está la casa?
- Un avión sale de la ciudad A y viaja en un rumbo de 100 °. Ciudad B se encuentra al sur de la ciudad de A . Cuando el avión se encuentra 200 millas al este de la ciudadB , hasta dónde ha viajado por el plan? ¿A qué distancia están la ciudad A y Ciudad B ?

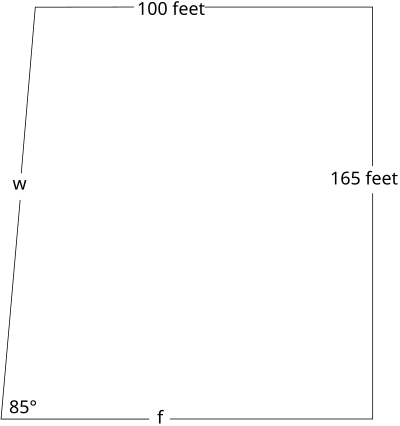
- El moderno edificio se muestra a continuación está construido con una pared exterior (mostrado a la izquierda) que no está en un ángulo de 90 grados con el suelo. La pared de la derecha es perpendicular tanto el suelo y el techo. ¿Cuál es la longitud de la pared exterior inclinada, w ? ¿Cuál es la longitud de la planta principal, f ?
- Un topógrafo es medir el ancho de un estanque. Ella elige un punto de referencia en el lado opuesto de la laguna, y mide el ángulo a este hito desde el punto 50 pies de distancia del punto original. Cuán amplio es el estanque?

- Encuentra la longitud del lado x :

Revisar Respuestas [ editar ]





- Anna es la correcta. No hay suficiente información para resolver el triángulo. Es decir, hay un número infinito de triángulos rectángulos con hipotenusa 8. Por ejemplo:

- 6 2 + 5,03 2 = 36 + 25,3009 61,3009 = 7.83 = 2
- Acerca de 19,9 pies de altura
- Acerca de 120.3 pies
- El avión ha viajado aproximadamente 203 millas. Las dos ciudades están a 35 millas de distancia.
f ≈ 114.44 pies w ≈ 165.63 pies - Acerca de 41,95 pies
- Acerca de 7,44
Vocabulario [ editar ]
- ángulo de depresión
- El ángulo entre la línea horizontal de la vista, y la línea de visión hasta un punto dado.
- ángulo de elevación
- El ángulo entre la línea horizontal de la vista, y la línea de visión hasta un punto dado.
- cojinetes
- La dirección de un objeto a otro, por lo general mide como un ángulo.
- clinómetro
- Un dispositivo usado para medir ángulos de elevación o depresión.
- teodolito
- Un dispositivo usado para medir ángulos de elevación o depresión.
- milla nautica
- Una milla náutica es una unidad de longitud que corresponde aproximadamente a un minuto de latitud a lo largo de cualquier meridiano. Una milla náutica es igual a 1,852 kilometros.

















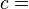



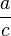







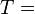
































No hay comentarios:
Publicar un comentario