AMIGOS PARA SIEMPRE: Trigonometría

lunes, 29 de junio de 2015

Trigonometría

Funciones trigonométricas

En trigonometría, el arcoseno está definido como la función inversa del seno de unángulo. Si tenemos:

\arcsin \alpha\,

, su significado geométrico es el arco cuyo seno es alfa.

La función seno no es inyectiva, por lo que no tiene recíproca. Es posible aplicarle una restricción del dominio de modo que se vuelva inyectiva y sobreyectiva. Por convención es preferible restringir el dominio de la función seno al intervalo:

$\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$

Del mismo modo que

y = \sqrt{x}

se puede definir de modo que y² = x, la función y = arcsin(x) se puede definir también de modo que sin(y) = x.

Función arcoseno
Gráfica de Función arcoseno
Definición	$\textstyle f \mbox{ tal que } f(\sin(x))=x \,$
Tipo	Trigonométrica inversa
Dominio	$\textstyle [-1,1]$
Codominio	$\textstyle [-\frac{\pi}{2},\frac{\pi}{2}]$
Imagen	$\textstyle [-\frac{\pi}{2},\frac{\pi}{2}]$
Propiedades	Estrictamente creciente Biyectiva en su dominio
Cálculo infinitesimal
Derivada	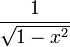$\frac{1}{\sqrt{1-x^2}}$
Función inversa	$\textstyle \sin(x) \quad x \in [-\frac{\pi}{2},\frac{\pi}{2}]$
Funciones relacionadas	arcocoseno arcotangente

El desarrollo en serie de potencias del arcoseno viene dado por:

\sum_{n=0}^{\infty} \frac{(2n)!}{4^n(n!)^2(2n+1)}x^{2n+1}=x+\frac{1}{6}x^3+...

Nótese que este desarrollo solo es válido cuando se expresa el ángulo en radianes. A continuación se da una pequeña demostración de tal desarrollo.

Como función analítica el arcoseno puede extenderse a valores fuera del dominio [-1,1] e incluso complejos. Para valores reales del argumento por encima de +1, la función toma valores complejos:

$\arcsin(1+\varepsilon^2)= \frac{\pi}{2} - i \sum_{k=1}^\infty (-1)^{k+1} a_k \varepsilon^k, \quad a_k > 0, \varepsilon \in \R$

Para valores menores que -1, se tiene en cuenta que:

$\arcsin(-(1+\varepsilon^2))= -\arcsin(1+\varepsilon^2)$

Eso completa la extensión a los números reales, aunque fuera del intervalo [-1,+1] los valores de la función son complejos.En un triángulo rectángulo, el arcoseno equivale a la expresión en radianes del ángulo agudo correspondiente a la razón entre su catetoopuesto y la hipotenusa.

El arcoseno es la función inversa del seno. Es decir:

Al ser el arcoseno y el seno funciones inversas, su composición es la identidad, es decir:

Su abreviatura es arcsen o sen^-1.

Características del arcoseno

Dominio (x):
Codominio (α):
Para poder definir la función inversa de una función, necesariamente debe ser biyectiva. La función seno no es inyectiva en el conjunto de los reales. Por convención, se restringe el codominio al intervalo [-π/2,π/2] para que la función seno sea biyectiva.
La función es continua y creciente en todo el dominio.
Derivada de la función arcoseno:
Integral de la función arcoseno:

Arcoseno de valores característicos

El arcoseno de los valores más característicos es:

Tabla del arcoseno de los valores más característicos (-1,-raiz(2)/2,-1/2,0,1/2,raiz(2)/2,1).

Representación gráfica de la función arcoseno

La gráfica de la función arcoseno es simétrica a la de la función seno respecto a la recta bisectriz del primer y tercer cuadrante (y=x). Con la restricción al intervalo (-π/2, π/2) ambas funciones son crecientes y una inversa de la otra.

Gráfica de las funciones del seno y arcoseno, siendo simétricas respecto la recta y=x.

Se llama arcoseno (arcsen) de un número al ángulo que tiene por seno dicho número. Si se conoce el valor del seno de un ángulo y se quiere calcular el ángulo, hay que tener en cuenta que, salvo en los casos de:

arcsen1=90º y arcsen(-1)=270º,

para cualquier otro número comprendido entre -1 y 1, hay dos ángulos que tienen ese seno.

La fórmula sen(180º-α) = sen(α) indica que si α es uno de los ángulos, el otro será 180º-α.

En el caso particular de arcsen1, un ángulo sería 90º y el otro 180º-90º = 90º. Coinciden los dos.

En el caso particular de arcsen(-1), un ángulo sería 270º y el otro 180º-270º = -90º = 270º. Coinciden los dos.