Funciones circulares de los números reales
y = sin ( x ), El Sine Gráfico [ editar ]
Por ahora, se han convertido en muy familiarizado con los valores específicos de seno, coseno y tangente para determinados ángulos de rotación alrededor de la cuadrícula de coordenadas. En matemáticas, a menudo podemos aprender mucho observando cómo una cantidad cambia cuando variamos sistemáticamente otra. En este caso, ¿qué va a pasar con el valor de, digamos, el seno del ángulo que rotamos gradualmente alrededor de la cuadrícula de coordenadas. Estaríamos viendo el valor de seno como una función del ángulo de rotación alrededor de la cuadrícula de coordenadas. Nos referimos a cualquier función como una función circular, ya que pueden ser definidos usando el círculo unitario. En primer lugar, se recordará a partir de secciones anteriores que el seno de un ángulo en posición estándar en la cuadrícula de coordenadas es la relación entre  , donde y es el y coordenada de cualquier punto en el ángulo y r es la distancia desde el origen hasta ese punto.
, donde y es el y coordenada de cualquier punto en el ángulo y r es la distancia desde el origen hasta ese punto.
 , donde y es el y coordenada de cualquier punto en el ángulo y r es la distancia desde el origen hasta ese punto.
, donde y es el y coordenada de cualquier punto en el ángulo y r es la distancia desde el origen hasta ese punto.
Debido a que las relaciones son las mismas para un ángulo dado, independientemente de la longitud del radio r , podemos usar el círculo unitario para hacer las cosas un poco más cómodo.
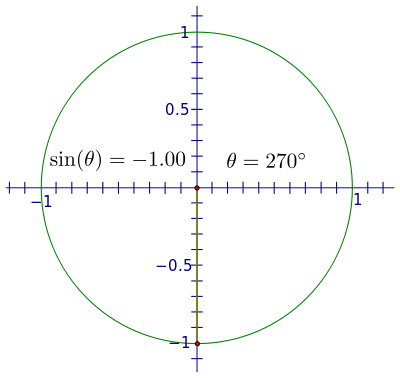
El denominador es ahora 1, así que tenemos el pecado más simple expresión ( θ ) = y . La ventaja de esto es que podemos usar el y coordenada del punto en el círculo unitario para rastrear el valor de sen ( θ ) a través de una rotación completa. Imagínese si empezamos a 0 y luego giramos hacia la izquierda a través de ángulos gradualmente crecientes. Dado que el y coordenada es el valor del seno, ver la altura del punto a medida que gira.
A través de cuadrante I que la altura se hace más grande, a partir de 0, lo que aumenta rápidamente al principio, luego más lento hasta que el ángulo llega a 90 °, y en ese momento, la altura está en su valor máximo, 1.
A medida que gira en el tercer cuadrante, el cambio en la altura ahora se invierte y comienza a disminuir hacia 0.
Cuando usted comienza a girar en el tercer y cuarto cuadrantes, la longitud de los aumentos del segmento, pero esta vez en una dirección negativa, con un crecimiento de -1 a 270 ° y el rumbo de nuevo hacia 0 a 360 °.
Después de una rotación completa, a pesar de que el ángulo continúa aumentando, los valores de seno simplemente repetir sí mismos. Lo mismo habría sido cierto si se optó por girar en sentido horario para investigar los ángulos negativos, y esto explica por qué la función seno es periódica. El período es 2π radianes o 360 °, porque esa es la medida del ángulo requerido antes de que el seno del ángulo de simplemente repetir la secuencia anterior de valores.
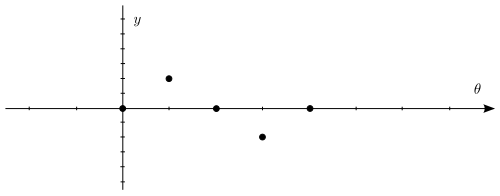
Vamos a traducir este movimiento circular en un gráfico del valor de seno contra el ángulo de rotación. La siguiente secuencia de imágenes demuestra la conexión. Como el ángulo de rotación aumenta, ver el y coordenada del punto en el ángulo que traza horizontal. No haga caso de los valores a lo largo del eje horizontal en este punto, ya que sólo relativa. Lo que es importante es que usted haga la conexión entre la rotación circular y el cambio en la altura del punto.
Observe que una vez que giramos alrededor de una vez, el punto se remonta en los mismos valores de nuevo. La curva roja que se ve es un período de una "ola" sine. La animación muestra que esto suceda en "tiempo real".
Echemos un vistazo a algunos valores concretos para que podamos representar gráficamente la función seno con mayor precisión. Dado que ya sabemos lo que pasa en el medio, se puede dibujar un boceto bastante exacta trazando los puntos para los ángulos de cuadrante (0,  , π,
, π, 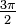 , 2π).
, 2π).
 , π,
, π, 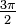 , 2π).
, 2π).
El valor del pecado ( θ ) va de 0 a 1 a 0 a -1 y de nuevo a 0. graficados largo de un eje horizontal que muestra θ , se vería así:
Llenar los vacíos en el medio y que permite múltiples rotaciones, así como los resultados de ángulos negativos en la gráfica de y = sen ( x ), donde x es cualquier ángulo de giro (normalmente expresado en radianes):
Como ya hemos mencionado, el pecado ( x ) tiene un período de 2π. También debe tener en cuenta que los Y -valores nunca pasan por encima de 1 o por debajo de -1, por lo que el rango de una onda sinusoidal es {-1 ≤ y ≤ 1}. Porque podemos seguir girando alrededor del círculo para siempre, no hay ninguna restricción en el ángulo x , por lo que eldominio del pecado ( x ) es todos los números reales.
Y = cos ( x ), el coseno Gráfico [ editar ]
En el capítulo 1 , aprendiste que seno y el coseno están muy estrechamente relacionados. El coseno de un ángulo es el mismo que el seno del ángulo complementario. Por lo tanto, no debe sorprender que las ondas de seno y coseno son muy similares en que ambas son periódica con un período de 2π, un rango de -1 a 1, y un dominio de todos los ángulos reales.
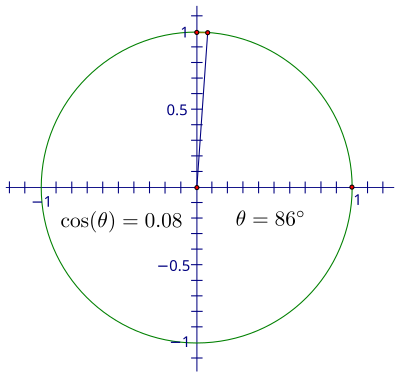
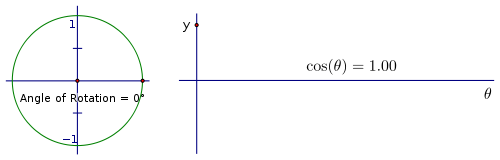
El coseno de un ángulo es la relación de  , por lo que en el círculo unidad, el coseno es la x coordenada del punto de rotación. Si rastreamos la coordenada x través de una rotación, te darás cuenta de que el cambio en la distancia es similar al pecado (x), pero cos ( x ) comienza en un lugar diferente. La coordenada x de un ángulo de 0 ° es 1 y la xcoordenada de 90 ° es 0, por lo que el valor del coseno está disminuyendo de 1 a 0 a través de la 1 st cuadrante.
, por lo que en el círculo unidad, el coseno es la x coordenada del punto de rotación. Si rastreamos la coordenada x través de una rotación, te darás cuenta de que el cambio en la distancia es similar al pecado (x), pero cos ( x ) comienza en un lugar diferente. La coordenada x de un ángulo de 0 ° es 1 y la xcoordenada de 90 ° es 0, por lo que el valor del coseno está disminuyendo de 1 a 0 a través de la 1 st cuadrante.
 , por lo que en el círculo unidad, el coseno es la x coordenada del punto de rotación. Si rastreamos la coordenada x través de una rotación, te darás cuenta de que el cambio en la distancia es similar al pecado (x), pero cos ( x ) comienza en un lugar diferente. La coordenada x de un ángulo de 0 ° es 1 y la xcoordenada de 90 ° es 0, por lo que el valor del coseno está disminuyendo de 1 a 0 a través de la 1 st cuadrante.
, por lo que en el círculo unidad, el coseno es la x coordenada del punto de rotación. Si rastreamos la coordenada x través de una rotación, te darás cuenta de que el cambio en la distancia es similar al pecado (x), pero cos ( x ) comienza en un lugar diferente. La coordenada x de un ángulo de 0 ° es 1 y la xcoordenada de 90 ° es 0, por lo que el valor del coseno está disminuyendo de 1 a 0 a través de la 1 st cuadrante.
Aquí es una secuencia similar de rotaciones a la que utilizamos para el seno. Esta vez comparar los x coordenadas del punto de giro con la altura del punto, ya que traza a lo largo de la horizontal.
La gráfica de y = cos ( x ) tiene un período de 2π. Al igual que el pecado ( x ), el x -valores nunca se "escapan" de la unidad de círculo, para que se mantengan entre -1 y 1. Elrango de una onda coseno es también {-1 ≤ y ≤ 1}. Y también al igual que la función seno, no hay ninguna restricción en el ángulo de rotación, por lo que el dominio de cos ( x) es todos los números reales.
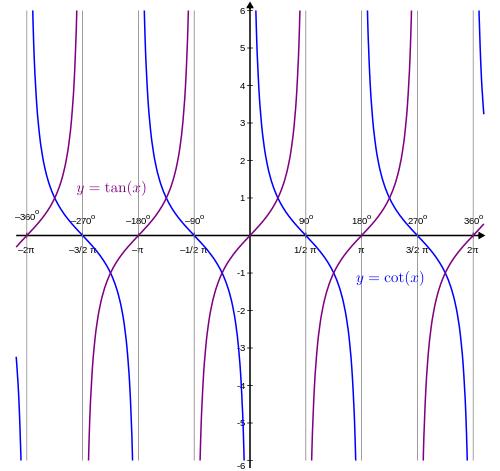
y = tan ( x ), la tangente Gráfico [ editar ]
El gráfico de la relación de tangente como una función del ángulo de rotación presenta algunas complicaciones. Primero de todo, el dominio es ya no todos los ángulos reales.Como es posible que recuerde que hay algunos ángulos (90 ° y 270 °, por ejemplo) para que no se define la tangente. Como veremos en este apartado, el rango de tan ( x ) es en realidad todos los números reales.
La medición de cada una de las seis funciones trigonométricas se puede encontrar mediante el uso de un solo segmento de la unidad de círculo, sin embargo, las funciones restantes no son tan evidentes como seno y coseno. El nombre de la función tangente viene de la línea tangente, que es una línea que es perpendicular al radio de un círculo en un punto en el círculo de modo que la línea toca el círculo exactamente a uno, y sólo uno, punto. Por lo tanto, para crear el segmento tangente, primero trazamos una línea perpendicular a la tangente x eje.
Si extendemos ángulo θ a través de la unidad de círculo de manera que se cruza con la línea de tangente, la función tangente se define como la longitud del segmento rojo.
El segmento de trazos es 1, ya que es el radio de la circunferencia unidad. Recordemos que la tangente de θ es 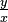 , para que podamos verificar que este segmento es de hecho la tangente usando triángulos semejantes.
, para que podamos verificar que este segmento es de hecho la tangente usando triángulos semejantes.
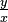 , para que podamos verificar que este segmento es de hecho la tangente usando triángulos semejantes.
, para que podamos verificar que este segmento es de hecho la tangente usando triángulos semejantes.
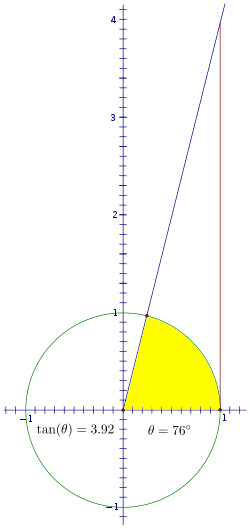
Así, a medida que aumentamos el ángulo de rotación, piense en cómo este segmento cambios. Cuando el ángulo es 0, el segmento no tiene longitud. Al comenzar a girar por el primer cuadrante, aumentará, muy lentamente al principio.
Pero, se puede ver muy pronto que el valor aumenta un pasado. A medida que el ángulo se acerca a 90 °, el segmento tendrá que estirar bastante alto con el fin de interceptar la extensión del ángulo y que crecerá a un ritmo cada vez más rápido.
A medida que muy cerca de la y eje que el segmento se pone infinitamente grande, hasta cuando el ángulo realmente golpea 90 °, en cuyo punto la extensión del ángulo y la recta tangente en realidad ser paralelas y por lo tanto nunca se encuentran!
Esto significa que no hay una definición de la longitud del segmento tangente, o como puede ser útil pensar en ello, el segmento tangente es infinitamente grande .
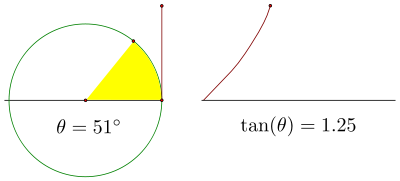
Antes de continuar, vamos a echar un vistazo a esta parte de la gráfica a través del primer cuadrante. La tangente comienza en 0, para un ángulo de 0 °, luego aumenta lentamente al principio. Ese aumento se hace mucho más pronunciada y cuando nos acercamos a una rotación de 90 °.
Una vez más, sólo una pequeña rotura en el x eje sobre estos gráficos hará que sea más claro que estos dos conceptos a tener en cuenta de lado a lado se encuentran en la misma cuadrícula de coordenadas.
De hecho en cuanto tengamos infinitamente cerca de 90 °, el valor de la tangente aumenta sin límite, hasta cuando en realidad llegar a 90 °, en cuyo punto la tangente no está definida. Una línea que una gráfica se pone infinitamente cerca sin tocar se llama una asíntota. Así la función tangente tiene una asíntota en 90 °.
Como rotamos pasado 90 °, ahora la intersección de la prolongación del ángulo y la recta tangente es en realidad por debajo de la x del eje. Esto encaja muy bien con lo que sabemos sobre la tangente para un 2 nd ángulo cuadrante ser negativo. Será primero ser muy, muy negativo, pero como el ángulo de rotación, el segmento se acorta, llega a 0, luego cruza de nuevo en los números positivos como el ángulo entre en el 3 er cuadrante.
El segmento volverá a obtener infinitamente grande, ya que se acerca a 270 °. Después de ser indefinido a 270 °, el ángulo se cruza en el 4 º cuadrante y una vez más cambia de ser infinitamente negativa, al acercarse a cero a medida que completamos una rotación completa.
Por lo tanto, esta moción graficada sobre varias rotaciones se vería así:
Observe que la x eje se mide en radianes (no en términos de π). Nuestros asíntotas ocurren cada π radianes, a partir de  . Por consiguiente, el período de la gráfica es π radianes. El dominio es todos los reales excepto por los "agujeros" en
. Por consiguiente, el período de la gráfica es π radianes. El dominio es todos los reales excepto por los "agujeros" en  ,
, 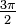 , -
, -  , etc., y el rango es de todos los números reales.
, etc., y el rango es de todos los números reales.
 . Por consiguiente, el período de la gráfica es π radianes. El dominio es todos los reales excepto por los "agujeros" en
. Por consiguiente, el período de la gráfica es π radianes. El dominio es todos los reales excepto por los "agujeros" en  ,
, 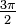 , -
, -  , etc., y el rango es de todos los números reales.
, etc., y el rango es de todos los números reales.Las tres funciones recíprocas: cuna ( x ), csc ( x ) y s ( x ) [ editar ]
Cotangente [ editar ]
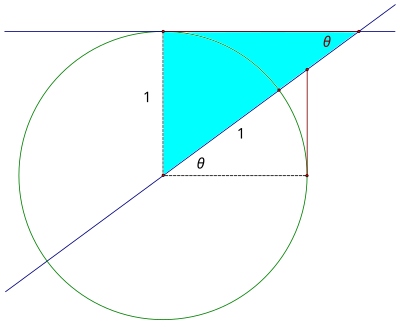
Cotangente es la inversa de la tangente, así que tiene sentido para generar la función circular para cotangente dibujando la línea tangente en un punto de la y el eje y que se extiende el ángulo, en vez de la x del eje.
Podemos verificar que este es el caso de nuevo utilizando triángulos semejantes. Debido a que el segmento cotangente supuesta es paralela a la base del triángulo de color amarillo, a continuación, ángulo θ está en la esquina opuesta y los triángulos son de hecho similares, a pesar de que sus posiciones se invierten.
Por lo tanto,
Ahora que hemos establecido el segmento cotangente, piense en cómo este segmento cambia a medida que giran alrededor de la cuadrícula de coordenadas a partir de 0 °. En primer lugar, a 0 ° sí mismo, la cotangente es indefinido debido a que el segmento es paralelo al rayo del ángulo θ . Al comenzar a aumentar el ángulo de giro, el segmento será muy grande y comenzar a conseguir más pequeño a medida que nos acercamos a 90 °, muy rápido al principio, pero luego desaceleración, ya que se acerca a 0 a los 90 ° de longitud.
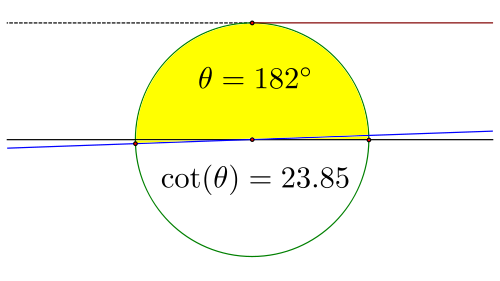
Después de pasar 90 °, el segmento volverá a empezar a alargarse, pero esta vez será en la dirección negativa, aumentando lentamente al principio, luego conseguir infinitamente grande en la dirección negativa hasta 180 °, en cuyo punto es de nuevo indefinido.
Después de pasar por este punto, el comportamiento periódico entra en acción y la función ahora repite la misma secuencia de valores como rotamos de 180 °, de vuelta a 360 °.
Rastreo de esta moción en el gráfico durante varias rotaciones da:
Recuerde que cotangente y la tangente son recíprocos el uno del otro, por lo que cualquier punto en el que la tangente es igual a 0, la cotangente será indefinido y cualquier punto en el que la tangente era indefinido, la cotangente es igual a 0.
También se podría notar que los gráficos se cruzan constantemente en 1 y -1. Estos son los ángulos que tienen ángulos de 45 ° de referencia, que siempre tienen tangentes y cotangentes iguales a 1 o -1. Tiene sentido que 1 y -1 son los únicos valores por los cuales una función y su recíproco son los mismos. Tenga esto en cuenta si nos fijamos en cosecante y secante en comparación con sus recíprocos de seno y el coseno.
La función cotangente tiene un dominio de todos los ángulos reales excepto múltiplos de π {... - 2π. - Π.0, π, 2π ...} El rango es de todos los números reales.
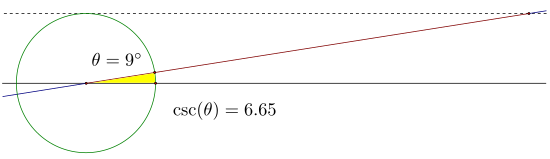
Cosecante [ editar ]
Hay muchas maneras posibles para encontrar el segmento de cosecante. Un enfoque consiste en mirar el triángulo rectángulo formado por el segmento cotangente y utilizar el teorema de Pitágoras para generar la cosecante.
Desde el triángulo original en la unidad de círculo, y 2 + x 2 = r 2
Dado que  es cosecant, entonces el cosecant debe ser el mismo que el lado c .
es cosecant, entonces el cosecant debe ser el mismo que el lado c .
 es cosecant, entonces el cosecant debe ser el mismo que el lado c .
es cosecant, entonces el cosecant debe ser el mismo que el lado c .
Determinación de la longitud de este segmento, que está definido en 0 °, infinitamente grande para ángulos muy pequeños, disminuyendo a 1 en 90 ° y luego aumentando infinitamente hasta que está definido en 180 °. El proceso se repite desde 180 ° a 360 °, sin embargo, el segmento comienza infinitamente negativo, aumenta a -1 a 270 ° antes de acercarse a una longitud infinitamente negativo.
Por consiguiente, el período de la función es 2π con un dominio de todos los ángulos reales excepto múltiplos de π {... -2π, -π, 0, π, 2π ...}. El rango es de todos los números reales mayor que 1 o menor que -1.
El gráfico a continuación, se vería de la siguiente manera:
Aquí está la gráfica de y = sen ( x ), así:
Observe de nuevo las relaciones recíprocas a 0 y las asíntotas. Busque también en los puntos de intersección de las gráficas en 1 y -1. Muchos estudiantes se les recuerda de parábolas cuando miran el período medio de la gráfica cosecante. Si bien son similares en que cada uno tiene un mínimo local o máximo y que comienzan y terminan en el mismo sentido las comparaciones terminan ahí y no deben ser referidos como parabólico. La matemática que define los valores, y por lo tanto a dar forma, de la gráfica es completamente diferente de la función cuadrática de una parábola.
Secante [ editar ]
Al igual que la relación entre el seno y el coseno, secante y cosecante comparten muchas similitudes. El segmento utiliza para generar y = sec ( x ) se muestra a continuación:
Se le pedirá para demostrar esto en la sección de ejercicios. Este segmento es 1 unidad de 0 °, entonces crece a través del primer cuadrante, y está definido en 90 °. Es infinitamente negativa encoge hasta -1 a través de la 2 ª cuadrante, antes de alargar de nuevo hacia la negatividad infinita y no está definido en 270 °. Traduciendo este movimiento a una gráfica de y = sec ( x ) nos da:
Comparándolo con el gráfico coseno:
El período es 2π, el rango es el mismo que y = csc ( x ) { y : y ≥ 1 o y ≤ -1}, y el dominio es todos los ángulos reales, excepto múltiplos de  {... -
{... - 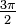 , -
, -  ,
,  ,
, 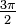 ...}.
...}.
 {... -
{... - 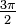 , -
, -  ,
,  ,
, 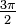 ...}.
...}.Resumen de la lección [ editar ]
Las seis funciones trigonométricas definidas por las relaciones de un triángulo rectángulo se pueden colocar en el contexto de la cuadrícula de coordenadas por pensando en ellos en términos de un punto ( x , y ) que gira alrededor de un círculo centrado en el origen con un radio de uno. Este círculo se llama el círculo unidad . El seno del ángulo de rotación es el y coordenada del punto, el coseno del ángulo es la coordenada x, y la tangente es 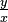 . Los valores de los otros tres relaciones; cotangente, cosecante, secante y también se pueden encontrar en términos de sus relaciones recíprocas, pero todos estos valores se pueden construir geométricamente como diversos segmentos de todo el ángulo de rotación en el círculo unitario. En lugar de encontrar los valores aislados, podemos mirar a cada relación como una función del ángulo de giro. Estos se llamanfunciones circulares . Estos son los dominios y rangos de las seis funciones trigonométricas circulares.
. Los valores de los otros tres relaciones; cotangente, cosecante, secante y también se pueden encontrar en términos de sus relaciones recíprocas, pero todos estos valores se pueden construir geométricamente como diversos segmentos de todo el ángulo de rotación en el círculo unitario. En lugar de encontrar los valores aislados, podemos mirar a cada relación como una función del ángulo de giro. Estos se llamanfunciones circulares . Estos son los dominios y rangos de las seis funciones trigonométricas circulares.
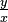 . Los valores de los otros tres relaciones; cotangente, cosecante, secante y también se pueden encontrar en términos de sus relaciones recíprocas, pero todos estos valores se pueden construir geométricamente como diversos segmentos de todo el ángulo de rotación en el círculo unitario. En lugar de encontrar los valores aislados, podemos mirar a cada relación como una función del ángulo de giro. Estos se llamanfunciones circulares . Estos son los dominios y rangos de las seis funciones trigonométricas circulares.
. Los valores de los otros tres relaciones; cotangente, cosecante, secante y también se pueden encontrar en términos de sus relaciones recíprocas, pero todos estos valores se pueden construir geométricamente como diversos segmentos de todo el ángulo de rotación en el círculo unitario. En lugar de encontrar los valores aislados, podemos mirar a cada relación como una función del ángulo de giro. Estos se llamanfunciones circulares . Estos son los dominios y rangos de las seis funciones trigonométricas circulares.Tabla 2.3 Función Dominio Alcance sin ( x ) todos los reales { y : -1 ≤ y ≤ 1} cos ( x ) todos los reales { y : -1 ≤ y ≤ 1} tan ( x ) { x : x ≠ n ·  , donde n es cualquier número entero impar}
, donde n es cualquier número entero impar}todos los reales csc ( x ) { x : x ≠ n π, donde n es cualquier número entero} { y : y > 1 o y <-1 td=""> sec ( x ) { x : x ≠ n ·  , donde n es cualquier número entero impar}
, donde n es cualquier número entero impar}{ y : y > 1 o y <-1 td=""> cuna ( x ) { x : x ≠ n ·  , donde n es cualquier número entero impar}
, donde n es cualquier número entero impar}todos los reales
Preguntas de repaso [ editar ]
- Demostrar que la cara A en este dibujo es igual a seg ( θ ).

- En el capítulo 1, aprendiste ese bronceado 2 ( θ ) + 1 = s 2 ( θ ). Utilice el dibujo y los resultados de la pregunta 1 para demostrar esta identidad.
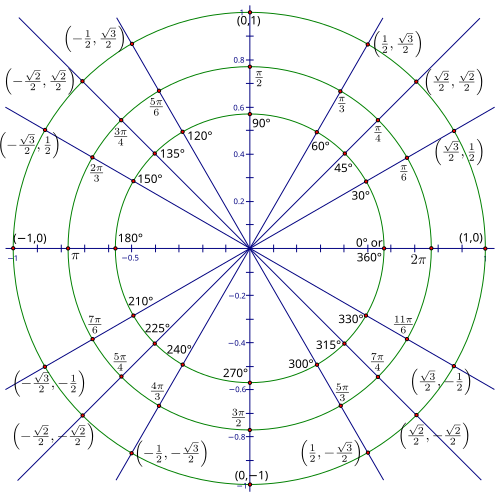
- Este diagrama muestra un círculo unidad con todos los ángulos que tienen ángulos de referencia de 30 °, 45 °, y 60 °, así como los ángulos de cuadrante. Etiquetar las coordenadas de todos los puntos en el círculo unitario. En el círculo más pequeño, etiquetar los ángulos en grados, y en el círculo medio, etiquetar los ángulos en radianes.
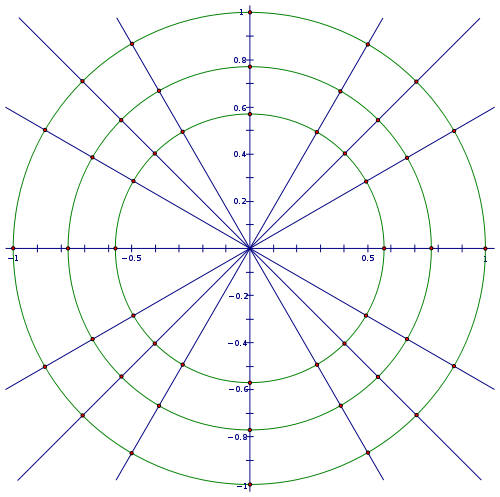
- Dibujar y etiquetar los segmentos de línea en el siguiente dibujo que representan las seis funciones trigonométricas (seno, coseno, tangente, cosecante, secante, cotangente).

- ¿Cuál de los siguientes shows funciones que son a la vez aumentando a medida que x aumenta de 0 a
 ?
?
- (A) sin ( x ) y cos ( x )
- (B) tan ( x ) y csc ( x )
- (C) s ( x ) y cuna ( x )
- (D) csc ( x ) y s ( x )
- ¿Cuál de las siguientes afirmaciones son verdaderas como x aumenta de
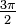 a 2π?
a 2π?
- (A) cos ( x ) se aproxima a 0
- (B) tan ( x ) se pone infinitamente grande
- (C) cos ( x )
x



































































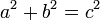
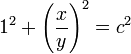

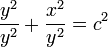





























No hay comentarios:
Publicar un comentario