Funciones trigonométricas
El coseno hiperbólico de un número real 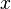 , que se designa mediante
, que se designa mediante  está definido mediante la fórmula:
está definido mediante la fórmula:
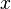 , que se designa mediante
, que se designa mediante  está definido mediante la fórmula:
está definido mediante la fórmula:
Su inversa es el Argumento Coseno Hiperbólico de x, esto se denota por  o bien
o bien 
 o bien
o bien 
- Derivada:
 .
. - Relación con el seno hiperbólico:

- Relación con el coseno:

- Serie de Maclaurin:

- Es una función par:

| Coseno hiperbólico | ||
|---|---|---|
 Gráfica de Coseno hiperbólico | ||
| Definición |  | |
| Tipo | Función real | |
| Dominio |  | |
| Codominio | 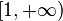 | |
| Imagen | 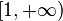 | |
| Propiedades | Biyectiva en el codominio Par Convexa Trascendente | |
| Cálculo infinitesimal | ||
| Derivada |  | |
| Función primitiva |  | |
| Función inversa | 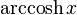 | |
| Límites |   | |
| Funciones relacionadas | Secante hiperbólica Seno hiperbólico Tangente hiperbólica | |
FUNCIONES HIPERBÓLICAS
Las funciones y = sinh x, y = cosh x, y = tanh x.
En forma analítica, estas funciones pueden ser expresadas de forma análoga a las relaciones de Euler para las funciones circulares, esto es:
* gráfica de y = sinh x
| La función senh x crece muy rápidamente hacia infinito , tanto en el eje positivo como en el negativo (hacia infinito negativo). |
* gráfica de y = cosh x
| La función cosh x crece muy rápidamente tanto en el eje positivo como el negativo hacia infinito positivo. |
* gráfica de y = tanh x
| La función y = tanh x tiene por asíntota y=1 en el infinito positivo, y por asíntota y=-1 en el infinito negativo. |
Algunas relaciones:
Las funciones hiperbólicas inversas:
Las funciones inversas de sinh x, cosh x, tanh x, son, respectivamente llamadas "argumento seno hiperbólico", "argumento coseno hiperbólico" y "argumento tangente hiperbólica" (NOTA: algunos autores las llaman "arco seno hiperbólico", "arco coseno hiperbólico" y "arco tangente hiperbólica"):
y = arg sinh x (función inversa de y = sinh x) ,
y = arg cosh x (función inversa de y = cosh x) ,
y = arg tanh x (función inversa de y = tanh x) .
y = arg cosh x (función inversa de y = cosh x) ,
y = arg tanh x (función inversa de y = tanh x) .
De cualquier manera cada una de estas tres funciones tiene otra forma analítica más manejable:
Por ejemplo, para la primera de ellas, podemos partir de:
despejar x:
por lo tanto, la función inversa del seno hiperbólico, y = arg sinh x, puede también ser expresada:
en definitiva, las tres funciones hiperbólicas inversas son:
Cuyas gráficas son:
Observaciones:
* y = arg sinh x se hace + (creciendo muy lentamente) en el infinito positivo, y se hace -
(creciendo muy lentamente) en el infinito positivo, y se hace - , asimismo lentamente, en el infinito negativo.
, asimismo lentamente, en el infinito negativo.
* y = arg cosh x sólo esta definido para valores mayores o iguales a 1, se hace + (creciendo muy lentamente) en el infinito positivo.
(creciendo muy lentamente) en el infinito positivo.
* y = arg tanh x sólo esta definido para valores de x comprendidos entre -1 y +1, se hace + (creciendo rapidisimamente) en x=+1, y se hace -
(creciendo rapidisimamente) en x=+1, y se hace - , asimismo rapidisimamente, en x=-1.
, asimismo rapidisimamente, en x=-1.
Definición analítica
Se llaman funciones hiperbólicas al coseno hiperbólico (denotado cosh o ch), seno hyperbólico (senh o sh) y las funciones que se obtienen a partir de ellas, como la tangente (tanh o th), cotangente (coth), la secante (sech) y la cosecante (cosech) hiperbólicas:
Coseno hiperbólico:
Cotangente hiperbólica:
, definida sobre
y más generalmente sobre
Secante hiperbólica:
Cosecante hiperbólica:
, definida sobre
y más generalmente sobre
.
Sh, th, coth y csch son funciones impares mientras que ch y sech son pares.
Definición geométrica
De la misma manera que las funciones trigonométricas permiten localizarse sobre el círculo trigonométrico, las funciones hiperbólicas dan la posición de un punto cualquiera de la rama positiva de la hipérbola de ecuación
(en un sistema de coordenadas ortonormal).
Un punto A(ch a, sh a) pertenece al esta hipérbola porque sus coordenadas verifican su ecuación, concretamente  .
.
Esto equivale a decir que el sistema  es una representación paramétrica (o ecuación paramétrica) de esta rama de hipérbola.
es una representación paramétrica (o ecuación paramétrica) de esta rama de hipérbola.
Sin embargo lo más sorprendente es que el parámetro a tiene una interpretación geométrica sencilla: es el doble del área delimitada por eje de abscisas, la recta (OA) y la hipérbola (superficie dibujada en azul). La semejanza con la trigonometría circular es llamativa y deja entrever que existe un vínculo muy profundo entre ambas geometrías, la circular (euclídea) y la hiperbólica.
- Prueba: El triángulo OAB tiene como área y el área azulmás él del triángulo OAB mide, integrando para con las ordenadas:.
- El cambio de variable
en la integral anterior da:
. Luego
Relación con la trigonometría
que tiene como consecuencia estas escrituras del coseno y del seno:
- es la parte real de eix, y
- es su parte imaginaria.
Se obtienen fácilmente las relaciones:  ,
,  ,
,  ,
,  .
.
Gracias a estas últimas, se traducen automáticamente todas las relaciones trigonométricas en la lengua de la geometría hiperbólica. Veámos como, con un ejemplo sencillo:
Bien es sabido que
. Es esto cierto para todo x real, luego para todo x complejo (por propiedad de las funciones holomorfas), por tanto para todo complejo de la forma ix:
. Remplazando
por
se obtiene:
es decir
.
En la práctica, una fórmula trigonométrica de cosenos y senos se trasforma en la fórmula similar con
En la práctica, una fórmula trigonométrica de cosenos y senos se trasforma en la fórmula similar con
con sólo cambiar el signo de los eventuales factores
de un término y trasformarlos en
. Por ejemplo
daría
. De aquí en adelante, se escriben en azul los signos que cambian entre la geometría circular y la hiperbólica.
Más generalmente, el factor
Más generalmente, el factor
corresponde a
cuando n = 4k ó n = 4k + 1 , k siendo entero (n es congruente a 0 ó 1 modulo 4) y a
cuando n = 4k + 2 ó n = 4k + 3.
Fórmulas de adición: 
-
- Dividiendo la última fórmula por la penúltima, se obtiene:
- Dividiendo la última fórmula por la penúltima, se obtiene:
Fórmulas de duplicación: se toma y = x en las anteriores. 
Se deducen las fórmulas del medio ángulo: 
Luego, cambinando las fórmulas de adición y de sustracción, se obtienen las de multiplicación, llamadas también de linearización:  que sirven para integrar productos de funciones hiperbólicas.
que sirven para integrar productos de funciones hiperbólicas.
Todo lo anterior permite encontrar las otras fórmulas, sin embargo existe un punto de vista más elegante y teórico que subraya la analogía entre ambas geometrías. Lo exponemos en el párrafo siguiente.
Punto de vista algebraico
Para entender plenamente la trigonometría hiperbólica es preciso realizar el mismo trabajo que se hizo al pasar de los reales a los complejos para entender la trigonometría circular.
Las fórmulas de adición de la geometría circular son consecuencia directa de :
que se escribe
, y que se desarolla en:
Igualando las partes reales (en azul) se obtiene la fórmula del coseno, y con las partes imaginarias (en rojo) la del seno.
Pues bien, remplazando la unidad imaginaria
que verifica
por el número
tal que
sin que
sea 1, ni - 1 ni otro número complejo - se trabaja en el anillo cociente
[1] - se obtienen las fórmulas de adición de ch y sh:
que se desarolla en:
luego en:
(La prueba es similar a la de la fórmula de De Moivre, por inducción sobre n entero natural, luego para n entero negativo).
Como ejemplo se puede calcular
para obtener
y
:
La derivada de ch es sh y recíprocamente, como se puede ver facilmente. Luego, considerando la expresión recién introducida, se observa que:
Esto significa que la función  es solución de la ecuación diferencial
es solución de la ecuación diferencial  y sugiere que, por analogía, f sea denotada con una exponencial:
y sugiere que, por analogía, f sea denotada con una exponencial: 
Esta notación se justifica plenamente al mirar los desarrollos en series de ch x, sh x y  :
:
Sabiendo que  , el desarrollo de
, el desarrollo de  es el siguiente:
es el siguiente:
En resumen:
Esto permite reescribir las dos relaciones anteriores recuadradas así:
Desarrollos en series
Como partes par e impar de la exponencial, los desarollos en series de Taylor del seno y coseno hiperbólicos son los siguientes:
Mediante división euclídea de polinomios se obtienen los desarollos de las demás funciones:
Y en series de Laurent (por el término  ):
):
Funciones recíprocas, derivadas e primitivas
Al restringir adecuadamente sus dominios y codominios, las funciones hiperbólicas se vuelven biyectivas. Su recíprocas tienen una variedad de apelaciones:  según los países y las costumbres. Aquí hemos escogido la notación más corta que prescinde del exponente «-1» que se mezcla mal con el símbolo «'» de la derivación: ash, ach, ath ... (el prefijo "a" es la abreviatura de "área" que proviene de la definición geométrica de estas funciones)
según los países y las costumbres. Aquí hemos escogido la notación más corta que prescinde del exponente «-1» que se mezcla mal con el símbolo «'» de la derivación: ash, ach, ath ... (el prefijo "a" es la abreviatura de "área" que proviene de la definición geométrica de estas funciones)
Estas recíprocas intervienen muy a menudo en el ámbito de las integrales reales, por eso nos hemos restringido al dominio real. sh es biyectiva de  hacia
hacia  , ch lo es delintervalo [0; +∞[ hacia [1; +∞[, th de
, ch lo es delintervalo [0; +∞[ hacia [1; +∞[, th de  hacia ]-1; 1[
hacia ]-1; 1[
- Prueba: Hay que expresar x en función de y en sh x = y:
. Esta ecuación de segundo grado en X tiene como única solución estrictamente positiva
luego, como
(por eso se descarta la solución negativa)
lo que da la expresión de ash.
- Prueba: Obviamente se puede derivar la expresión anterior, pero lo más rápido es utilizar la propiedad de la derivada de la función recíproca:
.
- Las expresiones siguientes se demuestran de la misma manera.
Como consecuencia conocemos la integrales generales siguientes:
Además tenemos, gracias a las demás funciones hiperbólicas recíprocas:
Sin olvidar estas relaciones que no precisan de las recíprocas:  ,
, 
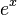

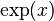 , siendo
, siendo  y exponente
y exponente  .
.
No hay comentarios:
Publicar un comentario