funciones trigonométricas
función cosecante


Los fundamentos de Funciones [ editar ]
Considere dos situaciones que se muestran en los cuadros a continuación:
Situación 1: Su coche puede viajar 30 millas con un galón de gasolina a 55 mph. Por cada milla por hora más rápido que usted conduce, el coche se desplaza a media milla menos por galón de gasolina.
Situación 2: recopilar datos de varios estudiantes en su clase sobre sus edades y sus alturas en pulgadas:
| Edad | 18 | 17 | 18 | 18 | 17 |
| Altura | Sesenta y cinco " | 64 " | 67 " | 68 " | 66 " |
En la primera situación, vamos a la variable x representa la velocidad de su coche, y dejó y representan el número de millas que puede viajar usando un galón de gasolina. Si viaja en x millas por hora, usted irá y = 30-0,5 ( x - 55) millas en un galón de gasolina. Por ejemplo, si se viaja a 60 kilómetros por hora, que viajará 30-0,5 (60-55) = 27,5 millas en un galón de gasolina. Tenga en cuenta que usted puede utilizar su velocidad para "predecir" qué tan lejos puede viajar con un galón de gasolina.
Consideremos ahora la segunda situación. ¿Se puede utilizar los datos a "predecir" la altura, teniendo en cuenta la edad de un estudiante?
Este no es el caso en la segunda situación. Por ejemplo, si un estudiante tiene 18 años, hay varias alturas que el estudiante podría ser.
Ambas situaciones son las relaciones. Una relación es simplemente una relación entre dos conjuntos de números o datos. Por ejemplo, en la segunda situación, hemos creado una relación entre edades y alturas de los estudiantes, con sólo escribir la información de cada estudiante como un par ordenado. En la primera situación, existe una relación entre la velocidad del vehículo y la eficiencia con que se puede utilizar un galón de gasolina. El primer ejemplo es diferente de la segunda porque representa una función : cadax está emparejado con un solo y. Algunas relaciones son matemáticamente importante. Por ejemplo, los círculos y elipses son representaciones gráficas de las relaciones importantes entre x y Y coordenadas, pero no hay una única y coordinar para cada x de coordenadas. Debido a la única y para cada x , funciones desempeñan un papel importante en las matemáticas y la ciencia.
Podemos representar funciones de muchas maneras. Algunas de las formas más comunes para representar funciones incluyen: conjuntos de pares ordenados, ecuaciones y gráficos. La siguiente figura muestra una función representada en cada una de estas representaciones:
Tabla 1.1: Ejemplos de funciones Representación Ejemplo Conjunto de pares ordenados (1,3), (2,6), (3,9), (4,12) (un subconjunto de los pares ordenados para esta función) Ecuación Y = 3 x Gráfico
En contraste, las relaciones que se muestran en la figura de abajo son no funciones:
Tabla 1.2: Ejemplos de funciones no- Representación Ejemplo Conjunto de pares ordenados (4,2), (4, -2), (9,3), (9, -3) (un subconjunto de los pares ordenados para esta función) Ecuación x = y 2 Gráfico
Para comprobar que esta relación no es una función, hay que demostrar que por lo menos un x valor se empareja con más de una y de valor. Si nos fijamos en la primera representación, el conjunto de pares ordenados, se puede ver que el 4 se empareja con 2 y con -2. Del mismo modo, 9 se empareja con 3 y con -3. Por lo tanto la relación no es una función. Si nos fijamos en el gráfico anterior, podemos ver que, excepto para x = 0, los x valores de la relación son cada emparejados con dos Y valores. Por lo tanto la relación anterior no es una función.
Una manera de determinar rápidamente si una relación es una función es realizar la prueba de línea vertical , lo que significa que usted dibuja una línea vertical a través de la gráfica. Por ejemplo, si trazamos la línea x = 4 a través de la gráfica de x = y 2 , la línea se cruzará la gráfica dos veces. Esto significa que la relación no es una función.
Ejemplo 1
Determinar si la relación es una función o no.
a. (2,4), (3,9), (5,11), (5,12)
b.
Solución :
a. Esta relación no es una función porque 5 se empareja con 11 y con 12. Si trazó los puntos, la línea x = 5 tocaría 2 puntos en la relación.
b. Esta relación es una función porque cada x está emparejado con una sola y .
|
Una vez que son capaces de determinar si una relación es una función, a continuación, debe ser capaz de indicar el conjunto de x valores y el conjunto de Y. valores por los que se define una función.
El dominio de una función se define como el conjunto de todos los x valores por los que se define la función. Por ejemplo, el dominio de la función y = 3 x es el conjunto de todos los números reales, a menudo escrito como  . Esto significa que x puede ser cualquier número real. Otras funciones han restringido dominios. Por ejemplo, el dominio de la función
. Esto significa que x puede ser cualquier número real. Otras funciones han restringido dominios. Por ejemplo, el dominio de la función  es el conjunto de todos los números reales mayores o iguales a cero. El dominio de esta función se limita de esta manera debido a que la raíz cuadrada de un número negativo no es un número real. Por lo tanto, el dominio se limita a valores no negativos de x para que se definirán los valores de la función.
es el conjunto de todos los números reales mayores o iguales a cero. El dominio de esta función se limita de esta manera debido a que la raíz cuadrada de un número negativo no es un número real. Por lo tanto, el dominio se limita a valores no negativos de x para que se definirán los valores de la función.
 . Esto significa que x puede ser cualquier número real. Otras funciones han restringido dominios. Por ejemplo, el dominio de la función
. Esto significa que x puede ser cualquier número real. Otras funciones han restringido dominios. Por ejemplo, el dominio de la función  es el conjunto de todos los números reales mayores o iguales a cero. El dominio de esta función se limita de esta manera debido a que la raíz cuadrada de un número negativo no es un número real. Por lo tanto, el dominio se limita a valores no negativos de x para que se definirán los valores de la función.
es el conjunto de todos los números reales mayores o iguales a cero. El dominio de esta función se limita de esta manera debido a que la raíz cuadrada de un número negativo no es un número real. Por lo tanto, el dominio se limita a valores no negativos de x para que se definirán los valores de la función.
A menudo es fácil determinar el dominio de una función de (1) teniendo en cuenta lo que podría haber restricciones y (2) mirando un gráfico.
Ejemplo 2
Indique el dominio de cada función.
a. y = x 2
b.

c. (2, 4), (3, 9), (5, 11)
Solución :
a. El dominio de esta función es el conjunto de todos los números reales. No hay restricciones.
b. El dominio de esta función es el conjunto de todos los números reales, excepto x ≠ 0. El dominio se restringe de esta manera porque una fracción con denominador cero no está definido.
c. El dominio de esta función es el conjunto de x valores {2, 3, 5}.
|
La variable x se refiere a menudo como la variable independiente, mientras que la variable y se conoce como el dependiente variable. Hablamos de x y de y de esta manera porque los Y valores de una función depende de lo que las x son los valores. Por eso también decimos que " y es una función de x ". Por ejemplo, el valor de y en la función y = 3 x depende de lo que x valor que estamos considerando. Si x = 4, podemos determinar fácilmente que y = 3 (4) = 12.
Cuando estamos trabajando con una función en la forma de una ecuación, hay una notación especial que podemos utilizar para enfatizar el hecho de que y es una función de x .Por ejemplo, la ecuación Y = 3 x también pueden escribirse como f ( x ) = 3 x . Es importante recordar que f ( x ) representa los Y valores o los valores de la función, y que la letra f es no una variable. Es decir, f ( x ) no , no queremos decir que estamos multiplicando un número f por otro número x . Piense de una función como una máquina que toma en un número, x , y produce otro número. En la expresión f ( x ), f es la máquina y el paréntesis () son el lugar donde la entrada, x , se introduce en la máquina. f ( x ) es la salida que la máquina produce con la entrada x . Por ejemplo, considere la posibilidad de que su máquina añade 5 a una entrada. Entonces f (3) = 8, o más generalmente, f ( x ) = x + 5.
Ahora que hemos considerado el dominio de una función, giraremos a la gama de una función, que es el conjunto de todos Y valores por los que se define una función. Al igual que hicimos con el dominio, podemos examinar una función y determinar su alcance. Una vez más, a menudo es útil para pensar en lo que podría haber restricciones, y lo que la gráfica de la función se parece. Considere, por ejemplo, la función y = x 2 . El dominio de esta función es todos los números reales, pero ¿qué pasa con el rango?
El rango de la función es el conjunto de todos los números reales mayores o iguales a cero. Este es el caso, porque cada y valor es el cuadrado de un x valor. Si elevamos al cuadrado los números positivos y negativos, el resultado siempre será positivo. Si x = 0, y = 0. También podemos ver la gama, si nos fijamos en un gráfico de y = x 2 :
Algunas funciones tienen saltos repentinos. Considere la función de "redondeo" que toma un número y redondea al número entero más próximo (redondeando hacia arriba si el número es exactamente entre dos números enteros). Así algunos valores para esta función son (2, 2), (1,4, 1), (3,9, 4), (5,5, 6), y (-5,5, -5). El dominio de esta función es todos los números reales, pero el rango de la función es los números enteros.
Otra función que salta proviene de la forma a menudo cobran los taxis. Supongamos que un taxi cuesta $ 5.00 para los primeros 2 millas, pero entonces $ 1 por cada milla adicional o fracción de milla. Considere la función que tiene la distancia recorrida como la entrada y el costo de la taxi como la salida. Así algunos valores para esta función son (1, 5), (1,9, 5), (2,1, 6), (10, 13). El dominio de esta función es que los números reales no negativos (ya que no puede recorrer una distancia negativa en un taxi). La gama de esta función es todos los números enteros positivos mayores que o igual a 5: {5, 6, 7, 8, ...}.
Ejemplo 3
Indique el dominio y el rango de la función

Solución :
Para esta función, podemos elegir cualquier x valor, excepto x ≠ 0. Por tanto, el dominio de la función es el conjunto de todos los números reales, excepto x ≠ 0.
La gama también está restringida a los números reales distintos de cero, pero por una razón diferente. Debido a que el numerador de la fracción es 2, el numerador nunca puede ser igual a cero, por lo que la fracción puede cero nunca es igual.
|
Ahora que hemos definido lo que significa para una relación con una función, y hemos definido dominio y el rango de una función, podemos ver algunos ejemplos específicos de funciones y sus gráficas.
Familias de Funciones [ editar ]
Los ejemplos que hemos visto hasta ahora han incluido varios tipos diferentes de funciones. A partir de su experiencia previa trabajando con ecuaciones y gráficos, es posible que ya haya realizado las conexiones entre las formas de las ecuaciones de funciones y lo que los gráficos parecen. Aquí vamos a examinar varias "familias" de funciones. Una familia de funciones es un conjunto de funciones cuyas ecuaciones tienen una forma similar. El "padre" de la familia es la ecuación en la familia con la forma más simple. Por ejemplo, y = x 2 es un padre para otras funciones, como por ejemplo y = 2 x 2 - 5 x + 3. El siguiente cuadro resume los aspectos clave de varias familias de funciones.
Todas estas funciones se pueden utilizar para representar situaciones reales. Por ejemplo, la función lineal y = 3 x se utilizó anteriormente para representar la cantidad de dinero que haría la venta de barras de chocolate por $ 3.00 cada uno. Este tipo de situación se conoce como variación directa . Decimos que la cantidad de dinero que gana varía directamente con el número de barras de caramelo que usted vende. Variación directa entre dos variables siempre se modela con una función lineal de la forma y = mx . La pendiente de la recta, m , es la constante de variación. Observe que el y interceptación de la línea es 0; es decir, la línea contiene el punto (0, 0). Esto tiene sentido en términos de la situación de venta de dulces: si vendes 0 barras de caramelo, se hace 0 dólares.
Otras situaciones pueden ser modelados con un tipo diferente de la función lineal. Considere la siguiente situación: un restaurante está teniendo un especial: una pizza grande de queso cuesta $ 8,00, y cada relleno cuesta $ 2.00. El costo de una pizza puede ser modelada con la función de c ( x ) = 2 x + 8, donde x es el número de coberturas en la pizza. La pendiente de la línea es de 2, ya que cada relleno añade 2 dólares al precio. El y interceptación es 8: si usted no elige cualquier coberturas adicionales, la pizza cuesta $ 8.00.
Funciones polinómicas cuadráticas, cúbicas, y otras se pueden utilizar para modelar muchos tipos de situaciones Otra familia importante de funciones es las funciones racionales, o cocientes de polinomios, tales como:
Por ejemplo, una función racional se utiliza para modelar variación inversa entre dos variables. Variación inversa significa que el producto de dos variables es constante: xy = k. Si resolvemos esta ecuación para y , tenemos  , una función racional. El siguiente ejemplo muestra variación inversa en una situación real:
, una función racional. El siguiente ejemplo muestra variación inversa en una situación real:
 , una función racional. El siguiente ejemplo muestra variación inversa en una situación real:
, una función racional. El siguiente ejemplo muestra variación inversa en una situación real:
Ejemplo 4
Algunos días en coche al trabajo, y otros días que montan su bicicleta. Ayer usted condujo a una velocidad promedio de 40 millas por hora, y se tomó 15 minutos. Hoy usted montó su bicicleta una velocidad de 20 millas por hora, y se tomó media hora.
Escribe una ecuación que muestra la relación entre la velocidad y el tiempo que se tarda en llegar al trabajo.
Solución :
En primer lugar, tenga en cuenta que la distancia entre el hogar y el trabajo es de 10 millas:
Sabemos que, en general:
Por lo tanto si usted conduce un vehículo o paseo a una velocidad de x millas por hora, que le llevará Y horas para llegar al trabajo:
 . . |
En general, las funciones se pueden utilizar para modelar fenómenos reales en muchos contextos, incluyendo las diferentes áreas de la ciencia, los negocios, la economía, y más. El tipo de función que se puede utilizar para modelar una situación específica depende de los aspectos clave de una función que se ajuste a los aspectos clave de la situación. Un aspecto de muchas situaciones no se ve en los tipos de funciones que hemos visto hasta ahora, pero se verá en las funciones trigonométricas que aprenderá en este capítulo. Consideremos, por ejemplo, la siguiente tabla, que muestra las temperaturas medias mensuales altas y bajas en la ciudad de Boston, MA, de 1971 a 2000. (Fuente: rssweather.com)
Tabla 1.4: Las temperaturas medias mensuales altas / bajas para Boston, MA Mes Bajo Alto Enero 22.1 ° F 36.5 ° F Febrero 24.2 ° F 38.7 ° F Marzo 31.5 ° F 46.3 ° F Abril 40.5 ° F 56.1 ° F Mayo 50.2 ° F 66.7 ° F Junio 59.4 ° F 76.6 ° F Julio 65.5 ° F 82.2 ° F Agosto 64.5 ° F 80.1 ° F Septiembre 56.8 ° F 72.5 ° F Octubre 46.4 ° F 61.8 ° F Noviembre 37.9 ° F 51.8 ° F Diciembre 27.8 ° F 41.7 ° F
El siguiente gráfico muestra las bajas temperaturas promedio.
Observe que el gráfico incluye un año completo de datos, y luego termina con diciembre, el 12 º mes. Es posible que la curva sugerido por este gráfico se puede aproximar por una función en una de las familias de funciones que hemos discutido. No todos los fenómenos naturales puede ser modelado con funciones matemáticas, pero muchos pueden.
Supongamos que este dato era representante de Boston tiempo en general. Podríamos hacer una función cuya entrada es el tiempo en meses desde el presente y cuya salida es la temperatura media se esperaba. Por ejemplo f (1) = 22,1, f (5) = 50,2. La función se repetirá después de un año. ¿Qué representan 13? ¿Cuál es la temperatura que se espera en base a estos datos?
Debido a que el ciclo de meses de cada año, el 13 representa de enero del próximo año, y en general, podemos predecir el clima en enero dado nuestro conocimiento del clima habitual en un lugar. Por ejemplo, enero es el mes más frío del año en la ciudad de Boston. Durante los años que se muestran en la tabla, la temperatura baja promedio fue de cerca de 22 grados. Por lo tanto, podemos predecir que la baja temperatura media en enero en Boston será de unos 22 grados. Podríamos utilizar esta función para comparar el tiempo actual al tiempo pasado y prueba de los cambios climáticos en el tiempo.
Debido a que los meses del año y los patrones climáticos son cíclicos en la naturaleza, tenemos que modelar esta situación con una función que también es de naturaleza cíclica. Tales funciones se denominan periódica . Una función es periódica si existe algún valor p tal que f ( x + p ) = f ( x ) para todo x en el dominio de la función. Las funciones trigonométricas que aprenderá en este capítulo son un tipo de función periódica, y podemos usar ciertas funciones trigonométricas para modelar los datos meteorológicos que se muestran arriba. Volveremos a este tema al final de esta lección, pero ahora vamos a ver en las gráficas de funciones.
Funciones gráficas y herramientas tecnológicas [ editar ]
Si bien existen técnicas que puede utilizar para graficar de manera eficiente muchas funciones a mano, utilizando una calculadora gráfica le permite graficar rápidamente cualquier función, y para identificar los aspectos clave de la función. Los dos ejemplos siguientes le mostrarán cómo usar una calculadora gráfica TI para explorar una función.
Ejemplo 5
Representa gráficamente la función y = x 3 - 3 x 2 + 1
a. Evaluar la función para x = 0, x = 2, y x = -2.
b. Describir el comportamiento final de la función.
c. Aproximado todos x -intercepts.
d. Aproximado cualquier máximos y mínimos locales.
Solución :
Para graficar esta función, pulse [Y =] , y borrar cualquier ecuaciones ya introducidos. En Y1 , introduzca la ecuación. Si usted nunca ha entrado en una ecuación antes, he aquí algunos consejos:
Una vez que haya entrado en la ecuación, pulse [ZOOM] [6] . Esto le llevará a la ventana "estándar": se puede ver tanto x e y de -10 a 10. (Tenga en cuenta que si se desplaza hacia abajo a la opción 6, hay que pulsar ingrese Sin embargo, si usted acaba de entrar en el número 6. , se le llevará a la gráfica.)
a. Para evaluar la función, puede "rastrear" en el gráfico. Pulse el [TRACE] botón. Usted debe ver la ecuación en la parte superior de la pantalla, y el cursor debe estar en el yinterceptación, (0, 1). En la parte inferior de la pantalla debería ver x = 0 y y = 1. Este nos dice que para x = 0, el valor de la función es 1.
Ahora que está en el modo de rastreo, puede introducir cualquier x valor y la calculadora le dirá el y valor. Por ejemplo, si pulsa [2] [ENTER] , verá el cursor movimiento hasta el punto (2, -3) y en la parte inferior de la pantalla, verá x = 2 y Y = -3. Si pulsa [(-)] [2] [ENTER] , verá x = -2 y y = -19 en la parte inferior de la pantalla. Observe que no puede ver el punto de la gráfica. Para ver este punto, tenemos que cambiar la ventana. Presione [VENTANA] y desplácese hacia abajo para Ymin. Cambie la -10 a -25. A continuación, pulse [GRÁFICO] . Ahora presione [TRACE] [(-)] [2] [ENTER] . Usted debe ver el punto (-2, -19).
b. Comportamiento de finalización: el lado izquierdo de la gráfica parece estar bajando, y el lado derecho parece estar subiendo. Si queremos ver más de la gráfica, podemos alejar la imagen. Presione [ZOOM] [3] . Esto aumentará el tamaño de la ventana. Si presione [ENTER] de nuevo, la ventana aumentará de nuevo. Si lo hace dos veces, te darás cuenta de que los ejes se ven gruesas y que la gráfica es difícil de ver. Esto es porque las marcas de graduación sobre los ejes se establecen en 1s. Presione[VENTANA] y desplácese hacia abajo para Xscl. Si pulsa [BORRAR] , esto eliminará todas las marcas de graduación. (También puede establecer la escala a algo más grande.). Para ver el gráfico mejor, también puede reducir el Xmin y Xmax. Establecer Xmín a -20ºC y Xmax a 20. Presione [GRÁFICO] . Ahora puede ver la función. Presione[TRACE] en cualquier dirección, y usted será capaz de ver que el lado izquierdo de la gráfica continúa bajando, y el lado derecho sigue subiendo. c. La x -intercepts: regresar el gráfico a una ventana más pequeña, pulse [ZOOM] [6] . Si desea ver el gráfico en una ventana más pequeña, pulse [ZOOM] [4] . Usted debe ver que la gráfica tiene 3 x -intercepts. Usted puede aproximar visualmente trazando: pulse [TRACE] y mover el cursor hacia la izquierda. El extremo izquierdo xinterceptación es de alrededor de -.5. Para encontrar una buena aproximación de la x interceptación, pulse [2nd] [TRACE] [2] . Esto le devuelve a la gráfica. En la pantalla aparecerá la pregunta "izquierda unida?" Mueva el cursor a la izquierda de la x interceptación. (Usted va a mover hacia abajo, en este caso.) Pulse [ENTER] . A continuación podrá ver la pregunta "En este límite?" Mueva el cursor a la derecha de la x interceptación, pero no ir demasiado lejos (Usted no quiere pasar la próxima x interceptación.) Pulse [ENTER] . A continuación, se le pedirá que "adivinar" el intercepto. Mover el cursor hacia la izquierda, tan cerca de la x interceptación posible. Presione [ENTER] . Usted debe ver x = -.5320888. Esta es una aproximación de la x interceptación. Si utiliza los mismos pasos de uso, usted encontrará que los demás x -intercepts son aproximadamente 0,6527 y 2,879. d. Máximos y mínimos: observe que el gráfico como un "cerro" y un "valle". El cerro se llama un "máximo local", ya que es el punto más alto en el gráfico, dentro de un cierto intervalo. El valle es igualmente un "mínimo local". Para aproximar las coordenadas del máximo, pulse [TRACE] y rastrear cerca del máximo. Parece que el máximo es (0, 1).Para comprobar esto, pulse [2nd] [TRACE] [4] . Para encontrar el máximo, tenemos que hacer lo mismo "izquierdo, extremo derecho, supongo" proceso que usamos para encontrar las intersecciones x. Este proceso debería decirle que el máximo es (0, 1). (Nota: el x valor puede decir algo como "9.64487 E Esto es sólo un pequeño error calculadora Este número está muy cerca de 0 -7. ".!) Para encontrar el mínimo rastro hacia el" valle ". (Si lo desea, puede ir a la [VENTANA] y hacer que el Ymín un número más bajo, por lo que se puede ver claramente el mínimo de la gráfica.) Ahora pulse [2nd] [TRACE] [3] . Esto le llevará de vuelta a la gráfica. Hacer el proceso de "izquierda, extremo derecho, adivinar" que debe mostrar que el punto mínimo es (2, -3). |
Ejemplo 6
Usted tiene 100 pies de la cerca con la que encierran una parcela de tierra en el lado de un granero. ¿Quieres la tierra adjunta a ser un rectángulo.
a. Escriba una función para modelar la superficie de la parcela en función de la anchura de la parcela.
b. Representa gráficamente la función usando una calculadora gráfica.
c. ¿Qué tamaño rectángulo debe usted hacer con la valla con el fin de maximizar el área del recinto rectangular?
d. Explicar el significado de los x -intercepts.
Solución :
El terreno se verá como la imagen de abajo:
a. La ecuación: El área de la trama rectangular es el producto de su longitud y anchura. Podemos escribir el área como una función de x : A ( x ) = 2 xh . Podemos eliminar hde la ecuación, si tenemos en cuenta que contamos con 100 pies de la cerca, y escribir una ecuación acerca de cómo estamos utilizando que 100 pies de la cerca: x + 2 h = 100. (El cuarto lado del rectángulo no lo hace requerir la cerca por el granero) Podemos resolver esta ecuación para. h y sustituir en la ecuación zona: b. El gráfico: Pulse [Y =] y borrar cualquier ecuaciones. A continuación, introduzca la ecuación en Y1 . Observe que si pulsa [ZOOM] [6] , no verá ningún gráfico. Usted puede alejar pulsando [ZOOM] [3] , pero puede ser más eficiente para elegir una ventana basada en los valores de función. Pulse [2nd] [VENTANA] con el fin de configurar la tabla. TblStart es la primera entrada que desea ver en la tabla. Tbl le permite establecer los incrementos. Por ejemplo, si usted quiere ver x = 1, 2, 3, 4, etc., ajuste esta a 1. Para este ejemplo, establezca este a 10. Asegúrese Indpnt y Depend ( x y y ) se ajusta en "auto" . A continuación, pulse [2nd] [GRÁFICO] para ver la tabla. Si se desplaza a través de la mesa, se verá que el y valor alcanza 2500 en x = 50, y luego los valores disminuir. Ahora podemos configurar la ventana. Presione [VENTANA] . y establecer Xmin = -1, Xmax = 105, Ymin = -200 y Ymax = 3000. (Nota: puede establecer Xmin y Ymín cada uno a 0, pero poniéndolos en -1 y -200 le permite ver los ejes. )
La gráfica de A ( x ) se muestra aquí en el intervalo [0, 100].
c. La superficie máxima posible: mediante el proceso del ejemplo 6, se debe constatar que (50, 2500) es el punto máximo. Esto nos dice que cuando el ancho del rectángulo es de 50 pies, el área es 2.500 pies 2 . d. Intercepta: Usando el proceso del ejemplo 5, usted debe encontrar que las x intercepta están a 0 y 100. Esto nos dice que si el ancho del jardín es 0, entonces el área es 0. Si el ancho de la parcela de tierra es 100, entonces el área es 0. Este es el caso porque hay sólo 100 pies de la cerca. Si la anchura es 100, no hay más cerca para el resto del rectángulo! |
Introducción a las funciones trigonométricas [ editar ]
Consideremos de nuevo los datos de temperatura de arriba:
Como se ha indicado anteriormente, este tipo de datos necesita ser modelada con una función que es periódica. En particular, este tipo de datos es a menudo modelada por una sinusoide, un gráfico que oscila de una manera particular, como se ve en el gráfico siguiente.
Cada sinusoide repite sus valores en un intervalo regular. Si modelamos la información del tiempo con un gráfico de este tipo, los valores se repetirán cada 12 meses. Por eso decimos que el período de la función es 12.
Observe que los datos varía de aproximadamente 22 a 65. Observe también que la "ola" en los centros de entre estos valores, en torno a y = 43. Por lo tanto, decir que la amplitud de la onda es de aproximadamente 21, que es la distancia desde el centro de la parte superior o la parte inferior de la onda.
Muchos fenómenos reales puede ser modelado con este tipo de función.
Resumen de la lección [ editar ]
En esta lección hemos revisado el concepto de una función, incluidos los principales aspectos de las funciones, y diferentes tipos de funciones. También hemos utilizado calculadoras gráficas para graficar y explorar funciones diferentes. Un punto clave de esta lección es que podemos usar funciones para modelar fenómenos reales. Un segundo punto clave es que con el fin de modelar fenómenos que son de naturaleza cíclica, tenemos que utilizar funciones que son periódicas. En la lección 4 en este capítulo vamos a definir seis funciones trigonométricas. Sin embargo, debido a que las entradas de estas funciones son ángulos, en los próximos dos lecciones nos centraremos en los ángulos.En primer lugar vamos a revisar los ángulos en los triángulos de la geometría, y luego consideraremos ángulos en rotación.
Puntos a considerar [ editar ]
- Lo que distingue a una función de una relación?
- ¿Qué hace que una función periódica?
- ¿Cuáles son los pros y los contras del uso de una calculadora para graficar una función?
Preguntas de repaso [ editar ]
- Determinar si cada relación es una función:
- Un tren viaja a una velocidad constante de 95 millas por hora.
- (A) Escriba una ecuación que muestra la relación entre el número de horas que el tren ha viajado y la distancia que ha recorrido.
- (B) ¿Es esta variación situación directa, la variación inversa, o ninguno?
- (C) Use la ecuación para determinar la distancia del tren ha recorrido después de 3 horas.
- Usted decide iniciar un pequeño negocio de fabricación de marcos. Usted gasta $ 100 en la pintura y otros materiales de construcción, así como $ 2.00 por marco de madera. Usted decide vender cada cuadro por $ 10.00.
- (A) Escriba una función lineal que los modelos de los costos de su negocio.
- (B) Escriba una función lineal que modela el ingreso de su negocio. (Ingresos es la cantidad de dinero que usted toma pulg.)
- (C) Escriba una función lineal que los modelos de las ganancias de su negocio. (Los beneficios se pueden encontrar restando los gastos de los ingresos.)
- (D) Utilice su función de utilidad para determinar el número mínimo de cuadros que deben ser vendidos para obtener un beneficio.
- Considere la función definida por la ecuación f ( x ) = x 2 - x - 3.
- (A) ¿A qué familia pertenece esta función?
- (B) Estado del dominio y el rango de la función.
- (C) Use una calculadora gráfica para graficar la función, para identificar las coordenadas aproximadas del vértice, y los valores aproximados de la x -intercepts.
- Considere la función
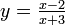
- (A) Utilice una calculadora gráfica para graficar la función.
- (B) Identificar todas las asíntotas.
- El precio de la reserva de un salón de fiestas privadas en un restaurante es de $ 500. El precio por persona es inversamente proporcional a la cantidad de personas que asisten a la fiesta.
- (A) Escriba una ecuación que representa la relación entre c, el costo por persona, yp el número de personas que asisten.
- (B) Utilice la ecuación para encontrar el costo por persona si 32 personas asisten.
- Utilice una calculadora gráfica para graficar las funciones Y = x 3 + x , Y = x 3 + 2 x , y = x 3 - x , y Y = x 3 - 2 x . ¿Cuál es el efecto de cambiar el coeficiente del segundo mandato?
- La ecuación p ( x ) = -.5 x 2 + 90 x - 200 representa las ganancias de una empresa, donde x es el número de unidades de la empresa comercializa. Utilice una calculadora gráfica para graficar la función, y el uso de la gráfica para contestar las preguntas.
- (A) ¿Cuál es el beneficio máximo, y cuántas unidades debe vender para alcanzar el máximo beneficio?
- (B) Hallar los x -intercepts y explicar el significado de estos puntos en la gráfica, en términos de los beneficios de la empresa.
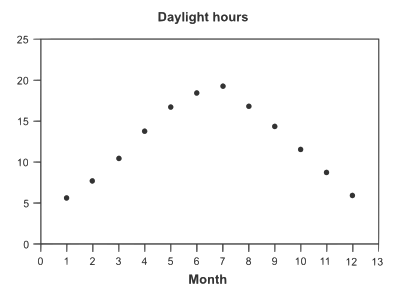
- La siguiente tabla muestra el promedio de horas de luz del día cada mes en Anchorage, Alaska.
- (A) Usa tu calculadora gráfica para representar los datos, o el gráfico con la mano. Utilice enero = 1.
- (B) ¿Cuál es el período de los datos?
- (C) ¿Cómo podría el gráfico verse diferente si los datos representan las horas del día en que usted vive?
-
Tabla 1.5 Mes Promedio de horas de luz diurna Enero 5.65 Febrero 7.77 Marzo 10.4 Abril 13.37 Mayo 16.87 Junio 18.72 Julio 19.18 Agosto 17.12 Septiembre 14.27 Octubre 11.43 Noviembre 8.53 Diciembre 6.13
Revisar Respuestas [ editar ]
-
- (A) No es una función
- (B) ¿Es una función
- (C) No es una función
-
- (A) y = 95 x
- (B) La situación es variación directa.
- (c) 285 millas
-
- (A) C ( x ) = 2 x + 100
- (B) R ( x ) = 10 x
- (C) P ( x ) = 8 x - 100
- (D) Usted debe hacer y vender 13 marcos para obtener un beneficio.
-
- (La)

- (B) $ 15.63
- (La)
-
- (A) el beneficio máximo es de $ 3.850, con 90 unidades vendidas.
- (B) 2.25 y 177.75. Estos son los puntos de equilibrio. Cuando se venden 3.2 unidades, la compañía ha hecho suficiente dinero para compensar los costos iniciales.Después de la venta de 177 unidades, la empresa ya no es rentable.
Vocabulario [ editar ]
- variable dependiente
- La variable de entrada de una función, por lo general denota x .
- dominio
- El dominio es el conjunto de valores de entrada ( x ) para los que se define una función.
- función
- Una relación en la que cada elemento del dominio se empareja con exactamente un elemento de la gama.
- variable independiente
- La variable de salida de una función, por lo general denota y .
- función periódica
- Cualquier función que se repite regularmente.
- alcance
- El conjunto de la producción o los valores de función ( Y ) para una función.
- relación
- Un emparejamiento entre los artículos en dos conjuntos de números o datos.
- COODINATES es de dos puntos en el gráfico o función;




 , y la yes la constante de interceptación 1.
, y la yes la constante de interceptación 1.


 , los valores de la función se acercan a la x eje x ( y = 0).
, los valores de la función se acercan a la x eje x ( y = 0).
 etcétera
etcétera , los Y se acercan a los valores 0 ( x eje x).
, los Y se acercan a los valores 0 ( x eje x).



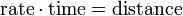






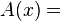









No hay comentarios:
Publicar un comentario