Triángulos y sus ángulos interiores [ editar ]
Formalmente, un triángulo se define como un polígono de 3 lados. Esto significa que un triángulo tiene 3 lados, todos los cuales son (rectas) segmentos de línea. Podemos clasificar los triángulos ya sea por sus lados, o por sus ángulos. La siguiente tabla resume los diferentes tipos de triángulos.
Tabla 1.6: Tipos de triángulos Nombre Descripción Nota Equilátero / equi-angular Un triángulo con tres lados iguales y tres ángulos congruentes. Este tipo de triángulo es agudo Isósceles Un triángulo con dos lados iguales y dos ángulos iguales. Un triángulo equilátero es también isósceles. Escaleno Un triángulo sin pares de lados iguales. Derecho Un triángulo con un ángulo de 90 °. No es posible para un triángulo de tener más de un ángulo de 90 ° (véase abajo). Agudo Un triángulo en el que los tres ángulos miden menos de 90 °. Obtuso Un triángulo en el que un ángulo es mayor que 90 °. No es posible para un triángulo de tener más de un ángulo obtuso (ver abajo).
En el siguiente ejemplo, vamos a clasificar los triángulos específicos.
Ejemplo 1
Determinar qué categoría describe mejor el triángulo:
a. Un triángulo con el lado longitudes de 3, 7 y 8.
b. Un triángulo con el lado de longitudes de 5, 5, y 5.
c. Un triángulo con el lado de longitudes de 3, 4, y 5.
Solución :
a. Este es un triángulo escaleno.
b. Este es un equilátero, o triángulo equiangular. También es aguda. c. Este es un triángulo escaleno, pero también es un triángulo rectángulo. |
Si bien existen diferentes tipos de triángulos, todos los triángulos tienen una cosa en común: la suma de los ángulos interiores de un triángulo es siempre 180 °. Usted puede ver por qué esto cierto si usted recuerda que una línea recta forma un "ángulo recto", que mide 180 °. Consideremos ahora el siguiente diagrama, que muestra el triángulo ABC , y una línea trazada a través del vértice B , paralela a lado AC . Por debajo de la cifra es una prueba de la suma de los ángulos del triángulo.
- Si tenemos en cuenta los lados AB y CB como transversales entre las líneas paralelas, a continuación, podemos ver que el ángulo A y el ángulo 1 son ángulos alternos internos.
- Del mismo modo, el ángulo C y el ángulo 2 son ángulos alternos.
- Por lo tanto el ángulo A y el ángulo 1 son congruentes, y el ángulo C y el ángulo 2 son congruentes.
- Ahora cuenta que los ángulos 1, 2 y B forman una línea recta. Por lo tanto la suma de los tres ángulos es 180 °.
- Podemos completar la prueba usando substitución:
Podemos utilizar este resultado para determinar la medida de los ángulos de un triángulo. En particular, si conocemos las medidas de dos ángulos, siempre podemos encontrar el tercero.
Ejemplo 3
Encuentra las medidas de los ángulos que faltan.
a. Un triángulo tiene dos ángulos que miden 30 ° y 50 °.
b. Un triángulo rectángulo tiene un ángulo que mide 30 °.
c. Un triángulo isósceles tiene un ángulo que mide 50 °.
Solución :
a. 100 °
180-30 - 50 = 100
b. 60 °
El triángulo es un triángulo rectángulo, lo que significa que un ángulo mide 90 °.
Así que tenemos 180 - 90 - 30 = 60
c. 50 ° y 80 ° o 65 ° y 65 °
Hay dos posibilidades. En primer lugar, si un segundo ángulo mide 50 °, entonces el tercer ángulo mide 80 ° como 180-50 - 50 = 80.
En el segundo caso, el ángulo de 50 ° no es uno de los ángulos congruentes. En este caso, la suma de los otros dos ángulos es 180-50 = 130. Por lo tanto los dos ángulos cada medida de 65 °.
|
Nótese que la información sobre los ángulos de un triángulo no nos dicen las longitudes de los lados. Por ejemplo, dos triángulos podría tener el mismo tres ángulos, pero no los triángulos son congruentes. Es decir, los lados correspondientes y los ángulos correspondientes no tienen las mismas medidas. Sin embargo, estos dos triángulos serán similares. Siguiente definimos similitud y discutir los criterios de triángulos sean similares.
Triángulos similares [ editar ]
Tenga en cuenta la situación en la que dos triángulos tienen tres pares de ángulos congruentes.
Estos triángulos son semejantes. Esto significa que los ángulos correspondientes son congruentes, y los lados correspondientes son proporcionales. En los triángulos aparecen arriba, tenemos lo siguiente:
- Tres pares de ángulos congruentes:

- Las relaciones de lados dentro de un triángulo son iguales a las proporciones de cada lado dentro de la segunda triángulo:

- Las proporciones de los lados correspondientes son iguales:

Ejemplo 4
|
Recordemos que estos triángulos se considera que ser similares porque tienen tres pares de ángulos congruentes. Esta es sólo una de las tres formas de determinar que dos triángulos son semejantes. La siguiente tabla resume los criterios para determinar si dos triángulos son semejantes.
Un caso especial de SSS es "HL", o "la pierna hipotenusa". Este es el caso de dos triángulos rectángulos ser similar. Este caso se examina en el ejemplo 5 a continuación.
Ejemplo 5
Determinar si los triángulos son semejantes.
Solución :
Los triángulos son semejantes.
Recordemos que por cada triángulo rectángulo, podemos usar el teorema de Pitágoras para encontrar la longitud de un lado que falta. En ABC tenemos:
Del mismo modo, en el triángulo DEF tenemos:
Por lo tanto los lados de los triángulos son proporcionales, con una relación de 2: 1.
|
Debido a que siempre vamos a poder utilizar el Teorema de Pitágoras de esta manera, dos triángulos rectángulos serán similares si la hipotenusa y una pierna de un triángulo son proporcionales a la hipotenusa y una pierna del segundo triángulo. Este es el criterio HL.
Aplicaciones de triángulos similares [ editar ]
Triángulos similares se pueden utilizar para resolver problemas en los que longitudes o distancias son proporcionales. El siguiente ejemplo le mostrará cómo resolver este tipo de problemas.
Ejemplo 6
Use triángulos semejantes para resolver el problema:
Un árbol proyecta una sombra que es de 24 pies de largo. Una persona que es de 5 pies de altura está de pie delante del árbol y su sombra es de 8 pies de largo.Aproximadamente, ¿es la altura del árbol?
Solución :
La imagen nos muestra triángulos semejantes correctas: la persona y su sombra son las piernas de un triángulo, y el árbol y su sombra forman los catetos del triángulo más grande. Los triángulos son similares debido a sus ángulos: los dos tienen un ángulo recto, y comparten un ángulo. Por lo tanto los ángulos tercero también son congruentes, y los triángulos son similares.
La relación de las longitudes de los triángulos 'es de 3: 1. Si dejamos que h representamos la altura del árbol, tenemos:
|
Resumen de la lección [ editar ]
En esta lección hemos revisado los aspectos clave de triángulos, incluyendo los nombres de los diferentes tipos de triángulos, la suma de los ángulos del triángulo, y los criterios de triángulos semejantes. En el último ejemplo, utilizamos triángulos semejantes para resolver un problema que involucra una altura desconocida. En general, los triángulos son útiles para resolver este tipo de problemas, pero advierten que no usamos los ángulos de los triángulos para resolver este problema. Esta técnica será el tema central de los problemas que va a resolver más adelante en el capítulo.
Puntos a considerar [ editar ]
- ¿Por qué es imposible que un triángulo de tener más de un ángulo recto?
- ¿Por qué es imposible que un triángulo de tener más de un ángulo obtuso?
- ¿Qué tan grande puede obtener la medida de un ángulo?
Preguntas de repaso [ editar ]
- Triángulo ABC es un triángulo isósceles. Si el lado AB es de 5 pulgadas de largo, y el lado BC es de 7 pulgadas de largo, ¿cuánto tiempo es el lado de CA ?
- ¿Puede un triángulo rectángulo es un triángulo obtuso? Explique.
- Un triángulo tiene un ángulo que mide 48 ° y un segundo ángulo que mide 28 °. ¿Cuál es la medida del tercer ángulo del triángulo?
- Reclamo: los dos ángulos no rectos en cualquier triángulo rectángulo son complementos.
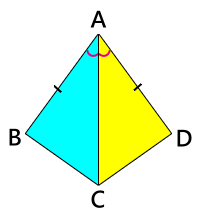
- En el triángulo DOG , la medida del ángulo O es el doble de la medida del ángulo D , y la medida del ángulo G es tres veces la medida del ángulo D . ¿Cuáles son las medidas de los tres ángulos?
- Los triángulos ABC y DEF se muestran a continuación son similares. ¿Cuál es la longitud de
 ?
?
- En los triángulos ABC y DEF anterior, si el ángulo A mide 30 °, ¿cuál es la medida del ángulo E ?
- Determinar si los triángulos son semejantes:
- Un edificio proyecta una sombra de 100 pies, mientras que un mástil de 20 pies al lado del edificio proyecta una sombra de 24 pies. ¿Qué altura tiene el edificio?
- Explique en sus propias palabras lo que significa para los triángulos sean similares.
Revisar Respuestas [ editar ]
- Cualquiera de 5 pulgadas o 7 pulgadas.
- Un triángulo rectángulo no puede ser un triángulo obtuso. Si un triángulo es triángulo rectángulo, un ángulo mide 90 grados. Si un triángulo es obtuso, un ángulo mide mayor que 90. Por lo tanto la suma de los dos ángulos sería mayor que 180 grados, lo que no es posible.
- 104 °
-
- (A) La suma de los ángulos en el triángulo es 180. Si se resta el ángulo de 90 grados, tienes 180-90 = 90 grados, que es la suma de los ángulos restantes.
- (B) 90-23 = 67 °


- 7.5
- 130 °
-
- (A) Ninguna
- (B) Sí, por SSS o HL
- 83
 ft
ft - Las respuestas pueden variar. Las respuestas deben incluir (1) tres pares de ángulos congruentes y (2) las partes en proporción, o algún otro concepto de "ampliación" o "escalar hacia abajo".
Vocabulario [ editar ]
- ángulo agudo
- Un ángulo agudo tiene una medida de menos de 90 grados.
- congruente
- Dos ángulos son congruentes si tienen la misma medida. Dos segmentos son congruentes si tienen la misma longitud.
- triángulo agudo
- Un triángulo con todos los ángulos agudos.
- triángulo isósceles
- Un triángulo con dos lados congruentes y, Consecuentemente, los dos ángulos congruentes.
- triángulo equilátero
- Un triángulo con todos los lados congruentes, y, por consiguiente, todos los ángulos congruentes.
- triángulo escaleno
- Un triángulo sin pares de lados congruentes.
- pierna
- Uno de los dos lados más cortos de un triángulo rectángulo.
- hipotenusa
- El lado más largo de un triángulo rectángulo, opuesto al ángulo recto.
- ángulo obtuso
- Un ángulo que mide más de 90 grados.
- lineas paralelas
- Las líneas que nunca se cruzan.
- ángulo recto
- Un ángulo que mide 90 grados.
- transversal
- Una línea que se cruza líneas paralelas.

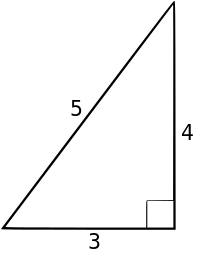




 . ¿Cuáles son las longitudes de los lados DF y EF ?
. ¿Cuáles son las longitudes de los lados DF y EF ?
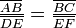 tenemos
tenemos 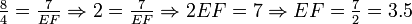 .
. tenemos
tenemos  .
.







No hay comentarios:
Publicar un comentario