martes, 30 de junio de 2015

Trigonometría

Funciones trigonométricas

En trigonometría, la tangente (abreviado tan) de un ángulo (en un triángulo rectángulo) se define como la razón entre el cateto opuesto y el adyacente:
\tan(\alpha) = \frac{a}{b}
O también como la relación entre el seno y el coseno:
\tan(\alpha) = \frac{sen(\alpha) }{\cos(\alpha) } \,

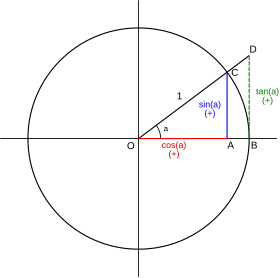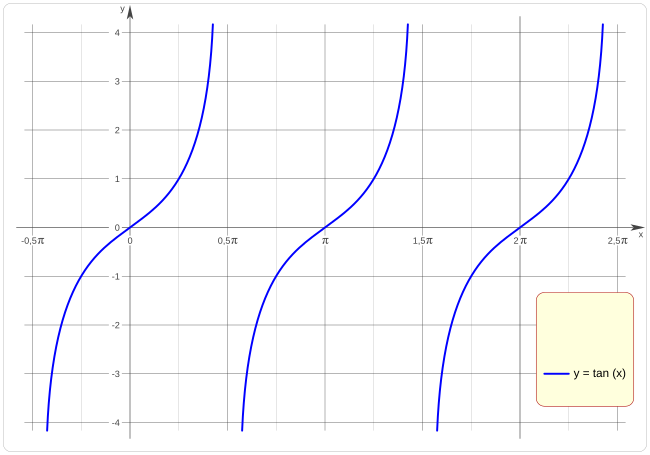
Representación en un círculo unitario el seno, coseno y la tangente de un ángulo.

Representación gráfica

Función Trigonométrica R001.svg

Identidades

Artículo principal: Identidades trigonométricas

Tangente de la suma de dos ángulos[editar]

Esta identidad trigonométrica parte de la identidad de la suma de dos ángulos ya conocida para el seno y el coseno.
  • Dados los ángulos  \phi,\theta\ :
\tan\left(\phi+\theta\right) = \cfrac{\sen(\phi+\theta)}{\cos(\phi+\theta)}
  • Reemplazando por las identidades antes mencionadas:
\tan\left(\phi+\theta\right) = \cfrac{ \sen \phi \cos \theta + \cos \phi \sen \theta }{ \cos \phi \cos \theta - \sen \phi \sen \theta }
  • Dividiendo al numerador y al denominador por \cos\phi\cos\theta\,:
\tan \left( \phi + \theta \right) = \cfrac{ \cfrac{ \sen \phi \cos \theta + \cos \phi \sen \theta }{ \cos \phi \cos \theta } }{ \cfrac{ \cos\phi\cos\theta-\sen\phi\sen\theta }{ \cos\phi\cos\theta } }
  • Separando la suma y la resta:
\tan \left( \phi + \theta \right) = \cfrac{ \cfrac{ \sen\phi\cos\theta }{ \cos\phi\cos\theta } + \cfrac{ \cos\phi\sen\theta }{ \cos\phi\cos\theta } }{ \cfrac{ \cos\phi\cos\theta }{ \cos\phi\cos\theta } - \cfrac{ \sin\phi\sen\theta }{ \cos\phi\cos\theta } }
  • Simplificando cada fracción:
\tan \left( \phi + \theta \right) = \cfrac{ \cfrac{ \sen \phi }{ \cos \phi } + \cfrac{ \sen \theta }{ \cos \theta } }{ 1 - \cfrac{ \sen \phi \sen \theta }{ \cos \phi \cos \theta } }
  • Reemplazando las fracciones de seno y coseno por tangente, se obtiene:
\tan \left( \phi + \theta \right) = \cfrac{ \tan \phi + \tan \theta }{ 1 - \tan \phi \tan \theta }

Tangente de la diferencia de dos ángulos[editar]

  • \tan \left( \phi + (- \theta) \right) = \frac{ \tan \phi + \tan (-\theta) }{ 1 - \tan \phi \tan (-\theta) }
\tan \left( \phi - \theta \right) = \frac{ \tan \phi - \tan \theta }{ 1 + \tan \phi \tan \theta }

Forma resumida[editar]

\tan\left(\phi\pm\theta\right)=\frac{\tan\phi\pm\tan\theta}{1\mp\tan\phi\tan\theta}

Tangente de un ángulo doble[editar]

  • \tan \left( \phi + \theta \right) = \frac{ \tan \phi + \tan \theta }{ 1 - \tan \phi \tan \theta }
  • Haciendo 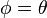\phi=\theta\, entonces:
\tan \left( 2 \phi \right) = \frac{ 2 \tan \phi }{ 1 - \tan^2 \phi }



La función verseno (en Latín, sinus versus o sagitta, flecha) es una función trigonométrica que se define con la ecuación
\textrm{versin} (\theta) = 1 - \cos (\theta) = 2\ \text{sen}^2\left(\frac{\theta} {2}\right) \,
Existen tres funciones relacionadas con el verseno:
El coverseno:
\textrm{coversin}(\theta) = \textrm{versin}\left(\frac{\pi}{2} - \theta\right) = 1 - \text{sen}(\theta) \,
El semiverseno:
\textrm{semiversin}(\theta) = \frac {\textrm{versin}(\theta)} {2} = \text{sen}^2\left(\frac {\theta} {2} \right)
El semicoverseno:
\textrm{semicoversin}(\theta) = \textrm{semiversin}\left(\frac{\pi}{2} - \theta\right) = \frac {\textrm{coversin}(\theta)} {2}



Históricamente, el verseno fue considerado una de las funciones trigonométricas más importantes, pero ha perdido renombre en los tiempos modernos debido a la disponibilidad de los ordenadores. Si θ tiende a cero, versen(θ) es la diferencia entre dos cantidades muy parecidas, y sería preciso una tabla trigonométrica muy exacta para poder calcular el verseno, eso hace conveniente la creación de tablas separadas para el verseno. Otra ventaja histórica del verseno es que nunca es negativo, así, su logaritmo está definido en todas partes excepto de θ = 0, 2π,... permitiendo así usar tablas de logaritmos para calcular las multiplicaciones en las fórmulas que impliquen verseno.
El semiverseno, en particular, fue importante en navegación debido a que aparece en la fórmula del semiverseno, usada para calcular distancias con exactitud cuando se dan las posiciones angulares en una esfera (la longitud y la latitud).
La tabla trigonométrica más antigua que se conserva, de entre los siglos IV y V, llamada Siddhantas y proveniente de la India, sólo tenía valores del seno y del verseno (en incrementos de 3.75° desde 0 hasta 90°). Eso no es sorprendente dado que el verseno resulta de un paso intermedio para calcular el seno del ángulo mitad según la fórmula sin2(θ/2) = versen(θ)/2, que se atribuye a Ptolomeo.
seno, coseno, y verseno de θ en base a la circunferencia goniométrica.
El significado de la palabra verseno está reflejado en la definición gráfica de la circunferencia goniométrica que se muestra en la imagen. La cuerda vertical AB de la circunferencia goniométrica, el seno del ángulo θ es la distancia AC (la mitad de la cuerda). El verseno de θ es la distancia CD desde el centro del arco al centro de la cuerda (del arco hacia el seno) o dicho por Fibonacci en latín ‘'sinus versus arcus‘'.
Esta figura también ilustra el motivo por el que al verseno a menudo también se le llama flecha. El verseno “CD” es claramente la flecha entre la cuerda y el arco.
La forma de onda de un periodo de la función verseno y, más habitualmente, la de la función semiverseno, se usan habitualmente en procesado de señal y en teoría de control como la forma de una ventana de observación, debido a su suavidad (continuidad tanto en valor como en pendiente (primera derivada). En estas aplicaciones, se le llama también filtro del coseno realzado.

El término verseno también se usa a veces para describir la desviación de una curva plana cualquiera respecto de la recta. Dada unacuerda entre dos puntos de una curva, la longitud desde un punto de la cuerda hasta el punto donde la perpendicular a la cuerda corta la curva, da el verseno. Para una línea recta, el verseno de cualquier cuerda es cero. Así el verseno caracteriza la rectitud de la curva. Este uso es habitual en el ferrocarril, donde sirve para medir la rectitud o curvatura de la vía férrea (Nair, 1972).
Publicado por en

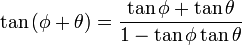
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)