Aplicaciones de Radian Medida
Rotaciones [ editar ]
Ejemplo 1
Las manecillas de un reloj muestran 11:20. Expresar el ángulo obtuso formado por las horas y los minutos en radianes a la décima de un radián.
El siguiente diagrama muestra la ubicación de las manos a la hora especificada.
Solución :
Debido a que hay 12 incrementos de un reloj, el ángulo entre cada hora que marca el reloj es
 = =  (o 30 °). Por lo tanto, el ángulo entre el 12 y el 4 es 4 · (o 30 °). Por lo tanto, el ángulo entre el 12 y el 4 es 4 ·  = = 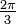 (o 120 °).Debido a la rotación 12-4 es una tercera parte de una rotación completa, parece razonable suponer que la manecilla de las horas está moviendo continuamente y por lo tanto se ha movido un tercio de la distancia entre la 11 y la 12. Por lo tanto, (o 120 °).Debido a la rotación 12-4 es una tercera parte de una rotación completa, parece razonable suponer que la manecilla de las horas está moviendo continuamente y por lo tanto se ha movido un tercio de la distancia entre la 11 y la 12. Por lo tanto,  · ·  = =  , y la medida total del ángulo, por lo tanto es , y la medida total del ángulo, por lo tanto es  + + 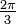 = =  + +  = =  . El uso de una calculadora para aproximar el ángulo daría: . El uso de una calculadora para aproximar el ángulo daría:
14π / 18
2.44346
Para el décimo más cercano de un radián es 2,4 radianes.
|
Longitud de un arco [ editar ]
La longitud de un arco en un círculo depende tanto el ángulo de rotación y la longitud del radio del círculo. Si recuerdan desde la última lección, definimos un radián como la longitud del arco de la medida de un ángulo θ en radianes se define como la longitud del arco cortada por una longitud del radio, de modo que una media-rotación es π radianes , o un poco más de 3 longitudes de radio alrededor del círculo. ¿Qué pasa si el radio es 4 cm? La longitud del arco de medio círculo se π longitudes RADIUS o 4π cm de longitud.
Esto resulta en una fórmula que se puede utilizar para calcular la longitud de cualquier arco.
donde s es la longitud del arco, r es el radio, y θ es la medida del ángulo en radianes.
Resolviendo esta ecuación para θ nos dará una fórmula para encontrar la medida radián dada la longitud del arco y la longitud del radio:
Ejemplo 2
La línea de tiros libres en una cancha de baloncesto de la NCAA es de 12 pies de ancho. En la competencia internacional, es sólo alrededor de 11.81 pies. ¿Cuánto tiempo es el medio círculo por encima de la línea de tiro libre en la cancha de la NCAA?
Solución :
Arco cálculos de longitud:
Así que la respuesta es aproximadamente 6π - 5.905π ≈ 0.095π.
.095π
.0.29845130209103
Esto es aproximadamente 0,3 pies, o alrededor de 3,6 pulgadas más largo.
|
Ejemplo 3
Dos engranajes conectados están girando. El engranaje más pequeño tiene un radio de 4 pulgadas y el radio del engranaje más grande es de 7 pulgadas. ¿Cuál es el ángulo a través del cual el engranaje más grande ha girado cuando el engranaje más pequeño ha hecho una rotación completa?
Solución :
Debido a que el engranaje azul realiza una rotación completa, la longitud del arco recorrida es:
Por lo tanto, una longitud de arco 8π en el círculo más grande sería formar un ángulo como sigue:
Así que el ángulo es de aproximadamente 3,6 radianes.
|
Área de un sector [ editar ]
Una de las fórmulas geométricas más comunes es el área de un círculo:
En cuanto a la rotación de ángulo, este es el área creada por 2π radianes.
Un semicírculo, o la rotación en radianes π crearían una sección o sector del círculo igual a la mitad del área o:
Así un ángulo de 1 radián definiría un área de un sector igual a:
De esto podemos determinar el área del sector creado por cualquier ángulo, θ radianes, sean:
Ejemplo 4
Los cultivos se cultivan a menudo usando una técnica llamada riego de pivote central que resulta en campos de forma circular.
Aquí está una imagen de satélite tomada campos en Kansas que utilizan este tipo de sistema de riego.
Si la tubería de riego es de 450 m de longitud, lo que es el área que puede ser irrigado después de una rotación de
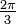 radianes? radianes?
Solución :
Utilizando la fórmula:
0,5 * 450 2 * 2π / 3
212057.5041
El área es de aproximadamente 212.058 metros cuadrados.
|
Longitud de un acorde [ editar ]
Usted puede recordar de sus Geometría estudios que un acorde es un segmento que comienza y termina en un círculo.
 es un acorde en el círculo.
es un acorde en el círculo.
Podemos calcular la longitud de cualquier acorde si conocemos la medida del ángulo y la longitud del radio. Debido a que cada punto final de la cuerda es en el círculo, la distancia desde el centro de A y B es la misma que la longitud del radio.
A continuación, si bisecan el ángulo, la bisectriz del ángulo debe ser perpendicular a la cuerda (vamos a dejar la prueba de esto a su clase de geometría). Esto forma un triángulo rectángulo.
Ahora podemos usar una relación sinusoidal simple de encontrar un medio acorde, llamado c aquí, y duplicar el resultado para encontrar la longitud de la cuerda.
Así que la longitud de la cuerda es:
Ejemplo 5
Encuentra la longitud de la cuerda de un círculo con un radio de 8 cm y un ángulo central de 110 °. Aproxime su respuesta al mm más cercano.
Solución :
Siempre es una buena técnica de resolución de problemas para estimar la respuesta primero. Un proceso de pensamiento para la estimación de la medida podría ser algo como esto:
El ángulo es ligeramente más de 90 °, o
 radianes. radianes.  radianes es ligeramente más de 1,5 longitudes de radio. Radios y medio serían 12, por lo que podrían esperar la respuesta a ser un poco más de 12 cm. Vamos a ver cómo se compara la respuesta real. radianes es ligeramente más de 1,5 longitudes de radio. Radios y medio serían 12, por lo que podrían esperar la respuesta a ser un poco más de 12 cm. Vamos a ver cómo se compara la respuesta real.
Primero debemos convertir la medida del ángulo en radianes:
Utilizando la fórmula, la mitad de la longitud de la cuerda debe ser el radio de las veces en círculo el seno de la mitad del ángulo.
8 · pecado
 (Asegúrese de que su calculadora está en radianes!) (Asegúrese de que su calculadora está en radianes!)
Multiplique este resultado por 2.
8sin (11π / 36)
6.553216354
Ans * 2
13.10643271
Por lo tanto, la longitud del arco es aproximadamente 13,1 cm. Esto parece muy razonable basada en nuestra estimación.
|
Preguntas de repaso [ editar ]
- La imagen de la derecha muestra un reloj de 24 horas en Curitiba, Paraná, Brasil.
- (A) ¿Cuál es el ángulo entre cada número del reloj expresado en:
- yo. radianes exacta en términos de π?
- ii. al décimo más cercano de un radián?
- iii. en medida en grados?
- (B) Estimar la medida del ángulo entre las manos en el momento se muestra en:
- yo. al grado entero más cercano
- ii. en radianes en términos de π
- (A) ¿Cuál es el ángulo entre cada número del reloj expresado en:
-
La imagen de la derecha es una ventana de un edificio en el campus de la Universidad de Princeton en Princeton, Nueva Jersey.
- (A) ¿Cuál es la medida radián exacta en términos de π entre dos puntos circulares consecutivos en el pequeño círculo en el centro de la ventana?

- (B) Si el radio de este círculo es de aproximadamente 0,5 m, lo que es la longitud del arco entre los centros de cada punto consecutivo? Redondea tu respuesta al cm más cercano.

- Ahora mira el siguiente círculo más grande en la ventana.

- (A) Hallar la medida radián exacta en términos de π entre dos puntos consecutivos en esta ventana.
- (B) El radio de la parte de cristal de esta ventana es de aproximadamente 1,20 m. Calcula una estimación de la longitud de la cuerda resaltado al cm más cercano.Explicar el razonamiento detrás de su solución.

- El partido por el campeonato del estado es que se celebrará en Ray Díaz Memorial Arena. Los asientos se forma un círculo perfecto alrededor de la cancha. El director de la Escuela Secundaria de Arquímedes se envía el siguiente diagrama que muestra los asientos asignados a los estudiantes en su escuela. Es 55 pies desde el centro de la cancha hasta el principio de los stands y 110 pies desde el centro hasta el final. Calcular el número aproximado de pies cuadrados cada uno de los siguientes grupos se ha concedido:

- (A) los estudiantes de Arquímedes
- (B) la entrada general
- (C) la prensa y funcionarios
-
A la derecha hay una imagen de la bandera del estado de Colorado. Resulta que el diámetro del círculo de oro es
 la altura total de la bandera (la misma anchura que la raya amarilla) y el diámetro exterior del círculo rojo es
la altura total de la bandera (la misma anchura que la raya amarilla) y el diámetro exterior del círculo rojo es  de la altura total de la bandera. El ángulo formado por la porción que falta de la banda de rojo es
de la altura total de la bandera. El ángulo formado por la porción que falta de la banda de rojo es  radianes. En una bandera que es de 33 pulgadas de alto, lo que es el área de la parte roja de la bandera por pulgada cuadrada más cercana?
radianes. En una bandera que es de 33 pulgadas de alto, lo que es el área de la parte roja de la bandera por pulgada cuadrada más cercana?
Revisar Respuestas [ editar ]
-
- (A) i.

- ii. ≈ 0,3 radianes
- iii. 15
- (B) i. 20 °. Las respuestas pueden variar, nada de 15 ° y menos de 25 ° es razonable.
- ii.
 . Una vez más, las respuestas pueden variar.
. Una vez más, las respuestas pueden variar.
- (A) i.
-
- (La)

- (B) ≈ 26 cm
- (La)
-
- (La)

- (B) Supongamos, para simplificar, que la cuerda se extiende hasta el centro de cada uno de los puntos. Tenemos que encontrar la medida del ángulo central del círculo que conecta los dos puntos. Puesto que hay 13 puntos, este ángulo es . La longitud de la cuerda entonces es:

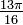


- 2 * 1.2sin (13π / 32)2.296656806
- El acorde es de aproximadamente 2,30 cm.
- (La)
- Cada sección es
 radianes. Por consiguiente, el área de una sección de las gradas es el área del sector exterior menos el área del sector interior:
radianes. Por consiguiente, el área de una sección de las gradas es el área del sector exterior menos el área del sector interior:
- (A) Los estudiantes tienen cuatro secciones o ≈ 9.503 pies 2
- (B) Hay tres secciones de admisión general o ≈ 7.127 pies 2
- (C) Sólo hay una prensa y funcionarios de sección o ≈ 2.376 pies 2
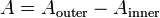


- 0,5 * 110 2 * π / 6-0,5 * 55 2
* π / 62375.829444 - El área de cada sección es de aproximadamente 2.376 ft 2 .
- Hay muchos enfoques diferentes para el problema. He aquí una posibilidad:
- En primer lugar, calcular el área del anillo rojo como si se fue por completo alrededor del círculo:

- A continuación, calcular el área del total del sector que formaría la apertura de la "c":

- A continuación, se calcula el área del sector amarillo y restarlo de la respuesta anterior.
- Por último, restar esta respuesta de la primera área calculada.
- El área es de aproximadamente 998 en 2 .
- En primer lugar, calcular el área del anillo rojo como si se fue por completo alrededor del círculo:







 ≈ 206 °
≈ 206 °




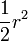





























No hay comentarios:
Publicar un comentario