Funciones trigonométricas
arcocosecante es la función inversa de lacosecante de un ángulo. Se simboliza  ó
ó  y su significado geométrico es el ángulo cuya cosecante es alfa.
y su significado geométrico es el ángulo cuya cosecante es alfa.
 ó
ó  y su significado geométrico es el ángulo cuya cosecante es alfa.
y su significado geométrico es el ángulo cuya cosecante es alfa.
De esta definición, por tanto, podemos deducir expresiones equivalentes:
La notación habitual de la función arcocosecante es 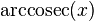 ó
ó  . También es válida la notación cosec-1 (leído comocosecante a la menos uno). Esta última notación no suele estar aconsejada debido a su ambigüedad, ya que es susceptible de ser confundida con una potencia de exponente -1, y su uso es habitual en Norteamérica y en las calculadoras de bolsillo.
. También es válida la notación cosec-1 (leído comocosecante a la menos uno). Esta última notación no suele estar aconsejada debido a su ambigüedad, ya que es susceptible de ser confundida con una potencia de exponente -1, y su uso es habitual en Norteamérica y en las calculadoras de bolsillo.
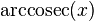 ó
ó  . También es válida la notación cosec-1 (leído comocosecante a la menos uno). Esta última notación no suele estar aconsejada debido a su ambigüedad, ya que es susceptible de ser confundida con una potencia de exponente -1, y su uso es habitual en Norteamérica y en las calculadoras de bolsillo.
. También es válida la notación cosec-1 (leído comocosecante a la menos uno). Esta última notación no suele estar aconsejada debido a su ambigüedad, ya que es susceptible de ser confundida con una potencia de exponente -1, y su uso es habitual en Norteamérica y en las calculadoras de bolsillo.
En el lenguaje LaTeX esta expresión se obtiene mediante el comando \arccsc.
La cosecante inversa es la función de varios valores  (Zwillinger 1995, p 465.), también denota
(Zwillinger 1995, p 465.), también denota  (Abramowitz y Stegun 1972, p 79;. Spanier y Oldham 1987, p 332;. Harris y Stocker 1998, p 315;. Jeffrey 2000, p . 125), que es la función inversa de la cosecant . Las variantes
(Abramowitz y Stegun 1972, p 79;. Spanier y Oldham 1987, p 332;. Harris y Stocker 1998, p 315;. Jeffrey 2000, p . 125), que es la función inversa de la cosecant . Las variantes  (por ejemplo, Beyer 1987, p 141;.. Bronshtein y Semendyayev, 1997, p 70) y
(por ejemplo, Beyer 1987, p 141;.. Bronshtein y Semendyayev, 1997, p 70) y  se utilizan a veces para referirse a explícitos los valores principales de la cosecante inversa, aunque esta distinción no siempre se hace (por ejemplo ,. Zwillinger 1995 ,. p 466). Peor aún, la notación
se utilizan a veces para referirse a explícitos los valores principales de la cosecante inversa, aunque esta distinción no siempre se hace (por ejemplo ,. Zwillinger 1995 ,. p 466). Peor aún, la notación  se utiliza a veces para el valor principal, con
se utiliza a veces para el valor principal, con  que se utiliza para la función de varios valores (Abramowitz y Stegun 1972, p. 80). Tenga en cuenta que en la notación
que se utiliza para la función de varios valores (Abramowitz y Stegun 1972, p. 80). Tenga en cuenta que en la notación  (de uso común en América del Norte y en las calculadoras de bolsillo en todo el mundo),
(de uso común en América del Norte y en las calculadoras de bolsillo en todo el mundo),  es la cosecante y el superíndice
es la cosecante y el superíndice  denota una función inversa , no el inverso multiplicativo.
denota una función inversa , no el inverso multiplicativo.
La cosecante inversa es una función de varios valores y por lo tanto requiere de una rama cortada en el plano complejo , que el idioma Wolframconvención 's coloca en  . Esto se deduce de la definición de
. Esto se deduce de la definición de  lo
lo
(1)
|
El derivado de  está dada por
está dada por
(2)
|
lo que simplifica a
(3)
|
para  . Su integral indefinida es
. Su integral indefinida es
(4)
|
lo que simplifica a
(5)
|
para  .
.
La cosecante inversa tiene serie de Taylor sobre infinidad de
(6)
| |||
(7)
| |||
(8)
|
Las satisface cosecante inversa
(9)
|
para  ,
,
(10)
| |||
(11)
|
para todos complejo  , y
, y
(12)
| |||
(13)
| |||
La derivada del arcocosecante de una función es igual a menos la derivada de la función dividida por la función multiplicada por la raíz cuadrada del cuadrado de la función menos 1.
Inverso de la función cosecante. También se escribe arco cosecante, arc cosec x, o cosec-1. El valor de la función arco cosecante de cualquier argumento es un ángulo en radianes cuya función cosecante es igual al argumento dado, esto es, y = csc-1x si y sólo si x = cosec(y) para -
|


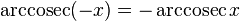
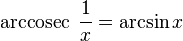
 y
y  o entre
o entre  y
y  .
.
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
No hay comentarios:
Publicar un comentario