Funciones trigonométricas
El Secante, (abreviado como sec), es la razón trigonométrica recíproca del coseno, o también su inverso multiplicativo:

Explicación
Sabiendo que
Según la figura: los triángulos ABC rectángulo en C y ADE rectángulo en E son semejantes, por lo que tenemos que:
La distancia AE vale uno porque E esta en la circunferencia, luego:
Lo que resulta:
El segmento AD es la secante, en una circunferencia de radio uno.
Representación gráfica
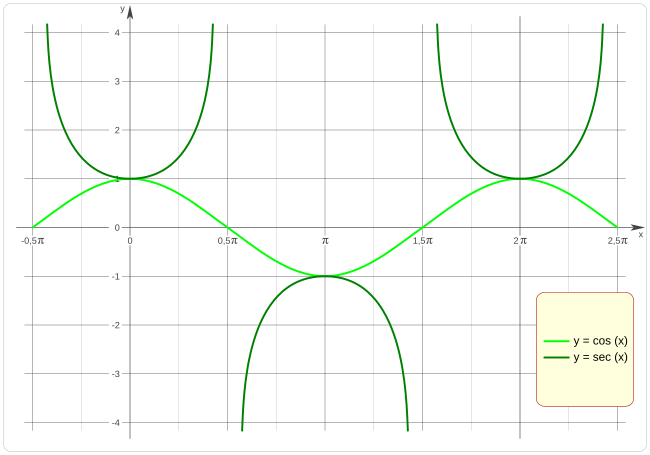
y=sec(x)
Coseno y secante de un ángulo
Partiendo de la definición de secante como la inversa del coseno:
Conociendo la función coseno, podemos ver que para los valores en los que el coseno vale cero, la secante se hace infinito, si la función coseno tiende a cero desde valores positivos la secante tiende a:  .
.
 .
.
mientras que cuando el coseno tiende a cero desde valores negativos la secante tiende a:  .
.
 .
.
Cuando el coseno del ángulo vale uno, su secante también vale uno, como se puede ver en la gráfica.
La secante del ángulo B es la razón inversa del coseno de B.
Se denota por sec B.
Secante en la circunferencia goniométrica
Signo de la secante
Relación entre la secante y la tangente
sec² α = 1 + tg² α
Ejemplo
Sabiendo que tg α = 2, y que 180º < α <270 calcular="" de="" la="" p="" secante="">

En un triángulo rectángulo, es la longitud de la hipotenusa dividida para la longitud del lado adyacente.
La abreviatura es sec
Ejemplo: en un triángulo con lados de 3, 4 y 5, la secante de el ángulo donde los lados de longitud 4 y 5 se encuentran es 5/4.
No es comúnmente usada, y es igual a 1/coseno
==> Coseno
Secante (función)
En un triángulo rectángulo, es la longitud de la hipotenusa dividida para la longitud del lado adyacente.
La abreviatura es sec
Ejemplo: en un triángulo con lados de 3, 4 y 5, la secante de el ángulo donde los lados de longitud 4 y 5 se encuentran es 5/4.
No es comúnmente usada, y es igual a 1/coseno
==> Coseno
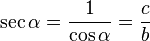










No hay comentarios:
Publicar un comentario