AMIGOS PARA SIEMPRE: Trigonometría

Funciones trigonométricas

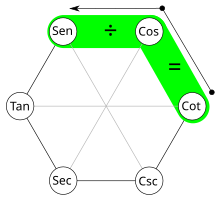
El hexágono trigonométrico es un recurso mnemónico para ayudar a recordar relaciones e identidades trigonométricas. Las primeras versiones del hexágono aparecieron en una publicación china "Mathematics Handbook" en 1978.

Identidades pitagóricas

	$\sen^2 \theta + \cos^2 \theta = 1$
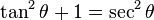	$\tan^2 \theta + 1 = \sec^2 \theta$
	$1 + \cot^2 \theta = \csc^2 \theta$

Identidades recíprocas

Cada función trigonométrica es el recíproco de la que está en el lado opuesto del hexágono.

	$\sen \theta = 1 / \csc \theta$	$\csc \theta = 1 / \sen \theta$
	$\cos \theta = 1 / \sec \theta$	$\sec \theta = 1 / \cos \theta$
	$\tan \theta = 1 / \cot \theta$	$\cot \theta = 1 / \tan \theta$

Productos

El producto de cada función trigonométrica multiplicada por la opuesta en el hexágono es 1.

	$\sen \theta * \csc \theta = 1$	$\csc \theta * \sen \theta = 1$
	$\cos \theta * \sec \theta = 1$	$\sec \theta * \cos \theta = 1$
	$\tan \theta * \cot \theta = 1$	$\cot \theta * \tan \theta = 1$

Cada función trigonométrica es el producto de las dos que la rodean.

	$\sen \theta = \tan \theta * \cos \theta$	$\csc \theta = \cot \theta * \sec \theta$
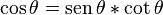	$\cos \theta = \sen \theta * \cot \theta$	$\sec \theta = \csc \theta * \tan \theta$
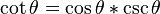	$\tan \theta = \sec \theta * \sen \theta$	$\cot \theta = \cos \theta * \csc \theta$

Cocientes

Cada función trigonométrica es el cociente de las dos siguientes.

	$\sen \theta = \cos \theta / \cot \theta$	$\csc \theta = \sec \theta / \tan \theta$
	$\cos \theta = \cot \theta / \csc \theta$	$\sec \theta = \tan \theta / \sen \theta$
	$\tan \theta = \sen \theta / \cos \theta$	$\cot \theta = \csc \theta / \sec \theta$

Cada función trigonométrica es el cociente de las dos anteriores.

	$\sen \theta = \tan \theta / \sec \theta$	$\csc \theta = \cot \theta / \cos \theta$
	$\cos \theta = \sen \theta / \tan \theta$	$\sec \theta = \csc \theta / \cot \theta$
	$\tan \theta = \sec \theta / \csc \theta$	$\cot \theta = \cos \theta / \sen \theta$

Identidades de la cofunción

Cada función trigonométrica de un ángulo dado

\theta

es igual a su cofunción evaluada en

\left( \frac{\pi}{2} - \theta \right)

	$\sen \theta = \cos \left( \frac{\pi}{2} - \theta \right)$	$\cos \theta = \sen \left( \frac{\pi}{2} - \theta \right)$
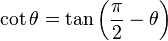	$\tan \theta = \cot \left( \frac{\pi}{2} - \theta \right)$	$\cot \theta = \tan \left( \frac{\pi}{2} - \theta \right)$
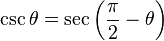	$\sec \theta = \csc \left( \frac{\pi}{2} - \theta \right)$	$\csc \theta = \sec \left( \frac{\pi}{2} - \theta \right)$

Paridad

Las funciones coseno y secante son pares, el resto son impares.

	Seno es impar $\sen\left(-\theta\right) = -\sen\left(\theta\right)$	csc es impar $\csc\left(-\theta\right) = -\csc\left(\theta\right)$
	cos es par $\cos\left(-\theta\right) = \cos\left(\theta\right)$	sec es par $\sec\left(-\theta\right) = \sec\left(\theta\right)$
	tan es impar $\tan\left(-\theta\right) = -\tan\left(\theta\right)$	cot es impar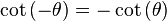 $\cot\left(-\theta\right) = -\cot\left(\theta\right)$

Periodicidad

Las funciones tangente y cotangente tienen una periodicidad de

\pi

, mientras que el resto tienen una periodicidad de

2\pi

	Seno: $2\pi$	csc: $2\pi$
	cos: $2\pi$	sec: $2\pi$
	tan: $\pi$	cot: $\pi$

Truco matemáticas: Trigonometría Fácil - Hexágono Trigonométrico

Nunca recuerdas las identidades trigonometricas?

Con este método con solo recordar el orden de 6 funciones trigonométricas prodrás tener a tu disposición 24 identidades trigonométricas. No es genial?

Bueno aqui el secreto,

Cada una de las letras es la representación de una función:

S: Seno
C: Coseno
T: Tangente
CT: Cotangente
SC: Secante
CSC: Cosecante

y el orden es de izquierda a derecha y de arriba hacia abajo,

Seno -----------Coseno.
Tangente ------Cotangente.
Secane- --------Cosecante.

Son tres relaciones:

Cada una de las funciones es igual al producto de las funciones que se encuentran a su lado, Ejemplo

T = S x SC.

Tangente = Seno x Secante.

Otro ejemplo:

S = T x C.

Seno = Tangente x Coseno.

Cada una de la funciones es igual a la función vecina entre la siguiente función en la misma dirección, Ejemplo

T = S / C.

Tangente = Seno / Coseno.

Otro ejempo:

T = SC / CSC.

Tangente = Secante / Cosecante.

Recuerda, siempre podrás relacionar 3 funciones que esten juntas. Si por ejemplo hay un ejercicio donde te den los valores de Seno y Coseno, al mirar el rectangulo te darás cuenta que estos datos son suficiente para deducir tanto la Tangente, como la Cotangente

Cada función es igual a 1 entre la función que tiene al frente, Ejemplo,

T = 1 / CT.

Tangente = 1 / Cotangente.

Otro ejemplo:

S = 1 / CSC.

Seno = 1 / Cosecante.

En la siguiente lista encontrarás todas las relaciones que puedes conseguir con el Hexágono Trigonométrico,

Seno
S = T x C	S = C / CT	S = T / SC	S = 1 / CSC
Coseno
C = S x CT	C = CT / CSC	C = S / T	C = 1 / CS
Tangente
T = SC x S	T = S / C	T = SC / CSC	T = 1 / CT
Cotangente
CT = C x CSC	CT = CSC / SC	CT = C / S	CT = 1 / T
Secante
SC = CSC x S	SC = T / S	SC = CSC / CT	SC = 1 / C
Cosecante
CSC = CT x SC	CSC = SC / T	CSC = CT / C	CSC = 1 / S

Ahora vamos con la telaraña trigonométrica, en ella se representan los lados de un triangulo simplificados de la siguiente forma,

O: Opuesto.
A: Adyacente.
H: Hipotenusa.

La relación es así,

Cada función es igual al lado que tiene arriba, sobre el que tiene abajo en la telaraña.

T = O / A.

Tangente = Opuesto / Adyacente.

Otro ejemplo,

S = O / H.

Seno = Opuesto / Hipotenusa.

Un ejemplo más...

CSC = H / O.

Cosecante = Hipotenusa / Opuesto.

Listado de relaciones con la telaraña trigonométrica,

S = O / H	C = A / H	T = O / A
CSC = H / O	SC = H /A	CT = A / O

AMIGOS PARA SIEMPRE

Páginas

martes, 30 de junio de 2015

Trigonometría

Funciones trigonométricas

Identidades pitagóricas

Identidades recíprocas

Productos

Cocientes

Identidades de la cofunción

Paridad

Periodicidad

Truco matemáticas: Trigonometría Fácil - Hexágono Trigonométrico

No hay comentarios:

Publicar un comentario

Datos personales

Archivo del blog