masa molar (símbolo M) de una sustancia dada es una propiedad física definida como su masa por unidad de cantidad de sustancia.1 Su unidad de medida en el SI es kilogramo por mol (kg/mol o kg·mol−1), sin embargo, por razones históricas, la masa molar es expresada casi siempre en gramos por mol (g/mol).
Las sustancias puras, sean estas elementos o compuestos, poseen una masa molar intensiva y característica. Por ejemplo, la masa molar aproximada del agua es: M (H2O) ≈ 18 g·mol−1.- ..................................................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=a2c3dcabf080347b8b2ac17d263bcff12e92a8fb&writer=rdf2latex&return_to=Masa+molar
Calculando la masa molar (peso molecular)
Para calcular la masa molar de un compuesto químico escribre su fórmula y dale clic en 'Calcular!'. En la fórmula química puede utilizar:
- Cualquier elemento químico
- Los grupos funcionales:D, Ph, Me, Et, Bu, AcAc, For, Ts, Tos, Bz, TMS, tBu, Bzl, Bn, Dmg
- paréntesis () o corchetes [].
- Nombres comunes del compuesto
Ejemplos de cálculos de la masa molar: NaCl, Ca(OH)2, K4[Fe(CN)6], CuSO4*5H2O, water, nitric acid, potassium permanganate, ethanol, fructose.
Calculando el peso molecular (masa molecular)
Para calcular el peso molecular de un compuesto quimico ingresa su formula, especifica su masa de isotopo despues de cada elemento en corchetes
Ejemplos de cálculos de peso molecular: C[14]O[16]2, S[34]O[16]2.
Ejemplos de cálculos de peso molecular: C[14]O[16]2, S[34]O[16]2.
Definiciones de masa molecular, peso molecular, masa molar y peso molar
- Masa molecular ( peso molecular ) es la masa de una molécula de una sustancia y se expresa en las unidades de masa atómica unificada (u). (1 u es igual a 1/12 de la masa de un átomo de carbono-12)
- Masa equivalente ( peso molar ) es la masa de un mol de una sustancia y se expresa en g / mol.
Los pesos de los átomos e isótopos son de NIST artículo .
href='/contact.php'> acerca de su experiencia con la calculadora del peso molecular.
href='/contact.php'> acerca de su experiencia con la calculadora del peso molecular.
magnitud molar parcial asociada a una variable extensiva, es la derivada parcial de dicha variable extensiva  con respecto a la variación del número de moles
con respecto a la variación del número de moles 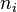 de una de las sustancias del sistema manteniendo la presión, la temperatura y el número de moles de las demás sustancias constantes. La propiedad molar parcial se representa por
de una de las sustancias del sistema manteniendo la presión, la temperatura y el número de moles de las demás sustancias constantes. La propiedad molar parcial se representa por  . La expresión es la siguiente:
. La expresión es la siguiente:
 con respecto a la variación del número de moles
con respecto a la variación del número de moles 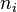 de una de las sustancias del sistema manteniendo la presión, la temperatura y el número de moles de las demás sustancias constantes. La propiedad molar parcial se representa por
de una de las sustancias del sistema manteniendo la presión, la temperatura y el número de moles de las demás sustancias constantes. La propiedad molar parcial se representa por  . La expresión es la siguiente:
. La expresión es la siguiente:![\bar{X}_i = \left [\frac {\partial X} {\partial n_i}\right ] _{P,T,n_{j \ne i}}](https://upload.wikimedia.org/math/9/c/b/9cb269ea103af76b1a5caeed5a1abb47.png)
Las magnitudes molares parciales se usan en mezclas para indicar la no aditividad de las propiedades extensivas de las mismas, es decir, la propiedad de la mezcla no es igual a la suma de la propiedad de los componentes puros por separado. Por ejemplo el volumen molar de una mezcla binaria no es la suma de los volúmenes molares de los componentes puros:

La propiedad molar parcial de una sustancia pura es igual a la magnitud molar correspondiente:
![\bar{X} = \left [\frac {\partial X} {\partial n}\right ] _{P,T} = X_m](https://upload.wikimedia.org/math/e/e/8/ee8fc378f19cab3aea9d2b5906246efb.png)
Matemáticamente las magnitudes molares parciales son funciones homogéneas de grado cero, es decir, no dependen de la cantidad de sustancia, por tanto variables intensivas.
Para el cálculo de la propiedad molar de una mezcla usamos la siguiente ecuación general a partir de las magnitudes molares parciales:
 (a P y T constantes)
(a P y T constantes)
Una propiedad molar parcial muy importante es la energía de Gibbs molar parcial o potencial químico.
Definición de MPM
Si se considera un sistema homogéneo abierto compuesto por varias sustancias, que no esté sometido a ningún campo, en el que se pueda despreciar las propiedades de su superficie; las magnitudes extensivas quedan determinadas por la cantidad de sustancia de sus componentes y dos de las tres variables de estado (p, T ó V). En un sistema de dos componentes, para una magnitud extensiva como el volumen (V), se halla dV, diferenciando con respecto a cada variable:
Donde n1 y n2 se refieren a las cantidades de sustancia de los componentes del sistema. Las siguientes expresiones se denominan magnitudes parciales molares, en este caso volumen molar parcial:
Sustituyendo estas expresiones en la anterior:
De donde se concluye que la magnitud parcial molar de un componente en una mezcla es la derivada parcial de la propiedad extensiva correspondiente con respecto a la cantidad de sustancia del componente en cuestión, manteniendo constante la temperatura, presión y cantidades de sustancia de los demás componentes.
Desde el punto de vista físico, las propiedades parciales molares, representan la variación de una propiedad extensiva del sistema debido a la adición, a temperatura y presión constantes, de un mol del componente sin que varíe apreciablemente la composición del sistema.
Para el mismo sistema anterior, a temperatura y presión constantes, se puede escribir:
Esta es la forma más simple de relacionar una función de estado con las magnitudes parciales molares correspondientes. Para integrar la expresión anterior, es necesario conocer las relaciones funcionales:
Como cada par de compuestos responden a una función característica, es necesario buscar una relación funcional general. Para el caso del volumen, que es una magnitud extensiva se tiene la expresión:
Según Helm cada uno de los términos del segundo miembro de la ecuación anterior representa un elemento de volumen, que es una magnitud extensiva –por serlo el volumen- y como cada uno de estos términos está dado por el producto de dos factores, uno de ellos debe ser intensivo y el otro extensivo. De este modo, como dT y dp son magnitudes intensivas –al serlo T y p-, las dos primeras derivadas parciales que los acompañan serán magnitudes extensivas, lo cual es cierto; ya que el volumen lo es. Como los diferenciales dni son magnitudes extensivas –al serlo la cantidad de sustancia-, se llega a la conclusión que las magnitudes parciales molares, que los acompañan en los términos correspondientes, serán intensivas, y representarán el volumen por mol.
De aquí se desprende que las funciones de estado extensivas son funciones homogéneas de primer grado de las cantidades de sustancia de los componentes del sistema: ni. Lo que significa que si todas las cantidades de sustancia se aumentan en una misma proporción, la función de estado se incrementará en esa misma proporción, permaneciendo la magnitud parcial molar –intensiva- constante.
Si se integra la expresión anterior, sin variar la composición del sistema la temperatura y la presión, se tiene:
Esta es la ecuación fundamental de las magnitudes parciales molares; representando la magnitud parcial molar, la contribución por mol que ese componente hace a la magnitud correspondienteen la solución considerada. Salvo en casos excepcionales –de soluciones denominadas ideales- la magnitud parcial molar difiere de la magnitud molar del componente puro. Así, por ejemplo, cuando se mezclan dos líquidos, el volumen de la mezcla resultante puede ser menor, igual o mayor que la suma de los volúmenes de los líquidos puros, que vendrían dados por los productos de sus cantidades de sustancia por sus volúmenes molares en estado puro.
De lo anterior se desprende que el volumen de un mol de sustancia pura es, en general, diferente de lo que sería el volumen molar de esa sustancia en la solución.
Al diferenciar la ecuación:
Anteriormente se había hallado para esta magnitud la ecuación:
Por lo que al restar ambas expresiones:
Teniendo en cuenta que las fracciones molares son:
Al combinarse las fracciones molares, cuya suma es la unidad:
Las que se sustituyen en (1):
Esta última expresión se conoce con el nombre de ecuación de Gibbs-Duhem y es de gran importancia en el tratamiento de las magnitudes parciales molares. Esta expresión indica que las variaciones de las magnitudes parciales molares con respecto a la composición del sistema no son independientes a una temperatura y presión constante.
La utilidad fundamental de esta ecuación es la obtención de las magnitudes parciales molares de uno de los componentes de la solución cuando se conocen las del otro.
Existen diversos métodos para determinar las magnitudes parciales molares, pero en la práctica, se emplean tres: el método analítico, el de la magnitud molar aparente y el de las intersecciones u ordenadas extremas.
Método analítico:
Una forma fácil de expresar la propiedad deseada para un rango amplio de composiciones, consiste en tomar una cantidad constante de uno de los componentes y agregar cantidades variables del otro componente, y medir el valor de la propiedad de interés para la solución o la variación de ésta.
Supongamos que se desea determinar los volúmenes parciales molares de los componentes de una solución binaria. Lo más práctico será formar soluciones de diferente molalidad y determinar sus densidades. Con ellas pueden obtenerse los volúmenes específicos correspondientes –volumen por unidad de masa- y con ellos pueden determinarse los volúmenes de las soluciones formadas por 100g de disolvente y la cantidad de sustancia de soluto que le corresponden a su molalidad.
Con esto se puede hacer un gráfico con los volúmenes de las diferentes soluciones como ordenada contra las respectivas molalidades como abscisas y entonces a la molalidad deseada se traza la tangente a la curva, siendo esta pendiente:
Como:
Resulta:
Para determinar  se recurre a la ecuación:
se recurre a la ecuación:
En este caso, el volumen V de la solución es numéricamente igual a la ordenada a la curva en ese punto y como los demás valores son conocidos se puede determinar  .
.
Otra forma sería ajustar los valores experimentales por mínimos cuadrados a una expresión de la forma:
A partir de esta ecuación se tiene:
Si el disolvente es agua:
Y por la ecuación fundamental, al sustituir se tiene:
El volumen de las soluciones de ácido sulfúrico en agua desde uno molal hasta seis molal responde bien a la ecuación empírica:
Donde m es la molalidad
Encuentre los volúmenes parciales molares del soluto y disolvente para una solución 4 molal.
Se tiene:
Mediante la ecuación:
Se tiene para este caso, ya que:
Sustituyendo:
Para m=4 se tiene:
El método de las magnitudes molares aparentes:
Método basado en la magnitud molar aparente:
La magnitud molar aparente φZ de una magnitud Z se define para el soluto de una solución binaria por:
Donde el subíndice 1 se refiere al disolvente y el 2 al soluto.
Del estudio de la expresión que le sirve de definición se infiere que el nombre es lógico, pues como la propiedad Z al formar la disolución no es estrictamente aditiva, entonces si al valor de la propiedad Z de la disolución se le sustrae el valor de esa propiedad para el total de disolvente (n1Z1), la falta de aditividad de esta propiedad se adjudica por entero al soluto, y al dividir por la cantidad de sustancia del soluto, la adjudicación se realiza por mol de soluto, lo cual es evidentemente aparente, pues una definición de esta naturaleza carece de simetría.
Despejando Z en la ecuación anterior:
De aquí que:
Y como:
Se tiene sustituyendo:
Por tanto:
Si la concentración de la disolución se expresa en función de la molalidad:
Si el disolvente es el agua: 
Por tanto, si los datos se expresan por una ecuación del tipo:
Basta derivar y sustituir en las ecuaciones anteriores.
Si solo se dispone de valores de φZ a sus respectivas molalidades se puede hacer una gráfica de φZ como ordenada contra m como abscisa y entonces, la pendiente de la curva en cualquier punto suministra:
Método de las intersecciones o de las ordenadas extremas:
También se conoce como el método de Bakhuis-Rooseboom y es muy utilizado, pues permite obtener las dos magnitudes parciales molares al unísono.
Representemos por z el valor medio de la propiedad Z de una solución binaria, es decir:
A temperatura y presión constante se deriva esta ecuación con respecto a n2, manteniendo n1 constante:
Esta ecuación puede transformarse de la siguiente manera. Como:
Al diferenciar esta ecuación a temperatura, presión y n1 constante se tiene:
Por tanto:
Si se llevan los datos a una gráfica donde los valores de z se tomen como ordenadas, y los de x1 como abscisas se puede obtener una curva como la de la siguiente figura:
|
|
Si se quieren determinar las magnitudes parciales molares cuando la composición de la solución sea la señalada por x1, se traza por el punto P la tangente AB.
En la figura se tiene:
Y como:
Se tiene:
De igual forma se demuestra que:
No hay comentarios:
Publicar un comentario