matemáticas - funciones

Una función especial es una función matemática particular, que por su importancia en el campo del análisis matemático, análisis funcional, la física y otras aplicaciones, posee nombres y designaciones más o menos establecidos.

No existe una definición general de las mismas, pero la lista de funciones matemáticas contiene funciones que son generalmente aceptadas como especiales. En particular, lasfunciones elementales son también consideradas funciones especiales.- .......................................:http://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=067a920b9c9e24ca349c44f71e949536d1bc84fc&writer=rdf2latex&return_to=Funci%C3%B3n+especial

FUNCIONES ESPECIALES Y TRANSFORMACIONES DE GRAFICAS

Función inversa:  Dada una función f(x), su inversa es otra función, designada por f^-1(x) de forma que se verifica: si f(a) = b, entonces f^-1(b) = a

Pasos a seguir para determinar la función inversa de una dada:

^_ Despejar la variable independiente x.

^_ Intercambiar la x por la y, y la y por la x.

La función así obtenida es la inversa de la función dada.

Las gráficas de dos funciones inversas son simétricas respecto de la bisectriz del 1.^er cuadrante y del 3.^er cuadrante.

 

Ejemplo: A es inversamente proporcional a B. Si A=3  cuando B=5, hallar a A cuando B=7

• 2 1/7

Función escalonada : Una función escalonada es aquella función definida a trozos que en cualquier intervalo finito [a, b] en que esté definida tiene un número finito de discontinuidades c₁ < c₂ < ... < c_n, y en cada intervalo ]

 

 

FUNCION VALOR ABSOLUTO:

La función de valor absoluto tiene por ecuación f(x) = |x|, y siempre representa distancias; por lo tanto, siempre será positiva o nula.

En esta condición, de ser siempre positiva o nula, su gráfica no se encontrará jamás debajo del eje x. Su gráfica va a estar siempre por encima de dicho eje o, a lo sumo, tocándolo.

Las funciones en valor absoluto siempre representan una distancia o intervalos (tramos o trozos) y se pueden resolver o calcular siguiendo los siguientes pasos:

1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces (los valores de x).

2. Se forman intervalos con las raíces (los valores de x) y se evalúa el signo de cada intervalo.

3. Definimos la función a intervalos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.

4. Representamos la función resultante.

 

FUNCION IDENTIDAD:

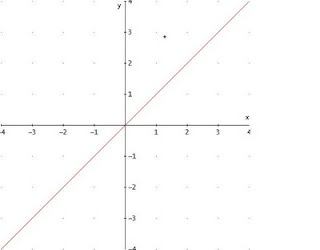
Es la función que es igual a la variable independiente.
f(x) = x
Su representación es una línea recta a 45º del eje x

 

 



 

FUNCION CONSTANTE:

Consideremos la función más sencilla, por ejemplo . La imagen de cualquier número es siempre 2. Si

hacemos una tabla de valores tendríamos:

x -2 -1 0 1 2

y 2 2 2 2 2

Por tanto si representamos todos esos valores, y más que podríamos calcular, todos están en el 2 y la

gráfica resulta una línea recta que corta al eje de ordenadas en el punto 2

En general una función constante es una función cuya fórmula es , donde k es un número

real. Su representación gráfica es una línea recta que corta al eje de ordenadas en el punto k.

Una función y(x) se llama implícita cuando está definida de la forma F(x, y) = 0 en lugar de la habitual.

Por ejemplo, puede probarse que la siguiente ecuación define una función implícita en cierta región de  entre las variables x e y:

Dada una función , implícita, si queremos calcular la derivada de y respecto de x: .

Si consideramos  es una función en términos de la variable independiente x y  es una función en términos de la variable dependiente y, dado que , entonces para obtener la derivada:

Función implícita

Una función f: X y es llamada función implícita, si la variable dependiente no se produce de forma explícita, en un lado de la ecuación, en términos de la variable independiente. En una función implícita, el valor de y puede ser obtenido resolviendo la ecuación en términos de x.

 La ecuación polinómica, conteniendo los términos tanto de x e y son muy difíciles de resolver. Si la ecuación no se resuelve para y, entonces y se llama una función implícita en términos de x, y tal ecuación se denomina función implícita. Una función implícita es generalmente de la forma,

Una función implícita también se conoce como un conjunto de nivel de cualquier función en términos de dos variables. Fuera de esas dos variables, una de ellas se puede determinar con la ayuda de otra variable. Pero no existe ninguna fórmula específica para determinar una variable en términos de otra variable.

Las funciones implícitas y las funciones explícitas están relacionadas entre sí con la ayuda del teorema de la función implícita. Según este teorema, si la función implícita satisface algunas de las condiciones, aunque levemente, sobre sus derivadas parciales entonces es posible resolver esta función para determinar el valor de y, al menos para un rango pequeño.

Si nos fijamos en la gráfica de una función implícita, nos encontraríamos con que su gráfica se superpone con la gráfica de la función f(x) = y, localmente.

Para tener una mejor comprensión, veamos el ejemplo dado a continuación,

Aquí x es una función implícita en términos de y, también y es una función implícita en términos de x. Para resolver la ecuación para la variable y, la ecuación se convertiría,

En la ecuación anterior, y es la función explícita de x. En el penúltimo ejemplo era fácil resolver la ecuación para y en términos de x, pero hay ocasiones en que la función dada es mucho más compleja y no se puede resolver fácilmente.

Una manera más simple y conveniente para resolver tal función es utilizar el método de diferenciación. Primeramente, diferencie la función dada que producirá la derivada dy/dx ó dx/dy, dependiendo de la variable que se considere implícita. Ahora resuelva para esta derivada.

Existen muchos más métodos para solucionar la función implícita, algunos de los cuales son iterativos. Aunque los métodos iterativos producen mejores resultados que los no iterativos en sus aproximaciones sucesivas, se utilizan en raras ocasiones debido a la complejidad que implica el uso de dichos métodos.

Al contrastar el número de ecuaciones (m) en el sistema con el número de variables (n), se puede adquirir información básica acerca de ese conjunto de nivel.

• Si n> m entonces existen infinitas soluciones del sistema de ecuaciones. Dicho sistema también se denomina indeterminado.

• Si n = m, entonces tenemos una única solución a nivel local para el sistema de ecuaciones y la ecuación se puede determinar con exactitud. Esto significa que si tenemos x como la solución de la ecuación entonces no existe ninguna otra solución para la ecuación cerca de x.

 • Si n - See more at: http://mitecnologico.com/igestion/Main/FuncionImplicita#sthash.N7CFJbxC.dpuf