Funciones aritméticas
En teoría de números, una función aritmética es una función real o compleja ƒ(n), definida sobre el conjunto de los números naturales, que "expresa alguna propiedad aritmética en función de n".
Una función aritmética a es
- completamente aditiva si a(mn) = a(m) + a(n) para todos los números naturales m y n;
- completamente multiplicativa si a(mn) = a(m)a(n) para todos los números naturales m y n;
Dos números enteros m y n son coprimos si su máximo común divisor es 1; es decir, si no existe un número primo que los divida a ambos.
Así, una función aritmética a es
- aditiva si a(mn) = a(m) + a(n) para todos los números naturales coprimos m y n;
- multiplicativa si a(mn) = a(m)a(n) para todos los números naturales coprimos m y n.
Función de la Aritmética
En teoría de números, una función aritmética es una función real o compleja ƒ(n), definida sobre el conjunto de los números naturales, que "expresa alguna propiedad aritmética en función de n".
Una función aritmética a es
- completamente aditiva si a(mn) = a(m) + a(n) para todos los números naturales m y n;
- completamente multiplicativa si a(mn) = a(m)a(n) para todos los números naturales m y n;
Dos números enteros m y n son coprimos si su máximo común divisor es 1; es decir, si no existe un número primo que los divida a ambos.
Así, una función aritmética a es
- aditiva si a(mn) = a(m) + a(n) para todos los números naturales coprimosm y n;
- multiplicativa si a(mn) = a(m)a(n) para todos los números naturales coprimos m y n.
Las funciones aritméticas trabajan con datos de tipo numérico NUMBER. Este tipo incluye los dígitos de 0 a 9, el punto decimal y el signo menos, si es necesario. Los literales numéricos no se encierran entre comillas. Ejemplo: -123.32.
Estas funciones trabajan con tres clases de números: valores simples, grupos de valores y listas de valores. Algunas modifican los valores sobre los que actúan; otras informan de algo sobre los valores. Podemos dividir las funciones aritméticas en tres grupos:
· Funciones de valores simples.
· Funciones de grupos de valores.
· Funciones de listas.
Al describir los formatos de las funciones utilizaremos los corchetes ([ ]) para indicar que lo que va encerrado es opcional.
¿Qué es una función aritmética?
Una función aritmética es una función  definida en los enteros positivos que de alguna manera refleja las propiedades aritméticas de
definida en los enteros positivos que de alguna manera refleja las propiedades aritméticas de 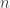 . Si bien esta definición es un tanto vaga, tradicionalmente sólo un pequeño número de funciones son consideradas aritméticas, de las cuales ya enumeramos algunas de las más importantes:
. Si bien esta definición es un tanto vaga, tradicionalmente sólo un pequeño número de funciones son consideradas aritméticas, de las cuales ya enumeramos algunas de las más importantes:
Ejemplo 1. La función número de divisores  .
.
Ejemplo 2. La función suma de divisores  . Es conveniente extender esta definición a sumas de potencias arbitrarias de divisores: para cada entero no negativo
. Es conveniente extender esta definición a sumas de potencias arbitrarias de divisores: para cada entero no negativo  definimos
definimos
Notemos que  y
y  ; no obstante, las notaciones
; no obstante, las notaciones  y
y 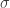 son tradicionales.
son tradicionales.
Ejemplo 3. La función  de Euler mencionada arriba.
de Euler mencionada arriba.
Entre la clase de funciones aritméticas, nos interesan particularmente las que poseen cierta propiedad distributiva respecto a la multiplicación.
Definición. Una función aritmética 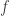 es multiplicativa si
es multiplicativa si  para cualesquiera enteros positivos coprimos
para cualesquiera enteros positivos coprimos  y
y 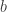 .
.
Una observación simple pero muy útil para la manipulación de funciones multiplicativas es que estas son completamente determinadas por los valores que toman en las potencias de primos. En efecto, por factorización única cualquier entero positivo 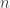 puede escribirse como
puede escribirse como  , por lo que si
, por lo que si 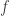 es multiplicativa entonces
es multiplicativa entonces
Las funciones multiplicativas surgen con frecuencia en la teoría de números; de hecho, el lector seguramente sospecha que ya vimos algunos ejemplos.
Ejemplo 1. La función  es multiplicativa. En efecto, si
es multiplicativa. En efecto, si 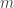 y
y 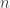 son coprimos, todo divisor de
son coprimos, todo divisor de  puede ser escrito en la forma
puede ser escrito en la forma  , donde
, donde  y
y  . Ya que hay
. Ya que hay  opciones para
opciones para  y
y  opciones para
opciones para  , se sigue que
, se sigue que  .
.
Ejemplo 2. La función 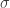 es multiplicativa. Usando la notación del párrafo anterior, lo que hay que verificar es
es multiplicativa. Usando la notación del párrafo anterior, lo que hay que verificar es
La expresión de la derecha no es otra cosa sino
pero ya dijimos en el ejemplo anterior que si  y
y  entonces
entonces  recorre los divisores de
recorre los divisores de  . Se sigue que esta suma es igual a
. Se sigue que esta suma es igual a  , que es justo lo que queríamos.
, que es justo lo que queríamos.
Ejemplo 3. La función  de Euler es multiplicativa. La prueba no es difícil, mas se desvía un poco de la discusión; el lector puede probar el resultado por su cuenta o bien consultar [1], Theorem 60, p. 53.
de Euler es multiplicativa. La prueba no es difícil, mas se desvía un poco de la discusión; el lector puede probar el resultado por su cuenta o bien consultar [1], Theorem 60, p. 53.
Una pregunta que surge naturalmente es cómo crear nuevas funciones multiplicativas a partir de otras. Una primera observación es la siguiente:
Proposición 1. El producto de dos funciones multiplicativas es una función multiplicativa.
Demostración. Evidente, pues si 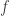 y
y 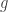 son multiplicativas, entonces
son multiplicativas, entonces
para cualesquiera  y
y 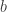 coprimos.
coprimos. 
Otra construcción importante utiliza la notación introducida al principio.
Proposición 2. Si 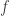 es una función multiplicativa, entonces
es una función multiplicativa, entonces
también es una función multiplicativa.
Demostración. Sean 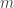 y
y 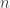 dos enteros positivos coprimos. Lo que debemos probar es
dos enteros positivos coprimos. Lo que debemos probar es  , o bien
, o bien
Para verificar esto procedemos tal y como en el Ejemplo 2. Expandiendo el producto de la derecha queda
donde  puesto que
puesto que  y
y  son coprimos (¿por qué?). Pero ya sabemos que si
son coprimos (¿por qué?). Pero ya sabemos que si  y
y  entonces
entonces  recorre todos los divisores de
recorre todos los divisores de  ; luego la suma de la derecha es igual a
; luego la suma de la derecha es igual a  , como queríamos.
, como queríamos. 
Ejemplo 4. La función  es multiplicativa, puesto que la función
es multiplicativa, puesto que la función  es multiplicativa. En particular, las funciones número de divisores
es multiplicativa. En particular, las funciones número de divisores  y suma de divisores
y suma de divisores  son multiplicativas.
son multiplicativas.
Nota. La proposición anterior es un caso particular de un teorema más general: es cierto que si 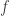 y
y 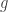 son funciones multiplicativas, entonces
son funciones multiplicativas, entonces
también es una función multiplicativa. La función  así obtenida suele denotarse por
así obtenida suele denotarse por  y se conoce como la convolución de Dirichlet de
y se conoce como la convolución de Dirichlet de 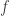 y
y 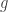 .
.
Ejercicio. Demuestre que la convolución de Dirichlet es asociativa, es decir: para cualesquiera funciones aritméticas 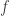 ,
, 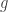 y
y  se cumple que
se cumple que
Solución al problema de Liouville
Ya estamos listos para enunciar y probar el acertijo planteado al principio de esta nota.
Teorema. Para todo entero positivo 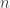 se cumple que
se cumple que
Demostración. Comenzamos notando que ambos lados de la ecuación definen funciones multiplicativas. Claramente 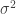 es multiplicativa, al ser el producto de dos funciones multiplicativas. Por la misma razón,
es multiplicativa, al ser el producto de dos funciones multiplicativas. Por la misma razón,  es multiplicativa, e invocando la Proposición 2 vemos que
es multiplicativa, e invocando la Proposición 2 vemos que  también es multiplicativa.
también es multiplicativa.
Por otra parte, los divisores de una potencia de un primo  son
son  , y los respectivos números de divisores de estos números son
, y los respectivos números de divisores de estos números son  . Luego
. Luego
y además
Pero para cualquier entero positivo 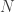 tenemos la famosa identidad
tenemos la famosa identidad
de donde es inmediato concluir que ambos lados de la ecuación inicial toman los mismos valores en potencias de primos, y ya que se trata de funciones multiplicativas, esto significa que deben ser iguales.

No hay comentarios:
Publicar un comentario