Aritmética

Funciones aritméticas

 función de Ackermann es una función matemática recursiva encontrada en 1926 por Wilhelm Ackermann, tiene un crecimiento extremadamente rápido, de interés para la ciencia computacional teórica y la teoría de la computabilidad. Hoy en día, hay una serie de funciones que son llamadas funciones Ackermann. Todas ellas tienen una forma similar a la ley original la función de Ackermann y también tienen un comportamiento de crecimiento similar. Esta función toma dos números naturales como argumentos y devuelve un único número natural. Como norma general se define como sigue:

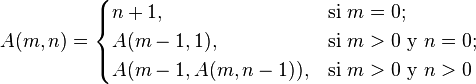 .- ....................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=8b6058dbfff0992eb20ce426038b091771a40438&writer=rdf2latex&return_to=Funci%C3%B3n+de+Ackermann

En 1928, Wilhelm Ackermann observó que A(x,y,z), la z-ésima exponenciación iterada de x con y como exponente, es una función recursiva que no es primitiva recursiva. En 1935, Rózsa Péter simplificó A(x,y,z) a una función de dos variables. En 1948, Raphael M. Robinson simplificó la condición inicial. Quedando una función doblemente recursiva de N² en N, definida recursivamente por las tres condiciones siguientes:

A[0, n_] := n + 1;

A[m_, 0] := A[m - 1, 1];

A[m_, n_] := A[m - 1, A[m, n - 1]];

Esta última versión es conocida hoy día como la función de Ackermann, el ejemplo más simple de una función total que es computable. O sea, que se puede implementar con ciclos de tipo "While". Pero que no es primitiva recursiva. Por tanto no se puede implementar sólo con ciclos de tipo "For".

Esto proporciona un contraejemplo a la creencia de principios del s. XX de que toda función computable era también primitiva recursiva. Por su definición inicial, la función de Ackermann crece más rápido que cualquier función exponencial, e incluso cualquier función exponencial mútiple.

De hecho, A[4,2] = 2²²²² − 3 = 2⁶⁵⁵³⁶ − 3 es un número natural con más de 19.000 dígitos en base 10.

Programación iterativa.

Para esta función, la programación iterativa es casi tan mala como la recursiva. El siguiente código escrito en Mathemática:

          Ackermann[m_Integer, n_Integer] :=
                 Module[{a = m, b = n, pila = {m, n}},
                 While[Length[pila] > 1,
                      pila = Drop[pila, -2];
                      Which[a == 0, If[Length[pila] >= 1, a = Last[pila]]; pila = Append[pila, ++b],
                            b == 0, pila = Join[pila, {--a, ++b}],
                            True, pila = Join[pila, {a - 1, a, --b}];
                      ]
                 ];
                 Return[b];] /; (m n) >= 0

Aunque correcto y funcional, no permite calcular A[4,2] en un tiempo razonable, en ningún ordenador actual. Sin embargo, el número 2⁶⁵⁵³⁶ − 3 se calcula en segundos.

Lo que enlentece el cálculo de la función de Ackermann, es tener que ir de uno en uno hacia atrás y hacia delante varias veces antes de alcanzar el número final, que acaba siendo enumerado muchas veces.

Mejorando la programación iterativa

Para mejorar un poco la programación iterativa, hay que demostrar algunos teoremas o propiedades sobre la función de Ackermann.

Demostraremos por inducción, que

Propiedad 1: A[1, n] = n + 2.

Veamos el primer caso de la inducción, por la segunda línea de la definición A[1, 0] = A[0, 1] y ahora por la primera A[0, 1] = 1 + 1 = 2 = 0 + 2 que es lo queríamos demostrar.

Ahora, sin escribir el nombre de la función, tenemos

[1, n ] = (por la tercera línea de la definición) = [0, 1, n - 1] = (por inducción) = [0, n - 1 +2] = [0, n + 1] = (por la primera línea de la definición) = n + 1 + 1 = n + 2

como queríamos demostrar.

Ahora, podemos demostrar por inducción, que

Propiedad 2: A[2, n] = 2 n + 3.

Veamos el primer caso de la inducción. Sin escribir el nombre de la función, tenemos

[2, 0] = (por la segunda línea de la definición) = [1, 1] = (por el caso anterior) = 1 + 2 = 3 = 2*0 + 3

como queríamos. Ahora por hipótesis de inducción:

[2, n ] = (por la tercera línea de la definición) = [1, 2, n - 1] = (por inducción) = [1, 2(n - 1) +3] = [1, 2 n + 1] = (por caso anterior) =
= 2 n + 1 + 2 = 2 n + 3

como queríamos demostrar.

Ahora, podemos demostrar por inducción, que

Propiedad 3: A[3, n] = 2^{n + 3} - 3.

Veamos el primer caso de la inducción. Sin escribir el nombre de la función, tenemos

[3, 0] = (por la segunda línea de la definición) = [2, 1] = (por el caso anterior) = 2*1 + 3 = 5 = 2^{0 + 3} - 3

como queríamos. Ahora por hipótesis de inducción:

[3, n ] = (por la tercera línea de la definición) = [2, 3, n - 1] = (por inducción) = [2, 2^{n + 2} - 3] = (por caso anterior) = 2 (2^{n + 2} - 3) + 3 =
= 2^{n + 3} - 3

como queríamos demostrar.

Ahora, podemos demostrar por inducción, que

Propiedad 4: A[4, n] = 2^22...2 − 3 . Donde el primer sumando es una potencia anidada de n + 3 niveles.

Veamos el primer caso de la inducción. Sin escribir el nombre de la función, tenemos

[4, 0] = (por la segunda línea de la definición) = [3, 1] = (por el caso anterior) = 2^{1 + 3} - 3 = 2²² - 3 = 13

como queríamos. Ahora por hipótesis de inducción:

[4, n ] = (por la tercera línea de la definición) = [3, 4, n - 1] = (por inducción) = [3, 2^22...2 − 3] = (por caso anterior) = 2^22...22 − 3

obtenemos un nivel más en el primer sumando, como queríamos demostrar.

Estas 4 funciones son fáciles de implementar en cualquier lenguaje o paquete con aritmética de precisión múltiple y suponen una mejora sustancial para estos niveles. Sin embargo, la velocidad de crecimiento de A[4,n] es tan grande que hace imposible y sin sentido calcularla para valores grandes de n.

FUNCION DE ACKERMAN EN C++

En teoría de la computación, la función de Ackermann es una función recursiva que toma dos números naturales como argumentos y devuelve un único número natural. Como norma general se define como sigue:

Implementación

123456789101112131415161718192021222324252627282930313233343536

#include <iostream> #include <cstdlib>   using namespace std;   int Ackerman(int m, int n) { if(m==0) return n+1; else { if(n==0) return Ackerman(m-1, 1); else return Ackerman(m-1, Ackerman(m, n-1)); } } int main() { int m, n, num ;   cout<<"\n FUNCION DE ACKERMAN \n\n";   cout<<"Ingrese : "; cin>> m ; cout<<"Ingrese : "; cin>> n ; num = Ackerman(m,n); cout<<"\nEl numero es: "<< num <   system("pause"); return 0; }