el campo de la aritmética, la función μ (« mu » o « my ») de Möbius se define así:
| Para todo número natural n se considera su descomposición en factores primos : |
- Si n contiene un factor cuadrado, es decir si una de las potencias ri es superior o igual a dos, entonces se decide que μ(n) = 0.
- Si no es el caso, n es «libre de cuadrado», y se define así la función:
- Si n tiene un número par de factores primos, entonces μ(n) = 1
- Si n tiene un número impar de factores primos, entonces μ(n) = -1
| En ambos casos, n se escribe | (todos los ri son iguales a 1 ), y μ(n) = (-1)k. |
Ejemplos:
- μ(1) = 1 porque 1 es un producto de cero factor primo (un producto vacío), y cero es par.
- μ(18) = 0 porque 18 = 2×32 contiene el factor cuadrado 9.
- μ(32) = 0 porque 32 = 25 contiene los cuadrados 4 = 22 y también 16 = 24.
- μ(30) = -1 pues 30 = 2×3×5 es producto de tres (impar) primos distintos.
- μ(77)= 1 pues 77 = 7×11 es un producto de dos (par) primos distintos.
Una propiedad: Si m y n son coprimos, entonces μ(m·n) = μ(m)·μ(n). Es la multiplicatividad condicional.
Prueba: Si m o n contiene un cuadrado, entonces el producto m·n también, y los dos miembros de la igualdad son iguales a cero. Si no, sea k y k' los números de factores de my n. Entonces m·n tiene k + k' factores primos, todos distintos porque m y n son coprimos, y la igualdad se escribe sencillamente (-1) k + k' = (-1) k · (-1) k'.
II Interés
La función de Möbius fue inventada para resolver sistemas particulares de ecuaciones. Para entenderlo, hay que introducir el producto de convolución entre dos sucesiones (o funciones sobre los enteros naturales): si f y g son sucesiones, se define su producto f*g así:
Este producto es conmutativo, asociativo, y su neutro es la sucesión ε = (1, 0, 0, 0, 0 ...) es decir: ε(0) = 1 y ε(n) = 0 para todo n > 0.
| Llamemos 1 la sucesión constante de valor 1. Entonces: |
Supongamos ahora que tengamos que resolver el sistema siguiente, con una infinidad de líneas y de incógnitas – las f(n) – (las g(n) son conocidas)
En términos de convolución, este sistema se escribe f*1 = g.
Para hallar f, hay que multiplicar ambos miembros de la ecuación por el inverso de la sucesión 1, y este es justamente la sucesión μ de Möbius (prueba más adelante).
Luego (f*1)*μ = g*μ que equivale a f*(1*μ) = g*μ (asociatividad), es decir f*ε = g*μ y finalmente f = g*μ.
Para hallar f, hay que multiplicar ambos miembros de la ecuación por el inverso de la sucesión 1, y este es justamente la sucesión μ de Möbius (prueba más adelante).
Luego (f*1)*μ = g*μ que equivale a f*(1*μ) = g*μ (asociatividad), es decir f*ε = g*μ y finalmente f = g*μ.
En síntesis:
En términos de sistemas: Para todo n entero natural no nulo,
Esta propiedad se llama «fórmula de inversión de Möbius» .
Falta demostrar que las funciones μ y 1 son inversas la una de la otra, es decir: μ * 1 = ε, concretamente:
| Para n = 1 , | y si n > 1, |
Lo primero es obvio porque la suma vale μ (1) = 1.
Lo segundo se muestra por etapas:
- Si n = p es primo entonces la suma es μ(1) + μ(p) = 1 – 1 = 0.
- Si n = pr (r>1), la suma es μ(1) + μ(p) + μ(p2) + ... + μ( pr) = 1 – 1 + 0 + ... + 0 = 0.
- Si n = a·b, con a y b coprimos, los divisores de a·b son de la forma d1·d2, con d1 y 2 coprimos. Como hipótesis de inducción admitimos el resultado para a y b (ambos superiores a 1). Luego:
La «inversión» del sistema anterior es, aplicando la fórmula:
Claro, se puede resolver el sistema "paso a paso" y se hallará la misma solución.
| Aplicada a la función fi de Euler, la inversión da como expresión: |
transformada de Möbius, llamada así en honor a August Ferdinand Möbius es una transformación defunciones aritméticas. Si f es una función definida sobre los números enteros positivos, Tf viene dada por
donde μ es la función de Möbius clásica.1 En un lenguaje más común y extendido por razones históricas, la función Tf se llama inversa de Möbius de f.2 (La notación d | n significa que d es un divisor de n).
La transformación toma funciones aritméticas, o sea, funciones f: N → C y devuelve funciones aritméticas. Sobre funciones generadas mediante series de Dirichlet, se corresponde a una división por la función zeta de Riemann.
La transformada inversa T-1f viene dada por
|






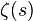 es la
es la
No hay comentarios:
Publicar un comentario