AMIGOS PARA SIEMPRE: Aritmética

Funciones aritméticas

serie de Bell es una serie de potencias formal utilizada para estudiar la propiedades de funciones aritméticas. Las series de Bell fueron introducidas y desarrolladas por Eric Temple Bell.

Dada una función aritmética

f

y un número primo

p

, se define la serie de potencias formal

f_p(x)

, llamada serie de Bell de

f

módulo

p

como:

f_p(x)=\sum_{n=0}^\infty f(p^n)x^n.

Se puede demostrar que dos funciones multiplicativas son idénticas si todas sus series de Bell son iguales; esto a veces se llamateorema de unicidad. Dadas las funciones mutiplicativas

f

g

, se tiene que

f=g

si y sólo si:

f_p(x)=g_p(x)

para todos los primos

p

Dos series pueden ser multiplicadas (a veces llamado como teorema de multiplicación): Para dos funciones aritméticas cualesquiera

f

g

, sea

h=f*g

su convolución de Dirichlet. Entonces, para cada primo

p

, se tiene que:

h_p(x)=f_p(x) g_p(x).\,

En particular, esto convierte en trivial el encontrar la serie de Bell de una inversa de Dirichlet.

f

es completamente multiplicativa, entonces:

f_p(x)=\frac{1}{1-f(p)x}.

A continuación se muestran las series de Bell de funciones aritmética muy conocidas.

La función de Möbius $\mu$ tiene $\mu_p(x)=1-x.$
Función φ de Euler $\varphi$ tiene $\varphi_p(x)=\frac{1-x}{1-px}.$
La identidad multiplicativa de la convolución de Dirichlet 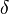$\delta$ tiene $\delta_p(x)=1.$
La función de Liouville $\lambda$ tiene $\lambda_p(x)=\frac{1}{1+x}.$
La función potencia Id_k tiene $(\textrm{Id}_k)_p(x)=\frac{1}{1-p^kx}.$ Aquí, Id_k es la función completamente multiplicativa $\operatorname{Id}_k(n)=n^k$ .
La función divisor $\sigma_k$ tiene $(\sigma_k)_p(x)=\frac{1}{1-(1+p^k) x+p^kx^2}.$

símbolo de Jacobi, denotado como

\left ( \frac{m}{n} \right)

, es una función aritmética que toma dos argumentos y devuelve un valor enterocomprendido en el intervalo

[-1, 1]

. En esencia se puede considerar como una generalización del símbolo de Legendre para valores impares de

n

que no necesariamente han de ser primos. Debe su nombre al matemático Carl Gustav Jakob Jacobi.

Sea m un número entero y n un número natural impar, se denomina símbolo de Jacobi a la expresión:

\left ( \frac{m}{n} \right) = \prod_{i=1}^{k}\left ( \frac{m}{p_i} \right)^{a_i}

donde para todo i, p_i es primo y a_i es un número natural, siendo

n = \prod_{i=1}^{k}p_i^{a_i}

y denotando mediante

\left ( \frac{m}{p_i} \right)

el símbolo de Legendre.

Obviamente, cuando n es un número primo, el correspondiente símbolo de Jacobi se reduce al de Legendre.

El símbolo de Jacobi satisface las mismas reglas que aquél al que generaliza, además de algunas adicionales:

i) Si

n|m

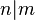entonces

\left ( \frac{m}{n} \right)=0

ii) Un caso especial de esto último es que

\left ( \frac{m}{m} \right)=0

iii) Si

m

n

son números impares primos relativos entre sí, y

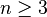n \geq 3

se cumple la siguiente relación:

\left ( \frac{m}{n} \right)\left ( \frac{n}{m} \right)=(-1)^{(m-1)(n-1)/4}

símbolo de Legendre,

\left ( \frac{a}{p} \right)

, es una función multiplicativa utilizada en teoría de números que toma como argumentos un entero

a

y un primo

p

y devuelve uno de los valores 1, -1, ó 0 dependiendo de si

a

es o no residuo cuadrático módulo

p

, es decir de si la congruencia

x^2 \equiv a \pmod p

tiene o no solución.

Dado un número a y un primo p, se define el s:

\left ( \frac{a}{p} \right ) = \begin{cases} 0 & \mbox{si } p \mbox{ divide a }a \\ 1 & \mbox{si } a\mbox{ es residuo cuadrático módulo } p \\ -1 & \mbox{si } a\mbox{ no es residuo cuadrático módulo } p \\ \end{cases}

x = 2 \Rightarrow 2^2 \equiv 1 \pmod 3 \Rightarrow \left ( \frac{1}{3} \right)= 1

Para algunos valores concretos de

a

, el símbolo de Legendre aún puede simplificarse más:

\left ( \frac{-1}{p} \right) = (-1)^{(p-1)/2}

\left ( \frac{2}{p} \right) = (-1)^{(p^2-1)/8}

El símbolo de Legendre satisface algunas propiedades interesantes:

\left ( \frac{q}{p} \right ) = \left ( \frac{p}{q} \right ) (-1)^{[(p-1)/2][(q-1)/2]}

ii)

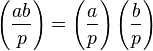\left ( \frac{ab}{p} \right) =\left ( \frac{a}{p} \right) \left ( \frac{b}{p} \right)

símbolo de Kronecker, escrito como

\left(\frac an\right)

o (a|n), es una generalización del símbolo de Jacobi para todos losnúmeros enteros n. Fue introducido por Leopold Kronecker.

Sea n un número entero distinto de cero, con una factorización en números primos

u \cdot {p_1}^{e_1} \cdots {p_k}^{e_k},

donde u es una unidad (i.e., u es 1 o −1), y los p_i son números primos. Sea a un entero. El símbolo de Kronecker (a|n) se define como:

\left(\frac{a}{n}\right) = \left(\frac{a}{u}\right) \prod_{i=1}^k \left(\frac{a}{p_i}\right)^{e_i}.

Para números impares p_i, el (a|p_i) se reduce simplemente al símbolo de Legendre. Queda el caso en el que p_i = 2. Se define (a|2) por

\left(\frac{a}{2}\right) = \begin{cases} 0 & \mbox{si }a\mbox{ es par,} \\ 1 & \mbox{si } a \equiv \pm1 \pmod{8}, \\ -1 & \mbox{si } a \equiv \pm3 \pmod{8}. \end{cases}

Puesto que extiende el símbolo de Jacobi, la cantidad (a|u) es simplemente 1 cuando u = 1. Cuando u = −1, se define éste por

\left(\frac{a}{-1}\right) = \begin{cases} -1 & \mbox{si }a < 0, \\ 1 & \mbox{si } a \ge 0. \end{cases}

Finalmente, tenemos que

\left(\frac a0\right)=\begin{cases}1&\text{si }a=\pm1,\\0&\text{de otra manera.}\end{cases}

Estas extensiones son suficientes para definir el símbolo de Kronecker para todos los valores enteros n.

sucesión alícuota es una sucesión recursiva en la que cada término es la suma de los divisores propios del término anterior. La sucesión alícuota que comienza con el entero positivo k puede ser definida formalmente mediante la función divisor σ₁ de la siguiente manera:¹

s₀ = k

s_n = σ₁(s_n−1) − s_n−1.

Por ejemplo, la sucesión alícuota de 10 es 10, 8, 7, 1, 0 porque:

σ₁(10) − 10 = 5 + 2 + 1 = 8

σ₁(8) − 8 = 4 + 2 + 1 = 7

σ₁(7) − 7 = 1

σ₁(1) − 1 = 0

Muchas sucesiones alícuotas terminan en cero (sucesión A080907 en OEIS); todas las sucesiones de ese tipo necesariamente terminan con un número primo seguido por 1 (ya que el único divisor propio de un primo es 1), seguido por 0 (ya que 1 no tiene divisores propios). Hay varias maneras en las cuales una sucesión alícuota puede no terminar:

Un número perfecto (A000396) tiene una sucesión alícuota periódica infinita de período 1. La sucesión alícuota de 6, por ejemplo, es 6, 6, 6, 6, ....
Un número amigable (A063990) tiene una sucesión alícuota infinita de período 2. Por ejemplo, la sucesión alícuota de 220 es 220, 284, 220, 284, ....
Un número sociable tiene una sucesión alícuota infinita de período mayor o igual a 3 (a veces, el término número sociable se aplica también a los números amigables). Por ejemplo, la sucesión alícuota de 1264460 es 1264460, 1547860, 1727636, 1305184, 1264460, ....
Algunos números tienen una sucesión alícuota que termina en una sucesión periódica, pero el número inicial no es perfecto, amigable, ni sociable. Como ejemplo, la sucesión alícuota de 95 es 95, 25, 6, 6, 6, 6, .... Números como 95 que no son perfectos, pero tienen una sucesión alícuota periódica de período 1 son llamados números aspirantes (A063769).

Una importante conjetura enunciada por Catalan respecto a las sucesiones alícuotas es que cada sucesión alícuota termina en una de las tres formas descritas arriba — con un número primo, un número perfecto, o un conjunto de números amigables o sociables.² La alternativa sería que exista un número cuya sucesión alícuota fuera infinita, pero aperiódica. Hay varios números cuyas sucesiones alícuotas no han sido totalmente determinadas (año 2006), por lo que podrían existir tales números. Los primeros cinco números candidato son llamados los cinco de Lehmer: 276, 552, 564, 660, and 966.³

Hasta la fecha (agosto de 2009), hay 906 enteros positivos menores que 100000 cuyas sucesiones alícuotas no han sido completamente determinadas, y 9393 si se incluyen todos los enteros positivos menores que 1000000.

La función φ de Euler (también llamada función indicatriz de Euler) es unafunción importante en teoría de números. Si n es un número entero positivo, entonces φ(n) se define como el número de enteros positivos menores o iguales a ny coprimos con n, es decir, formalmente se puede definir como:

$\varphi(m) = |\{n \in \mathbb{N} | n \leq m \and \mathrm{mcd}(m, n) = 1 \}|$

donde |·| significa la cantidad de números que cumplen la condición.

La función φ es importante principalmente porque proporciona el tamaño del grupo multiplicativo de enteros módulo n. Más precisamente,

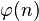\varphi(n)

es el orden del grupo de unidades del anillo

\mathbb{Z}/n\mathbb{Z}

. En efecto, junto con el teorema de Lagrange de los posibles tamaños de subgrupos de un grupo, proporciona una demostración delteorema de Euler que dice que

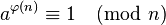a^{\varphi(n)}\equiv 1 \pmod{n}

para todo a coprimo conn. La función φ juega también un papel clave en la definición del sistema de cifrado RSA.- ............................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=274899b6af5f07cb12304f925e5fbba2e53bfc77&writer=rdf2latex&return_to=Funci%C3%B3n+%CF%86+de+Euler

Unidades en Z_m

Denotamos por U_m al conjunto de elementos invertibles de Z_m.

U_m es llamado por algunos autores como el conjunto reducido de residuos módulo m.

Cuando m es primo, todos los enteros {1,...,m-1} son invertibles en Z_m, por lo tanto el cardinal |U_m | = m-1

En Z_m se cumple que:

Si [a], [b] ∈ U_m entonces [a].[b] ∈ U_m y también [a]^-1 ∈ U_m
Si [a] ∈ U_m entonces [a].U_m = U_m

La función φ de Euler

Se define la función φ de Euler con la función φ: N ⇒ N que a cada n le hace corresponder el número de enteros x (1<x<n), que son primos relativos con n, esto es, cuyo mcd(x,n)=1.

Siempre se cumple que φ(p)= |U_p|

Así tenemos que φ(1)=1, φ(2)=1, φ(3)=2, φ(4)=2; φ(5)=4, φ(6)=2, φ(7)=6, φ(8)=4, φ(9)=6,...

Y cuando p es primo, φ(p) = p-1. Ejemplo: φ(17)=16.

Teoremas de Euler y de Fermat

El teorema de Euler

Si [a] ∈ U_m entonces [a]^φ(m) = [1] en Z_m.

Por tanto, si un b ∈ Z verifica que mcd(m,b)=1 entonces b^φ(m) ≡ 1 (mod m)

El Pequeño teorema de Fermat

Si p es primo y p no divide a a entonces:

a^p-1 ≡ 1 (mod p)

Números pseudoprimos

Si se cumpliese la implicación contraria en el teorema de Fermat (que si se cumpliere que a^p-1 ≡ 1 (mod p) con a no múltiplo de p, entonces podría asegurarse que p es primo), tendríamos una forma inmediata de comprobar si un número dado es primo. Desgraciadamente, hay ciertos números compuestos que satisfacen el teorema de Fermat. A esta clase de números compuestos se la denomina números pseudoprimos.

Un ejemplo de número pseudoprimo es el 341=11.31, ya que se cumple que 2³⁴⁰ ≡ 1(mod 341). Para verificar el resultado de esa potencia, puede usarse el applet de exponenciación modular en esta nueva ventana

Test de primalidad y generación de números primos

Tests de primalidad

Para números muy grandes, como los usados en sistemas criptográficos como el RSA, que llegan a tener tamaños de entre 512 y 2048 bits, no es viable en un tiempo razonable el tratar de factorizar un número para saber si es o no primo. Pero existen métodos probabilísticos que nos pueden decir con un alto grado de certeza si un número es primo o compuesto. A estos métodos se les llama tests de primalidad.

El mismo teorema de Fermat nos proporciona un método probabilístico para ver si un número es primo o no. Si un número p satisface el pequeño teorema de Fermat es probable que sea primo, aunque como ya se ha visto no podemos estar seguros de ello, ya que hay números compuestos (los pseudoprimos) que igualmente pueden pasar ese test.

A lo largo del tiempo se han inventado tests de primalidad más eficientes que el teorema de Fermat. Todos ellos tienen en común que dan un resultado probable sobre la primalidad de p con una probabilidad de error determinada, y mediante iteraciones sucesivas del método podemos obtener mayores grados de certeza sobre el resultado. Cuanto mayor grado de certeza queramos tener, más iteraciones del método habrá que hacer y más tiempo computacional tardará en terminar el test.

Así, si usamos un test de primalidad, como el método de Lehmann o algún otro, que nos indica si un número p es primo con una probabilidad de error menor o igual que 0.5 en el peor caso, si repetimos el método para p (con distintos parámetros, claro) n veces seguidas, al final la probabilidad de error será de 1 contra 2ⁿ.

Generación de números primos

A efectos prácticos, un algoritmo que se suele emplear en las aplicaciones (por ejemplo, como Matlab o Maple) para generar aleatoriamente un número primo p con n bits es el siguiente:

Generar un número aleatorio p de n bits.
Poner a uno el bit más significativo (así garantizamos que el número es de n bits) y el menos significativo (debe ser impar para poder ser primo)
Intentar dividir p por una tabla de primos precalculados (usualmente aquellos que sean menores que 2000). Esto elimina gran cantidad de números no primos de una forma muy rápida. Baste decir a título informativo que más del 99.8 % de los números impares no primos es divisible por algún número primo menor que 2000.
Ejecutar tests de primalidad sobre p para ver si es primo hasta el grado de certeza deseado
Si el test falla, incrementar p en dos unidades y volver al paso 3.

AMIGOS PARA SIEMPRE

Páginas

martes, 23 de junio de 2015

Aritmética

Funciones aritméticas