Constantes físicas
constante Verdet mide la fuerza del efecto Faraday para un material particular. Su valor depende no solo el material sino de la longitud de la onda electromagnética. La constante de Verdet recibe el nombre del físico francés Émile Marcel Verdet (1824-1866). En el Sistema Internacional de Unidades, la unidad es rad m-1 T-1.
El ángulo α por el cual la polarización a través de un material con el espesor d girar por el efecto Faraday es proporcional a la constante de Verdet V:1
Donde B es la densidad de flujo magnético en el material, paralelo a la dirección de propagación de la onda electromagnética.
El valor de la constante de Verdet se puede calcular a partir de la dispersión  del material considerado:2
del material considerado:2
 del material considerado:2
del material considerado:2
Para la mayoría de los materiales la constante de Verdet es extremadamente pequeña. Es más fuerte en las sustancias que contienen iones paramagnéticos tales como el terbio. Existen constantes de Verdet altas en vidrios densos dopados con terbio o en cristales degranate de galio-terbio (TGG). Este material tiene excelente transparencia y es muy resistente a los daños con luz láser.
El efecto Faraday es cromático (es decir, que depende de la longitud de onda) y por lo tanto la constante de Verdet es una función con una dependencia bastante fuerte de la longitud de onda. A 632.8 nm , la constante de Verdet para TGG se informó ser -134 rad T-1·m-1, mientras que a 1064 nm corresponde a -40 rad T-1·m-1. Este comportamiento indica que los dispositivos fabricados con un cierto grado de rotación en una longitud de onda, producirán una rotación mucho menor en longitudes de onda mayores. Muchos rotadores de Faraday y aisladores son ajustables mediante la variación del grado en que se inserta la varilla activa TGG en el campo magnético del dispositivo. De esta manera, el dispositivo puede ser sintonizado para su uso con una variedad de láseres dentro del rango de diseño del dispositivo. En dispositivos de banda ancha de emisión (por ejemplo, las fuentes de pulsos láseres ultra-cortos sintonizables y los láseres vibrónicos ) no verá la misma rotación en toda la banda de longitudes de onda.
constante de Coulomb (denotada  o
o 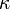 ) es una constante de proporcionalidad en las ecuaciones que relacionan variables eléctricas y es exactamente igual a
) es una constante de proporcionalidad en las ecuaciones que relacionan variables eléctricas y es exactamente igual a  = 8.9875517873681764×109 N·m2/C2 (m/F). Recibe el nombre del físico francés Charles-Augustin de Coulomb (1736–1806).
= 8.9875517873681764×109 N·m2/C2 (m/F). Recibe el nombre del físico francés Charles-Augustin de Coulomb (1736–1806).
 o
o 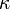 ) es una constante de proporcionalidad en las ecuaciones que relacionan variables eléctricas y es exactamente igual a
) es una constante de proporcionalidad en las ecuaciones que relacionan variables eléctricas y es exactamente igual a  = 8.9875517873681764×109 N·m2/C2 (m/F). Recibe el nombre del físico francés Charles-Augustin de Coulomb (1736–1806).
= 8.9875517873681764×109 N·m2/C2 (m/F). Recibe el nombre del físico francés Charles-Augustin de Coulomb (1736–1806).
A su vez la constante  donde
donde 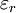 es la permitividad relativa,
es la permitividad relativa,  , y
, y 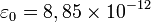 F/m es la permitividad del medio en el vacío.
F/m es la permitividad del medio en el vacío.
 donde
donde 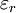 es la permitividad relativa,
es la permitividad relativa,  , y
, y 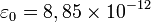 F/m es la permitividad del medio en el vacío.
F/m es la permitividad del medio en el vacío.
Cuando el medio que rodea a las cargas no es el vacío hay que tener en cuenta la constante dieléctrica y la permitividad del material.
Fuerza Eléctrica
En 1785, Charles Augustin de Coulomb (1736-1806), físico e ingeniero francés que también enunció las leyes sobre el rozamiento, presentó en la Academia de Ciencias de París, una memoria en la que se recogían sus experimentos realizados sobre cuerpos cargados, y cuyas conclusiones se pueden resumir en los siguientes puntos:
- Los cuerpos cargados sufren una fuerza de atracción o repulsión al aproximarse.
- El valor de dicha fuerza es proporcional al producto del valor de sus cargas.
- La fuerza es de atracción si las cargas son de signo opuesto y de repulsión si son del mismo signo.
- La fuerza es inversamente proporcional al cuadrado de la distancia que los separa.
Estas conclusiones constituyen lo que se conoce hoy en día como la ley de Coulomb.
La fuerza eléctrica con la que se atraen o repelen dos cargas puntuales en reposo es directamente proporcional al producto de las mismas, inversamente proporcional al cuadrado de la distancia que las separa y actúa en la dirección de la recta que las une.
donde:
- F es la fuerza eléctrica de atracción o repulsión. En el S.I. se mide en Newtons (N).
- Q y q son lo valores de las dos cargas puntuales. En el S.I. se miden en Culombios (C).
- r es el valor de la distancia que las separa. En el S.I. se mide en metros (m).
- K es una constante de proporcionalidad llamada constante de la ley de Coulomb. No se trata de una constante universal y depende del medio en el que se encuentren las cargas. En concreto para el vacío k es aproximadamente 9·109 N·m2/C2 utilizando unidades en el S.I.
Si te fijas bien, te darás cuenta que si incluyes el signo en los valores de las cargas, el valor de la fuerza eléctrica en esta expresión puede venir acompañada de un signo. Este signo será:
- positivo. cuando la fuerza sea de repulsión (las cargas se repelen). ( + · + = + o - · - = + )
- negativo. cuando la fuerza sea de atracción (las cargas se atraen). ( + · - = - o - · + = - )
Por tanto, si te indican que dos cargas se atraen con una fuerza de 5 N, no olvides que en realidad la fuerza es -5 N, porque las cargas se atraen.
Expresión vectorial de la fuerza eléctrica
La fuerza eléctrica descrita en la ley de Coulomb no deja de ser una fuerza y como tal, se trata de una magnitud vectorial que en el Sistema Internacional de Unidades se mide en Newtons (N). Su expresión en forma vectorial es la siguiente:
donde el nuevo valor u⃗ r es un vector unitario en la dirección que une ambas cargas. Observa que si llamamos r⃗ al vector que va desde la carga que ejerce la fuerza hacia la que la sufre, u⃗ r es un vector que nos indica la dirección de r⃗
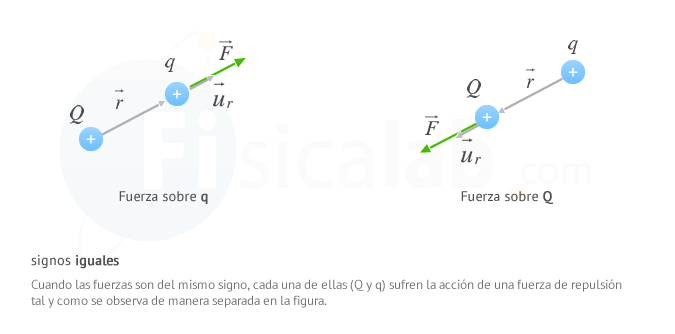
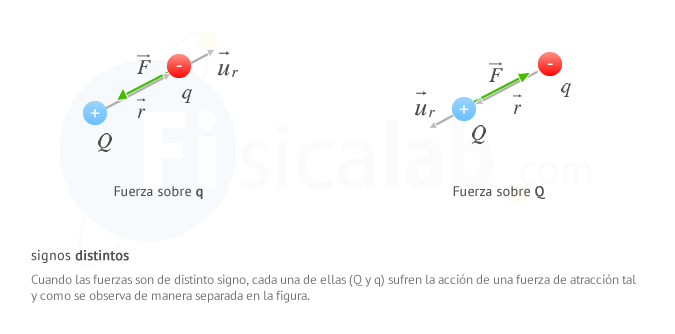
Date cuenta que la fuerza electrica siempre tiene la misma dirección que el vector unitario u⃗ r y el mismo sentido si tienen el mismo signo y sentido opuesto si tienen signo distinto.
No olvides que debes incluir el signo de las cargas cuando utilices la expresión de la ley de Coulomb.
Constante dieléctrica o permitividad del medio
Dado que la constante la ley de Coulomb K depende del medio, esta suele expresarse en términos de otra constante denominada constante dieléctrica o permitividad del medio (ε):
En el caso del vacío se cumple que ε=ε0, donde la permitividad del vacío (ε0) equivale a 8.85·10-12 N·m2 / C2.
Para medios distintos del vacío, se utiliza una magnitud adimensional denominada constante dieléctrica relativa o permitividad relativa (εr), que se obtiene por medio del cociente entre la permitividad del medio (ε) y la permitividad del vacío (ε0):
| Medio | εr |
|---|---|
| vacío | 1 |
| Aire seco (sin CO2) | 1.00054 |
| Etanol | 25.3 |
| Agua | 80.1 |
| Sal Común | 5.9 |
| Vidrio | 4 - 10 |
| PVC | 3.4 |
Ley de CoulombCargas iguales se repelen, cargas diferentes se atraen.La fuerza eléctrica que actúa sobre una carga puntual q1 como resultado de la presencia de una segunda carga puntual q2 esta dada por la ley de Coulomb:donde ε0 = permitividad del vacío Note que esto satisface la tercera ley de Newton porque implica que sobre q2, actua exactamente la misma magnitud de la fuerza. La ley de Coulomb es una ecuación vectorial e incluye el hecho de que la fuerza actúa a lo largo de la línea de unión de las cargas. Cargas iguales se repelen y cargas distintas se atraen. La ley de Coulomb describe una fuerza de alcance infinito que obedece la ley del inverso del cuadrado, y es de la misma forma que la ley de la fuerza de la gravedad.
| Índice Fuerza Electromagnética | ||
| Atrás |
Ejemplo de Fuerza EléctricaLa fuerza eléctrica entre cargas se puede calcular usando la ley de Coulomb. Los circuitos domésticos normales en los EEUU, operan con un voltajeAC de alrededor de V =120 voltios. Para tales tipos de circuitos la relación de la potencia eléctrica P = IV nos dice que para usar una potencia de P = 120 vatios en un circuito de 120 voltios, requerirá una intensidad de corriente eléctrica de I = 1 amperio. Un amperio de corriente transporta a través del conductor un culombio de carga por segundo. De modo que un culombio de carga representa la carga transportada a través de una bombilla de 120 vatios en un segundo. Si tuviéramos dos colecciones de cargas de un culombio cada una concentradas en dos puntos separados por un metro de distancia, la fuerza entre ellas se podría calcular de la ley de Coulomb. Para este caso particular el cálculo viene a ser Si de nuestro acuerdo hipotético de distribución de cargas resultan tales enormes fuerzas, entonces ¿por que no vemos manifestaciones dramáticas de las fuerzas eléctricas?. La respuesta general es que en cualquier punto de un cable, no hay mucho mas de una neutralidad eléctrica. La naturaleza nunca acumula un culombio de carga en un punto. Podría ser instructivo examinar la cantidad de carga en una esfera de cobre con un volúmen de un centímetro cúbico. El cobre tiene un electrón de valencia fuera de las capas completas de su átomo y este electrón está bastante libre para poder moverse en el material sólido de cobre, (esto es lo que lo hace un buenconductor eléctrico). La densidad del cobre metálico es de unos 9 gramos/cm3 y un mol de cobre tiene 63,6 gramos, de modo que un centímetro cúbico de cobre contiene alrededor de 1/7 parte de un mol o alrededor de 8,5 x 1022 átomos de cobre. Con un electrón movil por átomo y con la carga del electrón de 1.6 x 10-19 Culombios, esto significa que hay potencialmente alrededor de 13.600 culombios de cargas móviles en un cm3 de cobre. Supongamos que quitamos suficientes electrones de dos esferas de cobre de modo que haya suficiente carga neta positiva para suspender una de ellas sobre la otra. (sujetaremos la de abajo, entonces la de arriba estará sometida a repulsión por cargas iguales, y a atracción de la gravedad por su masa). ¿Que fracción de carga electrónica debemos quitar?. La fuerza para levantar una de las esferas de cobre, sería su peso, 0,088 Newtons. Asumiendo que la carga neta reside en los puntos mas alejados de las esferas debido a la repulsión de carga, podemos establecer la fuerza de repulsión igual al peso de una esfera. El radio de una esfera de un cm3 es de 0,62 cm., de modo que podemos tratar la fuerza como la de dos cargas puntuales, separadas 2,48 cm. (es decir una separación de dos veces el diámtero de la esfera). Usando la ley de Coulomb, esto requiere una carga de 7,8 x 10-8 culombios. Comparado con la carga total móvil de 13.600 culombios, esto equivale a la eliminación de un solo electrón de valencia de cada 5,7 billones (5,7 x 1012) de cada esfera de cobre. El resultado final es que la eliminación de un solo electrón de los cerca de 6 billones de electrones libres de cada esfera de cobre, causaría la suficiente repulsión eléctrica sobre la parte superior de la esfera para elevarla, ¡venciendo el tirón gravitacional de la Tierra entera!. | Índice Fuerza Electromagnética | ||
| Atrás |
Constante de CoulombCuando se describe la fuerza eléctrica en los átomos y los núcleos, a menudo es conveniente trabajar con el producto de la constante de Coulomb y el cuadrado de la carga del electrón, ya que ese producto aparece en las expresiones de la energía potencial y la fuerza eléctricas. Ese producto en las unidades apropiadas para los procesos nuclear y atómico es: |


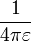
No hay comentarios:
Publicar un comentario