Constantes físicas
El magnetón nuclear (símbolo μN), es una constante física de momento magnético, definido por:
donde:
- e es la carga elemental,
- ħ es la constante de Planck reducida,
- mp es la masa restante del protón.
En unidades SI, su valor aproximado es:
El magnetón nuclear es una unidad natural para expresar los momentos dipolares magnéticos de partículas pesadas tales comonucleones y núcleos atómicos. Por el contrario, el momento dipolar del electrón, que es mucho mayor como consecuencia de un ratio carga-masa mucho mayor, se suele expresar en las unidades correspondientes del magnetón de Bohr.
| nuclear magneton in eV/T | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Value | 3.152 451 2605 x 10-8 eV T-1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Standard uncertainty | 0.000 000 0022 x 10-8 eV T-1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Relative standard uncertainty | 7.1 x 10-10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Concise form | 3.152 451 2605(22) x 10-8 eV T-1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Click here for correlation coefficient of this constant with other constants | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
nuclear-magnetonNotesSymbol
μN
Use "mu-N" for our conversion calculators.
Other Name
magneton-nuclear
Metric (SI) EquivalentAnother Metric (SI) Equivalent with More Basic UnitsStandard UncertaintyMetric (SI) Dimensions
length2 × electric-current
These are the dimensions of the "magnetic moment" quantity in SI units. There are other unit systems used in electromagnetics that may assign different dimensions.
masa de Planck a la cantidad de masa (21,7644 microgramos) que, incluida en una esfera cuyo radio fuera igual a lalongitud de Planck, generaría una densidad del orden de 1093 g/cm³. Según la física actual, esta habría sido la densidad del Universocuando tenía unos
 segundos, el llamado tiempo de Planck. segundos, el llamado tiempo de Planck.
El valor de la masa de Planck
 se expresa por una fórmula que combina tres constantes fundamentales, la constante de Planck (h), la velocidad de la luz (c) y la constante de gravitación universal (G): se expresa por una fórmula que combina tres constantes fundamentales, la constante de Planck (h), la velocidad de la luz (c) y la constante de gravitación universal (G):
siendo
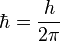 la constante reducida de Planck.- la constante reducida de Planck.- La escala de Planck
Y estaba el señor Max Planck en su sillón académico pensando; ¿por qué las constantes fundamentales de la Naturaleza como la velocidad de la luz, la constante gravitatoria de Newton y la constante fundamental de la teoría cuántica (que él mismo había descubierto) tienen valores tan complicados:
c = 2,99×108 m s-1 (velocidad de la luz)
G = 6,7×10-11 m3 kg-1 s-2 (constante de la gravitación universal)
h = 6,34×10-34 kg m2 s-1 (constante de Planck)
Veamos; hay tres unidades básicas que describen longitud, masa y tiempo (metro, kilogramo, segundo), y también tres constantes fundamentales. Pero, ¿existe un sistema de unidades en el que las tres constantes fundamentales de la física sean iguales a uno? Esto simplificaría mucho las ecuaciones. Vamos a ver…
(calcular, calcular, calcular…)
Pues sí, existe:

Y qué valores tan inimaginables toman el tiempo y la longitud! Pero, en fin, llamaré a este sistema, el sistema de unidades naturales.
Planck falleció en 1947, no vivió lo suficiente como para ser testigo de la importancia que alcanzaría su propuesta. Y es que, cuando los físicos teóricos se propusieron trabajar en la unificación de las dos grandes teorías científicas del siglo XX (la Relatividad General y la Mecánica Cuántica) enseguida vieron que se adentraban en el mundo de la escala de Planck (cómo ahora se denomina en su honor).
Como sabes, en la teoría de la Relatividad General de Einstein, el espacio-tiempo es una estructura extensible y deformable, que se comba o alabea por efecto de los cuerpos con masa. Pero, cómo se ve el espacio-tiempo desde la perspectiva cuántica en la que todas las magnitudes que pueden fluctuar lo hacen. Pues bien, si pudiéramos mirar a través de un microscopio muy potente (un gigantesco acelerador de partículas) veríamos como el espacio se retuerce en convulsas agitaciones formando nudos y lazos fugaces. Para apreciar esta extraña textura fluctuante deberíamos ser capaces de discernir características del tamaño de la longitud de Planck. Ésta es la escala de la textura cuántica del espacio.
¿Y cuál es la escala de tiempo en la que tienen lugar dichas fluctuaciones del tejido espacio-tiempo? Pues, efectivamente, el tiempo de Planck. De hecho, muchos físicos piensan que la longitud y el tiempo de Planck son los cuantos del espacio y el tiempo, por lo que distancias e intervalos más reducidos no deberían de ser posibles.
¿Y cuál es el papel de la masa de Planck? Para ello, imagina dos partículas que colisionan con tanta violencia como para formar un agujero negro en el punto de impacto. La energía necesaria para que esto suceda es (recuerda la equivalencia entre masa y energía: E = mc2), cómo no, la masa de Planck. No es una cantidad extraordinaria, corresponde, más o menos, a la que contiene un depósito de gasolina de un automóvil corriente. Pero concentrar esa energía en dos partículas elementales que colisionan… eso sí sería una hazaña.
El mundo de la escala de Planck es un lugar muy poco conocido, donde la geometría está cambiando constantemente, el espacio y el tiempo son apenas reconocibles y las partículas reales de alta energía están colisionando continuamente y formando minúsculos agujeros negros que no duran más que un simple tiempo de Planck. Pero es el mundo en el que los teóricos de cuerdas pasan sus días de trabajo.
¿Qué le pasa a la singularidad en un agujero negro tras su evaporación por radiación de Hawking? Hay tres opciones: desaparece sin más, queda una singularidad desnuda o queda un remanente. Este último caso sugiere que el remanente podría existir antes de la evaporación. Carlo Rovelli especula que al final del colapso de una estrella no se forma una singularidad dentro del agujero negro, sino una estrella de Planck. Esta estrella tendría una densidad igual a la densidad de Planck, pero su radio sería enorme comparado con la escala de Planck, por ello no es necesario recurrir a una teoría cuántica de la gravedad para describir una estrella de Planck. Una especulación realmente sugerente de un experto en gravedad cuántica de bucles. El artículo técnico es Carlo Rovelli, Francesca Vidotto, “Planck stars,” arXiv:1401.6562 [gr-qc].
Una estrella de Planck tiene una densidad de Planck
Una estrella debe tener una mecanismo que la estabilice, que genere presión que combata a la gravedad. ¿Qué mecanismo proponen Rovelli y Vidotto? Ninguno. No es necesario ninguno. Una respuesta sorprendente donde las haya. La vida media de una estrella de Planck es muy corta medida en su tiempo propio. Sin embargo, gracias a la dilatación temporal, para un observador que se encuentre en el interior del agujero negro, su formación duraría más tiempo que el necesario para que el agujero negro se evaporase al emitir radiación de Hawking. El problema más escabroso resuelto de la manera más trivial posible.
¿Qué pasa cuando un agujero negro con una estrella de Planck se evapora por radiación de Hawking? El radio de la estrella de Planck crecerá al tiempo que el radio del horizonte de Schwarzschild decrecerá, hasta que llegue un momento en que ambos coincidan (como indica esta figura en coordenadas Eddington-Finkelstein). A partir de ese momento se producirá de forma efectiva la evaporación del agujero negro y sólo quedará como remanente la estrella de Planck.
La nueva propuesta de Rovelli y Vidotto tiene la ventaja de que resuelve la paradoja de Hawking asociada a la pérdida de información en los agujeros negros, siendo además compatible con la idea de la complementaridad de los agujeros negros. ¿Cómo evita la necesidad de la aparición de un “muro de fuego” (firewall tipo AMPS) en la edad de Page antes de la evaporación? Muy fácil, la existencia de la estrella de Planck reduce el tiempo de evaporación hasta exactamente el tiempo de Page, luego el argumento AMPS a favor del firewall no se aplica. Toda la información cuántica que se tendría que evaporar entre la edad de Page y el momento de la evaporación queda contenida dentro de la estrella de Planck. No se viola la unitariedad y todo el mundo contento.
Por supuesto, la idea de las estrellas de Planck es muy especulativa y el artículo de Rovelli y Vidotto sólo ofrece estimaciones grosso modo. Habrá que esperar al desarrollo de modelos más detallados (basados en teoría de cuerdas o en gravedad cuántica de bucles) que confirmen o refuten estas estimaciones.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
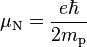
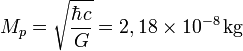
No hay comentarios:
Publicar un comentario