Magnitudes electromagnéticas
admitancia (Y) de un circuito es la facilidad que este ofrece al paso de la corriente. Fue Oliver Heaviside quien comenzó a emplear este término en diciembre de 1887.
En el SI, la unidad de la admitancia es el Siemens, que antiguamente era llamada mho, proveniente de la unidad de resistencia, Ohm, escrita a la inversa.
Al igual que la impedancia, la admitancia se puede considerar cuantitativamente como un valor complejo:
En forma binómica o rectangular, la admitancia vale:
A G se la denomina conductancia y a B susceptancia. Cabe señalar que algunos libros usan la expresión alternativa  .
.
 .
.
Usando la forma binómica o rectangular de  :
:
 :
:
Multiplicando numerador y denominador por "R - jX" y operando resulta:
Expresión que permite definir las componentes real e imaginaria de la admitancia en función de los valores resistivo, R, y reactivo, X, de la impedancia:
Si fueran conocidas las componentes G y B de la admitancia, y a partir de ellas se quieren determinar los valores de R y X de la impedancia, puede demostrarse que:
En los análisis de circuitos en paralelo se suele utilizar la admitancia en lugar de la impedancia para simplificar los cálculos.
Los parámetros de admitancia Y pueden obtenerse de los parámetros de dispersión S como muestran las siguientes expresiones.
Donde
Dichas expresiones normalmente utilizan números complejos para  y para
y para  . Nótese que el valor de
. Nótese que el valor de  puede ser 0 para valores de
puede ser 0 para valores de , por lo que la división por
, por lo que la división por  en los cálculos de
en los cálculos de  puede conllevar una división por 0.
puede conllevar una división por 0.
 y para
y para  . Nótese que el valor de
. Nótese que el valor de  puede ser 0 para valores de
puede ser 0 para valores de , por lo que la división por
, por lo que la división por  en los cálculos de
en los cálculos de  puede conllevar una división por 0.
puede conllevar una división por 0.
En las expresiones, el producto por la impedancia característica  es posible si dicha impedancia no es dependiente de la frecuencia.
es posible si dicha impedancia no es dependiente de la frecuencia.
 es posible si dicha impedancia no es dependiente de la frecuencia.
es posible si dicha impedancia no es dependiente de la frecuencia.
antiferromagnetismo es el ordenamiento magnético de todos los momentos magnéticos de una muestra, durante la aplicación de un campo magnético, en la misma dirección. Al cesar el campo magnético externo la mitad de los momentos magnéticos de la muestra cambian en sentido inverso (por pares, por ejemplo, o una subred frente a otra). Un antiferromagneto es el material que puede presentar antiferromagnetismo. La interacción antiferromagnética es lainteracción magnética que hace que los momentos magnéticos tiendan a disponerse en la misma dirección y en sentido inverso, cancelándolos si tienen el mismo valor absoluto, o reduciéndolos si son distintos. Ha de extenderse por todo un sólido para alcanzar el antiferromagnetismo.
Como el ferromagnetismo, la interacción antiferromagnética se destruye a alta temperatura por efecto de la entropía. La temperatura por encima de la cual no se aprecia el antiferromagnetismo se llama temperatura de Neel, nombrada en honor del químico francés Louis Néel (1904 – 2000), que había identificado por primera vez este tipo de ordenamiento magnético.1 Por encima de esta, los compuestos son típicamente paramagnéticos.
Generalmente, los antiferromagnetos están divididos en dominios magnéticos. En cada uno de estos dominios, todos los momentos magnéticos están alineados. En las fronteras entre dominios hay cierta energía potencial, pero la formación de dominios está compensada por la ganancia en entropía.
Al someter un material antiferromagnético a un campo magnético intenso, algunos de los momentos magnéticos se alinean paralelamente con él, aún a costa de alinearse también paralelo a sus vecinos (superando la interacción antiferromagnética). Generalmente, se requiere un campo magnético muy intenso para conseguir alinear todos los momentos magnéticos de la muestra.
Este fenómeno se explica por la teoría del supercambio, que se basa en que el espín del electrón del átomo metálico induce una polarización en el ligando condicionando al átomo metálico adyacente.
Las interacciones antiferromagnéticas pueden producir momentos magnéticos grandes, incluso imanación. El ferrimagnetismo ocurre en sistemas en los que una interacción antiferromagnética entre momentos magnéticos de diferente magnitud implica un momento magnético resultante grande. La magnetita es un sólido extendido que presenta ferrimagnetismo: es un imán, aunque las interacciones son antiferromagnéticas. El Mn12 es una molécula que presenta el mismo fenómeno: interacciones antiferromagnéticas conllevan un momento magnético grande del estado fundamental. Por otro lado, los sistemas con canteo de espín, con interacciones antiferromagnéticas presentan imanación, por pequeñas desviaciones angulares del alineamiento de los momentos magnéticos, no totalmente antiparalelos.
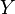 es la
es la 













No hay comentarios:
Publicar un comentario