Funciones aritméticas
ecuación funcional de Cauchy es una ecuación funcional considerada entre las más simples de representar; sin embargo, su solución sobre los números reales es extremadamente complicada. La ecuación es
Sobre los números racionales, puede demostrarse usando álgebra elemental que hay una única familia de soluciones  para cualquier constante c arbitraria.
para cualquier constante c arbitraria.
 para cualquier constante c arbitraria.
para cualquier constante c arbitraria.
Esta familia de soluciones aplica también sobre los reales, pero algunas restricciones adicionales sobre la función f, como las siguientes, pueden resultar en otras soluciones:
- si f es una función continua (probada por Cauchy en 1821). Esta condición fue debilitada en 1875 por Jean Gaston Darboux quien demostró que sólo es necesario que la función sea continua en un punto.
- si f es una función monótona sobre cualquier intervalo.
- si f es una función acotada en cualquier intervalo.
Por otro lado, si no hay condiciones adicionales sobre f, luego (asumiendo el axioma de elección) hay otras infinitas funciones posibles que satisfacen la ecuación. Esto fue demostrado en 1905 por Georg Hamel utilizando las bases de Hamel. El quinto problema de Hilbertes una generalización de esta ecuación.
Ecuaciones Funcionales.
Las ecuaciones funcionales son ecuaciones en las que tenemos una relación entre una función en un punto ó en varios, y sus derivadas ó sucesivas evaluaciones.
Pondremos varios ejemplos para que se puedan ver distintas formas de abordar un problema de este tipo:
Para empezar, como tenemos x e y podemos probar a hacer algunas sustituciones con números.
Lo primero de todo, llamemos  . Entonces es fácil ver que con
. Entonces es fácil ver que con  , obtenemos:
, obtenemos:
Ahora que sabemos los valores de  , podemos probar con
, podemos probar con  :
:
Parece evidente que si  , se cumplirá que
, se cumplirá que  para todo
para todo  , así que intentemos probarlo por inducción.
, así que intentemos probarlo por inducción.
Así que todas las funciones posibles son 
Observación
Las funciones  que cumplen que
que cumplen que  son también
son también  , ya que, sea
, ya que, sea  con
con  , se cumple que
, se cumple que
Hallar todas las funciones  tales que
tales que
Sustituyendo x por y obtenemos que:
Encontrar todas las funciones  tales que
tales que 
(OME-fase nacional 2001)
Supongamos que existe una función  tal que
tal que  .
.
Entonces, si , se cumple que
, se cumple que
Por lo que tenemos que  , y además
, y además 
Pero entonces, haciendo  en la primera igualdad y
en la primera igualdad y  en la segunda, tenemos que
en la segunda, tenemos que  , por lo que
, por lo que  , contradicción con que
, contradicción con que  .
.
Por tanto, no existe ninguna función que cumpla las condiciones del enunciado.
función contador de números primos es una función que cuenta el número de números primos menores o iguales a cierto número real x. Se denota mediante 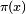 (no debe confundirse con el número π) y analíticamente se define como:
(no debe confundirse con el número π) y analíticamente se define como:
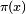 (no debe confundirse con el número π) y analíticamente se define como:
(no debe confundirse con el número π) y analíticamente se define como:
donde # significa la cantidad de números que cumplen la condición. Algunos valores son:
- π(1) = 0 (no hay primos ≤ 1)
- π(2) = 1 (único primo ≤ 2: 2)
- π(3) = 2 (primos ≤ 3: 2 y 3)
- π(4) = 2 (id.)
- π(5) = 3 (primos ≤ 5: 2, 3 y 5)
- ...
- π(10) = 4 (primos ≤ 10: 2, 3, 5 y 7)
- Una de las consecuencias más importantes de la teoría de números es que el valor de π(x) se aproxima al de x/ln x cuando x tiende al infinito. Es decir:
 Esto no significa que la diferencia entre π(x) y x/ln x se aproxime a cero, sino que su cociente se aproxima a 1. Este resultado, aventurado por primera vez por Carl Friedrich Gauss, se denomina teorema de los números primos. Tras muchos intentos fallidos de demostración, los matemáticos Jacques Hadamard y Charles de la Vallée-Poussin consiguieron, de forma independiente, una demostración definitiva.Si se expresa la relación anterior cómo
Esto no significa que la diferencia entre π(x) y x/ln x se aproxime a cero, sino que su cociente se aproxima a 1. Este resultado, aventurado por primera vez por Carl Friedrich Gauss, se denomina teorema de los números primos. Tras muchos intentos fallidos de demostración, los matemáticos Jacques Hadamard y Charles de la Vallée-Poussin consiguieron, de forma independiente, una demostración definitiva.Si se expresa la relación anterior cómo se puede interpretar como que la densidad media de números primos entre los números enteros se aproxima a 1/lnx a medida que xaumenta.25 años después de que Gauss descubriera la aproximación Legendre lo mejoró aún más:
se puede interpretar como que la densidad media de números primos entre los números enteros se aproxima a 1/lnx a medida que xaumenta.25 años después de que Gauss descubriera la aproximación Legendre lo mejoró aún más:
¿Que tiene que ver el número e con los números primos?
Desde los comienzos del blog ciertas constantes han tenido un gran protagonismo en muchos artículos. Cierto es que el númerose lleva la palma, pero pero también ha habidootras constantes a las que se les han dedicado artículos por su importancia y sus características, como
, la constante de Euler-Mascheroni
o el número
.
Sobre este último tenemos varios artículos en los que aparece como protagonista principal o como actor secundario con un papel importante. Por ejemplo, hemos visto que es irracional y que es trascendente, dos características muy interesantes de un número que aparece tanto en nuestra vida diaria (más de lo que muchos piensan). También hablamos de cómo aparece al no formar ninguna pareja en el matching problem y, por otra parte, sabemos que es uno de los componentes de la identidad de Euler.Número eLos primeros 25 números primos
Y qué decir de los números primos, ellos sí que han aparecido en multitud de ocasiones por Gaussianos, ya sea demostrando su infinitud de varias formas (la demostración topológica me parece genial), generándolos o anunciando la aparición de nuevos miembros en esta familia tan peculiar.Lo que no habíamos visto todavía (al menos que yo recuerde) es una relación más o menos clara y directa entre el númeroy los números primos. Vamos, una expresión que involucre a esta constante con este tipo tan especial de números, a este número irracional con estos números tan naturales. Pues ha llegado el momento.
El número
y los números primos
Hace unos días llego al correo de Gaussianos un mail donde Laurato, lector del blog, me informaba sobre una cierta relación entre el númeroy los números primos. En él comentaba que le causó cierta impresión encontrarse con una expresión así y quería saber si había alguna demostración de ese hecho. La relación es la siguiente:
siendoel primorial de
, que es el producto de todos los números primos menores o iguales que
.
El descubridor de esta expresión es el español Sebastián Martín Ruiz, conocido por sus interesantes trabajos sobre teoría de números, centrados principalmente en el estudio de los números primos. Hace unos días estuve dando una vuelta por su web…pero no encontré nada sobre esta expresión.Pero, como no podía ser de otra forma, no me quedé ahí. La curiosidad pudo conmigo y seguí dando vueltas por internet buscando información sobre este curioso límite. Y, por fin, encontré algo. MathWorld me abrió los ojos con su artículo sobre funciones de Chebyshev. En dicho artículo se definen dos funciones llamadas funciones de Chebyshev, pero a nosotros nos interesa solamente una de ellas:En esta expresiónes el logaritmo neperiano,
denota el
-ésimo número primo y
es la función contadora de números primos, que nos da la cantidad de números primos menores o iguales que
.
Operando un poco con la expresión dellegamos a lo siguiente:
De esta funciónse sabe, entre otras cosas, que:
A partir de este límite la demostración de nuestro resultado es coser y cantar. Tomemos, siendo
el
-ésimo número primo. Tenemos entonces lo siguiente:
Por otro lado, usando la última expresión encontrada paratenemos que
Utilizando las dos expresiones anteriores obtenemos lo siguiente:y usando las propiedades de los logaritmosIntercambiando ahorapor
obtenemos
De donde se obtiene la expresión buscada:
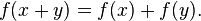

No hay comentarios:
Publicar un comentario