Funciones aritméticas
función de Chebyshov es alguna de dos funciones relacionadas. La primera función de Chebyshov ϑ(x) o θ(x) se expresa como:
con el sumatorio comprendiendo todos los números primos p menores que x. La segunda función de Chebyshov 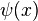 se define como:
se define como:
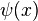 se define como:
se define como:
donde  es la función de von Mangoldt. Se usa frecuentemente la función de Chebyshov en pruebas relacionadas con los números primos, ya que es más fácil de usar que la función contadora de primos,
es la función de von Mangoldt. Se usa frecuentemente la función de Chebyshov en pruebas relacionadas con los números primos, ya que es más fácil de usar que la función contadora de primos,  . Ambas funciones son asintóticas a
. Ambas funciones son asintóticas a  , lo cual equivale alteorema de los números primos.- .....................................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=115cfe0c01b4928a674198bf5bcdc33350f929f5&writer=rdf2latex&return_to=Funci%C3%B3n+de+Chebyshov
, lo cual equivale alteorema de los números primos.- .....................................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=115cfe0c01b4928a674198bf5bcdc33350f929f5&writer=rdf2latex&return_to=Funci%C3%B3n+de+Chebyshov
 es la función de von Mangoldt. Se usa frecuentemente la función de Chebyshov en pruebas relacionadas con los números primos, ya que es más fácil de usar que la función contadora de primos,
es la función de von Mangoldt. Se usa frecuentemente la función de Chebyshov en pruebas relacionadas con los números primos, ya que es más fácil de usar que la función contadora de primos,  . Ambas funciones son asintóticas a
. Ambas funciones son asintóticas a  , lo cual equivale alteorema de los números primos.- .....................................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=115cfe0c01b4928a674198bf5bcdc33350f929f5&writer=rdf2latex&return_to=Funci%C3%B3n+de+Chebyshov
, lo cual equivale alteorema de los números primos.- .....................................................................:https://es.wikipedia.org/w/index.php?title=Especial:Libro&bookcmd=download&collection_id=115cfe0c01b4928a674198bf5bcdc33350f929f5&writer=rdf2latex&return_to=Funci%C3%B3n+de+ChebyshovPolinomios de Chebyshev
Definimos un conjunto de polinomios Tn(x)=cos(nθ) de grado n, donde cosθ=x en el intervalo -1≤x≤1.
Para determinar la forma de estos polinomios recordaremos la fórmula cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
Los primeros polinomios son:
T0(x)=cos(0)=1
T1(x)=cosθ=x;
T1(x)=cosθ=x;
El resto de polinomios se obtiene empleando la relación de recurrencia:
Tn+1(x)=2xTn(x)-Tn-1(x)
T2(x)=cos(2θ)=2x2-1
T3(x)=cos(3θ)=2x(2x2-1)-x=4x3-3x
T4(x)= cos(4θ)=2x(4x3-3x)-( 2x2-1)=8x4-8x2+1
T5(x)= cos(5θ)=2x(8x4-8x2+1)-(4x3-3x)=16x5-20x3+5x
T6(x)= .....
T3(x)=cos(3θ)=2x(2x2-1)-x=4x3-3x
T4(x)= cos(4θ)=2x(4x3-3x)-( 2x2-1)=8x4-8x2+1
T5(x)= cos(5θ)=2x(8x4-8x2+1)-(4x3-3x)=16x5-20x3+5x
T6(x)= .....
Creamos una función recursiva que nos devuelve el valor del polinomio Tn(x) de grado n para valores dados de x.
function y=chebyshev(n,x)
if n==0
y=ones(1,length(x));
elseif n==1
y=x;
else
y=2*x.*chebyshev(n-1,x)-chebyshev(n-2,x);
end
end
Otra forma equivalente de crear una función que nos devuela el valor del polinomio Tn(x) de grado n para valores dados de x es la siguiente:
function T=chebyshev(n,x)
m=length(x);
T=zeros(1,m);
T1=ones(1,m);
T2=x;
for j=2:n
T=2*x.*T2-T1;
T1=T2;
T2=T;
end
end
Mediante el siguiente script, representamos gráficamente los polinomios T1(x), T2(x), T3(x), T4(x) y T5(x)
x=-1:0.01:1;
color=['b' 'g' 'r' 'm' 'k'];
hold on
for n=1:5
y=chebyshev(n,x);
plot(x,y,color(n),'displayName',num2str(n))
end
title('Polinomios de Chebyshev')
xlabel('x')
ylabel('y')
legend('-DynamicLegend','location','Best')
grid on
hold off
Se puede obtener los polinomios de Chebyshev T0(x), T1(x), T2(x), T3(x), T4(x) para valores de x mediante el siguiente código.
n=5;
x=-1:0.01:1; %vector de valores de x
m=length(x);
T=zeros(m,n);
T(:,1)=ones(1,m); %T0(x)
T(:,2)=x; %T1(x)
hold on
for j=3:n %de T2(x) a T4(x)
T(:,j)=2*x'.*T(:,j-1)-T(:,j-2);
end
Creamos una función que nos devuelve el vector de los coeficientes, [a1,a2,...an,an+1], (de mayor a menor grado) del polinomio Tn(x).
function p=chebypoly(n) %n es grado 0,1,2...
p=zeros(n+1,1);
p1=[1];
p2=[1 0];
if n==0
p=p1;
elseif n==1
p=p2;
else
for i=2:n
p=2*[p2 0]-[0 0 p1];
p1=p2;
p2=p;
end
end
end
La función poly2sym de Math Symbolic convierte los coeficientes del polinomio en la expresión algebraicaa1xn+a2xn-1+...anx+an+1. La función ezplot representa gráficamente los polinomios
hold on
color=['b' 'g' 'r' 'm' 'k'];
for n=1:5
Tk=poly2sym(chebypoly(n));
hg=ezplot(Tk,[-1,1]);
set(hg,'color',color(n))
end
hold off
title('Polinomios de Chebyshev')
xlabel('x')
ylabel('y')
grid on
Propiedades de los polinomios de Chebyshev
Los polinomios de Chebyshev están definidos en el intervalo [-1,1].
Simetría
Los polinomios de índice par son funciones pares f(x)=f(-x) y los polinomios de índice impar son funciones impares f(x)=-f(-x)
Raíces
Las raíces del polinomio Tn(x), se obtienen igualando cos(nθ)=0
Observamos que
Obtenemos las raíces del polinomio T5(x) de tres formas distintas:
- Mediante la fórmula que hemos deducido anteriormente,
- Mediante la función roots de MATLAB, si disponemos del vector de los coeficientes del polinomio, que calculamos mediante la función chebypoly
- Mediante la función solve de Math Symbolic que nos proporciona las raíces exactas del polinomio
>> k=1:5;
>> cos((2*k-1)*pi/(2*5))
ans = 0.9511 0.5878 0.0000 -0.5878 -0.9511
>> roots(chebypoly(5))
ans =
0
-0.9511
-0.5878
0.9511
0.5878
>> T5=poly2sym(chebypoly(5))
T5 =16*x^5 - 20*x^3 + 5*x
>> r=solve(T5)
r =
0
(5^(1/2)/8 + 5/8)^(1/2)
(5/8 - 5^(1/2)/8)^(1/2)
-(5^(1/2)/8 + 5/8)^(1/2)
-(5/8 - 5^(1/2)/8)^(1/2)
>> double(r)
ans =
0
0.9511
0.5878
-0.9511
-0.5878
Las raíces del polinomio de grado 5, T5(x), las representamos mediante puntos de color rojo a lo largo del eje X
n=5;
k=1:n;
ang=(2*k-1)*pi/(2*n);
xk=cos(ang);
yk=sin(ang);
hold on
plot(cosd(1:180),sind(1:180),'b')
for i=1:length(xk)
line([0,xk(i)],[0,yk(i)])
hg=line([xk(i),xk(i)],[0,yk(i)]);
set(hg,'linestyle','--');
end
line([-1,1],[0,0])
plot(xk,0,'ro','markersize',4,'markerfacecolor','r')
hold off
axis equal
title('Raíces')
Máximos y mínimos
Los extremos (máximo o mínimo) del polinomio Tn(x)=cos(nθ) donde cosθ=x son 1 y -1, respectivamente.
se producen cuando sin(nθ)=0, es decir nθ=kπ, k=1,2…n-1. En las posiciones.
Se excluye k=0 y k=n por que
>> k=1:4;
>> cos(k*pi/5)
ans = 0.8090 0.3090 -0.3090 -0.8090
>> T5=poly2sym(chebypoly(5))
T5 =16*x^5 - 20*x^3 + 5*x
>> dT5=diff(T5) %calcula la derivada
dT5 =80*x^4 - 60*x^2 + 5
>> r=solve(dT5)
r =
5^(1/2)/4 + 1/4
5^(1/2)/4 - 1/4
1/4 - 5^(1/2)/4
- 5^(1/2)/4 - 1/4
>> y=subs(T5,x,r); %valor del polinomio T5 para cada una de las raíces r.
>> simplify(y)
ans =
-1
1
-1
1
>> double(r)
ans =
0.8090
0.3090
-0.3090
-0.8090
Relaciones entre dos polinomiosTi(x) y Tj(x),
>> syms x; >> T5=poly2sym(chebypoly(5)) T5 =16*x^5 - 20*x^3 + 5*x >> T4=poly2sym(chebypoly(4)) T4 =8*x^4 - 8*x^2 + 1 >> f=T4*T5/sqrt(1-x^2); >> int(f,x,-1,1) ans =0 >> f=T5*T5/sqrt(1-x^2); >> int(f,x,-1,1) ans =pi/2 >> f=1/sqrt(1-x^2); >> int(f,x,-1,1) ans =pi
Relación de ortogonalidad
Como hemos visto, las raíces del polinomio de grado n, Tn(x) son
Sean dos polinomios, Ti(x) y Tj(x), i,j vamos a comprobar que se cumple la siguiente relación que es importante para la aproximación de funciones f(x)
Esta es una relación análoga a la existente en las series de Fourier
n=7; k=1:n; xk=cos((2*k-1)*pi/(2*n)); y5=chebyshev(5,xk); y4=chebyshev(4,xk); suma=sum(y5.*y4) suma=sum(y5.*y5) suma=sum(y4.*y4)
En la ventana de comandos obtenemos el siguiente resultado
suma = -2.4980e-015 suma = 3.5000 suma = 3.5000
De otra forma, mediante la función chebpoly
>> n=7; >> k=1:n; >> xk=cos((2*k-1)*pi/(2*n)); >> T5=chebypoly(5); >> T4=chebypoly(4); >> suma=sum(polyval(T5,xk).*polyval(T4,xk)) suma = -1.2768e-015 >> suma=sum(polyval(T5,xk).*polyval(T5,xk)) suma = 3.5000 >> suma=sum(polyval(T4,xk).*polyval(T4,xk)) suma = 3.5000
Utilizando Math Symbolic obtenemos valores exactos
>> syms x;
>> T5=poly2sym(chebypoly(5));
>> T4=poly2sym(chebypoly(4));
>> n=sym('7'); %raices del polinomio T7
>> k=1:n;
>> xk=cos((2*k-1)*pi/(2*n));
>> suma=sum(subs(T5,x,xk).*subs(T4,x,xk))
suma =0
>> suma=sum(subs(T5,x,xk).*subs(T5,x,xk));
>> simplify(suma)
ans =cos(pi/7) - cos((2*pi)/7) + cos((3*pi)/7) + 3
>> double(ans)
ans = 3.5000 %que es n/2
>> suma=sum(subs(T4,x,xk).*subs(T4,x,xk));
>> simplify(suma)
ans =cos((2*pi)/7) - cos(pi/7) - cos((3*pi)/7) + 4
>> double(ans)
ans = 3.5000 %que es n/2
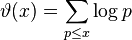

No hay comentarios:
Publicar un comentario