Constantes físicas
En física, la carga de Planck ( ), es una de las magnitudes básicas del sistema del sistema de unidades de Planck. Se trata de una medida de carga eléctrica, definida en base a constantes universales.
), es una de las magnitudes básicas del sistema del sistema de unidades de Planck. Se trata de una medida de carga eléctrica, definida en base a constantes universales.
 ), es una de las magnitudes básicas del sistema del sistema de unidades de Planck. Se trata de una medida de carga eléctrica, definida en base a constantes universales.
), es una de las magnitudes básicas del sistema del sistema de unidades de Planck. Se trata de una medida de carga eléctrica, definida en base a constantes universales.
La carga de Planck se define como:
donde:
 es la velocidad de la luz en el vacío,
es la velocidad de la luz en el vacío, es la constante de Planck,
es la constante de Planck, es la constante de Planck reducida,
es la constante de Planck reducida, es la permitividad del vacío,
es la permitividad del vacío, es la carga elemental,
es la carga elemental, = (137.03599911)−1 es la constante de estructura fina.
= (137.03599911)−1 es la constante de estructura fina.
La carga de Planck es  veces mayor que la carga del electrón.
veces mayor que la carga del electrón.
 veces mayor que la carga del electrón.
veces mayor que la carga del electrón.
Realiza primero las actividades con el applet propuestas en este enlace para familiarizarte con su manejo y comprender el efecto fotoléctrico.Con la ayuda del applet vamos a calcular la constante de Plank. Repite el montaje visto en las actividades y realiza en tu libreta o con la ayuda de una hoja de cálculo la gráfica y los cálculos que te propongo más abajo. Puedes realizar estos mismos cálculos con los applets aquí contenidos.Breve repaso de teoríaMediante una fuente de potencial variable, tal como se ve en la figura podemos medir la energía cinética máxima de los electrones emitidos.Aplicando una diferencia de potencial V variable entre las placas A y C, podemos obtener un potencial que frene el movimiento de los fotoelectrones emitidos – potencial de corte –. Para un voltaje V determinado, el amperímetro no señala paso de corriente, lo que significa que ni los electrones más rápidos llegan a la placa C. En ese momento la energía potencial de los electrones se hace igual a la energía cinética.Millikan realizó el estudio de la relación entre el potencial de corte -V0- y la frecuencia de la luz incidente iluminando diferentes metales.Variando la frecuencia n, (o la longitud de onda de la radiación que ilumina la placa) obtenemos un conjunto de valores del potencial de corte que frenan el paso de electronesV0. Los llevamos a un gráfico (potencial de corte – frecuencia) y obtenemos una serie de puntos. Trazamos la recta de unión intermedia.En realidad estamos representando la energía cinética máxima de los electrones frente a varias frecuencias de luz incidente.Voe=½ m v2. El potencial multiplicado por "e" (carga del electrón) es igual al trabajo. Se denomina energía máxima por fotoelectrón:Vo· e=hn- hnono (frecuencia umbral) , es la frecuencia mínima de la luz necesaria para extraer electrones de un metal dado.
Le corresponde una energía :
hno=trabajo de extracción= fDividiendo la expresión anterior por "e" (carga del electrón) la ecuación que representamos es:
V o=hn / e - hno/ eComparando con una función y=f(x), aquí la "y " es V y la "x" es "n " .
La ordenada en el origen es "hno/ e" y coincide con la energía de arranque en electrón-voltios f / e . La pendiente de la recta es h/e. Midiendo el ángulo de dicha pendiente y usando el valor de la carga del electrón e =1.6 10-19 C, obtenemos el valor de la constante de Planck, h=6.63 10-34 Js.Intensidad eléctrica de Planck
De Wikipedia, la enciclopedia libre
1 - conductores
Fp - Fuerza de Planck
Lp - Longitud de Planck
Ip - Intensidad de PlanckLa intensidad de Planck es la unidad de intensidad eléctrica, denotada por Ip, en el sistema de unidades naturales conocido como las unidades de Planck.Se define como:donde:es la carga de Planck
es el tiempo de Planck
= permitividad en el vacío
es la constante reducida de Planck
- G es la constante de gravitación universal
- c es la velocidad de la luz en el vacío
La intensidad de Planck es aquella que, en un material conductor, lleva una carga de Planck en un tiempo de Planck.También se puede definir como la intensidad constante que, si se mantiene en dos hilos conductores rectos y paralelos de longitud infinita y de radio despreciable, separados entre sí por una distancia de una longitud de Planck en el vacío, se produciría entre estos dos conductores una fuerza igual a una fuerza de Planck por longitud de Planck.- constante cosmológica (denotada usualmente por Lambda,
 ) es una constante propuesta por Albert Einstein como una modificación de su ecuación original del campo gravitatorio para conseguir una solución que diera un universo estático. Einstein rechazó esta idea una vez que el corrimiento observado por Edwin Hubble sugirió que el universo no era estático. Sin embargo, el descubrimiento de la aceleración cósmica en la década de 1990 ha renovado el interés en la constante cosmológica.La constante cosmológica
) es una constante propuesta por Albert Einstein como una modificación de su ecuación original del campo gravitatorio para conseguir una solución que diera un universo estático. Einstein rechazó esta idea una vez que el corrimiento observado por Edwin Hubble sugirió que el universo no era estático. Sin embargo, el descubrimiento de la aceleración cósmica en la década de 1990 ha renovado el interés en la constante cosmológica.La constante cosmológica 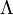 aparece en las ecuaciones de Einstein como:
aparece en las ecuaciones de Einstein como: Cuando
Cuando es cero, estas se reducen a la ecuación tradicional de la relatividad general. Las observaciones astronómicas implican que su valor satisface:
es cero, estas se reducen a la ecuación tradicional de la relatividad general. Las observaciones astronómicas implican que su valor satisface: Aunque Einstein introdujo la constante cosmológica como un término independiente en las ecuaciones del campo gravitatorio, de hecho, éste puede ser interpretado como una energía o presión negativa del vacío. Si se supone que el vacío viene representado por un tensor de energía-impulso dado por:
Aunque Einstein introdujo la constante cosmológica como un término independiente en las ecuaciones del campo gravitatorio, de hecho, éste puede ser interpretado como una energía o presión negativa del vacío. Si se supone que el vacío viene representado por un tensor de energía-impulso dado por: La constante cosmológica es entonces equivalente a una densidad de energía negativa intrínseca del vacío:
La constante cosmológica es entonces equivalente a una densidad de energía negativa intrínseca del vacío: Con su presión negativa asociada. Es frecuente citar los valores de esta densidad de energía directamente como constante cosmológica, aunque en cosmología se suele tomar el signo contrario para la definición de
Con su presión negativa asociada. Es frecuente citar los valores de esta densidad de energía directamente como constante cosmológica, aunque en cosmología se suele tomar el signo contrario para la definición de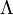 , lo que arroja un valor positivo (ver más abajo).Una constante cosmológica positiva resulta en una densidad de energía negativa y en una presión negativa. La expansión acelerada del universo puede ser atribuida a la presencia de esta energía del vacío diferente de cero.
, lo que arroja un valor positivo (ver más abajo).Una constante cosmológica positiva resulta en una densidad de energía negativa y en una presión negativa. La expansión acelerada del universo puede ser atribuida a la presencia de esta energía del vacío diferente de cero. - La constante cosmológica: ¿el gran error de Einstein?La idea de un universo estático reñía con su constante expansión y la fuerza de la gravedad, dilema que Einstein solucionó al introducir la constante cosmológica, que el científico tildó como su mayor equívoco. Pero grandioso "error", dicen los astrónomos, sin el cual hoy no se entendería el Universo.
Juan Manuel Tejeiro Sarmiento
Profesor Titular del Observatorio Astronómico Nacional de la Universidad Nacional de ColombiaLa "constante cosmológica" fue introducida por Einstein con un alto costo: modificar sin razón física alguna sus ecuaciones. Luego, ante el trabajo de Hubble, por el cual se supo que el Universo está en expansión, Einstein afirmó que haber forzado sus ecuaciones con esta constante había sido el "mayor error de su vida". No obstante, en el modelo cosmológico actual, esta constante tiene una importancia fundamental.Recién formulada la teoría especial de la relatividad en 1905, Albert Einstein (18791955) vio la necesidad de revisar otro de los grandes pilares de la física: la ley de gravitación universal de Isaac Newton (16421727).Esta ley establece que entre todos los cuerpos, independiente de su naturaleza, actúa la fuerza de la gravedad, la cual solo depende de la distancia entre los cuerpos y de la masa de ellos, y de paso implicaba que esta fuerza era instantánea. La ley de gravitación universal era considerada uno de los logros más importantes de la mente humana, pues con su sencillez se podía explicar el movimiento, tanto de los cuerpos en la tierra, como de todos los objetos celestes, con resultados tan extraordinarios como la predicción, en el siglo XIX, de la existencia de un nuevo planeta: Plutón.La razón fundamental que condujo a Einstein a revisar esta ley fue de carácter teórico y no por motivos experimentales u observacionales. Así, el segundo postulado de Einstein de la relatividad especial, sobre la constancia de la velocidad de la luz en el vacío para cualquier observador, tiene, entre otras consecuencias, que ninguna señal o interacción física puede viajar más rápido que la velocidad de la luz. Así la naturaleza instantánea de la ley de gravitación universal de Newton se encontraba en contradicción con este principio.En 1915 Einstein publica su trabajo sobre la teoría general de la relatividad, la cual conduce a cambios aún más profundos en nuestra concepción del espacio y el tiempo, que aquellos que se habían dado con sus trabajos de 1905.Dos célebres resultados que confirmaban su teoría eran: el corrimiento en el perihelio de la órbita de Mercurio y la desviación de la luz por el Sol, corroborada por Arthur Staney Eddintong (18821944) en 1919 en la observación del eclipse total de Sol en ese año.Hasta esta época se consideraba que el Universo era estático. Esta concepción, que ya venía desde los tiempos de Newton, estaba sustentada en las observaciones astronómicas, pues salvo movimientos locales de algunas estrellas o sistemas de estrellas, los objetos celestes observados y estudiados hasta entonces, aparecían fijos en la esfera celeste.¿Cómo explicar el Universo?La fuerza de la gravedad descrita por la ley de gravitación universal es una fuerza atractiva y que actúa entre todos los cuerpos del Universo. ¿Cómo explicar que el Universo observado, con sus estrellas fijas, que ha existido por cientos o miles de millones de años, no haya colapsado por efectos de esa fuerza de atracción universal?Este fue el problema que Einstein abordó en 1915 con su teoría general de la relatividad, partiendo del principio cosmológico: el Universo se asume isotrópico y homogéneo, es decir, el Universo observado es el mismo, sin importar desde qué punto o en cuál dirección se esté observando. A partir de este principio, Einstein emprendió la tarea de resolver sus ecuaciones, modelando la materia del Universo como un fluido de partículas homogéneamente distribuido en el espacio.No obstante, ninguna de las posibles soluciones que encontró a sus ecuaciones le describía un Universo estático. Entonces se dio cuenta que era posible tener una solución estática si a sus ecuaciones les adicionaba un término que llamó "constante cosmológica". El costo era alto: modificar sin razón física alguna sus ecuaciones, pero el Universo así lo exigía.Entre tanto, la astronomía continúa su vertiginoso desarrollo y, en 1929, Edwin Powell Hubble (18891953) anuncia que todas las galaxias se están alejando de nosotros con velocidades proporcionales a la distancia que nos separa de ellas. Este escenario, de un Universo en expansión, era precisamente lo que una de las soluciones de las ecuaciones de Einstein predecía. Por esta época, Einstein comentó que haber forzado sus ecuaciones, con una "constante cosmológica", había sido el mayor error de su vida.De nuevo la constanteLa "constante cosmológica" emerge de nuevo en el campo de la física en la década de 1960 con los trabajos de Iakov Zeldovich (19141987). El contexto era otro, entender la física de las partículas elementales y las fuerzas fundamentales que rigen el micromundo: fuerte, débil y electromagnética. Las teorías de partículas elementales predicen la existencia de una energía mínima de los sistemas, llamada la energía del vacío. ¿Cómo medir esta energía? Pues en los procesos físicos usuales lo que se mide son los cambios de energía del sistema, pero no es posible medir su valor mínimo por definición.Debido a una de las predicciones fundamentales de la teoría especial de la relatividad de Einstein -la equivalencia masaenergía (E=mc2), y al principio de equivalencia entre la masa inercial y la gravitacional, enunciado por Galileo Galilei (15641642), que establece que todos los cuerpos sobre la tierra caen con la misma aceleración, Zeldovich propuso que esa energía del vacío se podía medir gravitacionalmente. Es decir, esa energía debe ejercer fuerza gravitacional y mostró que si esta energía del vacío se consideraba como parte de la masa gravitacional del Universo, entonces las ecuaciones de Einstein de la relatividad general debían contener un término que diera cuenta de esta energía y que tuviera exactamente la forma de la "constante cosmológica", que Einstein había introducido sin justificación alguna en 1915.La "constante cosmológica" representa hoy día un papel fundamental, tanto en el contexto de la física teórica, como en la astronomía, astrofísica y cosmología. En efecto, técnicas observacionales recientes basadas en lentes gravitacionales han permitido determinar para esta constante un valor diferente de cero. Las implicaciones de la "constante cosmológica" hasta ahora se están comenzando a entender, y si sobrevive o no a los nuevos desarrollos de la ciencia, no le quitará el papel importante que ella ha desempeñado en el entendimiento de nuestro Universo actual, y en este sentido "el mayor error de Einstein" en la actualidad es una de sus contribuciones más significativas.

 , por lo tanto
, por lo tanto 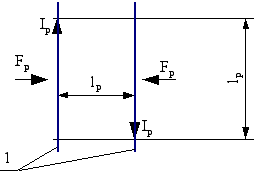

 es la
es la  es el
es el 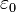 =
=  es la
es la
No hay comentarios:
Publicar un comentario