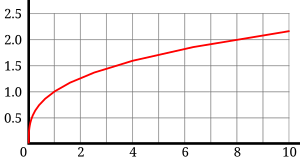
La raíz cúbica, en el sistema de los números reales, estrictamente, es la función inversa de la función (potencia de tercer grado). La extracción de la raíz cúbica de cualquier número real puede admitirse como una operación unaria de los reales en los reales. 12
La operación de calcular la raíz cúbica se puede efectuar, sin restricciones, en el campo ordenado de los números reales, ciertamente, con aproximaciones decimales prefijadas en la mayoría de los casos. Es asociativa con la potenciación y distributiva respecto la multiplicación y división de números reales, pero no es asociativa ni distributiva con la adición o la resta.La raíz cúbica mantiene el signo del radicando.
Históricamente, el famoso problema de la duplicación del cubo, estudiado por Arquitas de Tarento, plantéo la solución a través de la raíz cúbica de 2. Esta cuestión no se resolvió con la aritmética de los números racionales, tampoco con la construcción geométrica a través de regla y compás.3
Para facilitar el cálculo de la raíz cúbica, se hacía uso de logaritmos y sus propiedades sobre las raíces usando tablas y también mediante la regla de cálculo; En la actualidad, se trabaja con las calculadoras.
Definición formal[editar]
Las raíces cúbicas de un número x son números y que satisfacen la ecuación
Números reales[editar]
Si x e y son reales, entonces existe una única solución tal que la ecuación tiene además una única solución, y ésta corresponde a un número real. Si se emplea esta definición, la raíz cúbica de un número negativo es también un número negativo. De esta forma, la raíz cúbica de x es representada igualmente por:
Si x e y son ambos complejos, entonces se puede decir que posee tres soluciones (si x es no nulo) y así x tiene tres raíces cúbicas: una raíz real y dos complejas, en la forma de par conjugado. Este hecho deja interesantes resultados dentro de las matemáticas. Por ejemplo, las raíces cúbicas del número uno son:
Estas dos raíces se relacionan con todas las otras raíces cúbicas de otros números. Si un número es raíz cúbica de un número real las raíces cúbicas pueden ser calculadas multiplicando el número por las raíces de la raíz cúbica de uno.5
Números complejos[editar]
En el cuerpo de los números complejos, la raíz cúbica responde a la solución de la ecuación
donde a es cualquier número complejo no nulo. El conjunto solución involucra tres valores distintos; si z es un complejo real uno de los valores es número real; los otros dos son complejos, sin ninguna parte nula. 6
Para los números complejos, el valor principal de las raíces cúbicas se define como:
Donde Log(z) es la rama principal del logaritmo complejo. Si se escribe z como
Donde r es un número real positivo y cae en el rango:
- ,
entonces la raíz cúbica es
- .
Esto significa que en coordenadas polares al tomar la raíz cúbica de un número complejo se está tomando la raíz cúbica del radio y el ángulo polar se está dividiendo en tres partes de tal forma que define las tres raíces. Con esta definición, la raíz cúbica de un número negativo es un número complejo, y por ejemplo no será -2, sino . En aquellos programas que aceptan resultados imaginarios (tales como Mathematica), el grafo de la raíz cúbica de x en el plano de los números reales dará como resultados valores negativos de la raíz por igual.
Métodos numéricos[editar]
El método de Newton es un método iterativo que puede ser usado para calcular la raíz cúbica. Para números reales representados mediante coma flotante, este método se reduce al siguiente método iterativo para producir sucesivas mejores aproximaciones de la raíz cúbica de a:
El método es simplemente un promedio de tres factores elegidos de tal manera que
en cada iteración.
¿Cómo calcular la raíz cúbica de un número sin calculador, ni tabla de cuadrados?
Al igual que con las raíces cuadradas existe también una operación manual que, aunque muy poco utilizada por haber métodos más sencillos para resolverlas, sirve para hallar el resultado de la raíz cúbica de un número dado.
Veamos de forma práctica cómo utilizar este método calculando la raíz cúbica de 12 910 324.
Para hallar la raíz cúbica de este número natural. |
| 1-Se separan los dígitos de 3 en 3 de derecha a izquierda a la derecha de la coma si no tiene decimales y si los tiene además las cifras decimales se separan de 3 en 3 de izquierda a derecha. | |
| 2-Se determina el número que queda a la izquierda del último grupo, (marcado en rojo). |
En este caso el número a la izquierda del último grupo es 12.
|
| 3-Se busca un número cuyo cubo sea igual o menor (si es menor siempre la cifra más alta posible sin llegar a pasarse) a la primera cifra o conjunto de cifras que se encuentran primero (a la izquierda). |
El cubo perfecto menor que 12 y que más se le aproxima es el número 8.
|
| 4-Hallar la raíz cúbica de ese cubo perfecto. Escribir esta raíz hallada en el espacio destacado que aparece a la derecha de la raíz. | |
| 5-A la primera cifra o conjunto de cifras se le resta ese número cuyo cubo es igual o menor al primer conjunto de cifras, y se pone ese resultado bajándose al lado el siguiente grupo de tres cifras. | |
| 6-Se separan con una coma las dos primeras cifras de la derecha y lo que queda a la izquierda se divide por el triplo del cuadrado de la raíz hallada. | |
| 7-El cociente representara la cifra de las unidades o una cifra mayor. Para probarla se forman tres sumandos que se obtienen de la siguiente manera:
El primer sumando: Es el triplo del cuadrado de la raíz hallada por la cifra que se prueba, multiplicando por 100.
El segundo sumando: Es el triplo de la raíz hallada por el cuadrado la cifra que se prueba, multiplicando por 10.
El tercer sumando: Es el cubo de la cifra que se prueba.
Se efectúan estos productos y se suman. | |
| 8-Si esta suma se puede restar del número del cual separamos las dos primeras cifras de la derecha, la cifra es buena y se sube a la raíz; si no se puede restar se la disminuye una unidad o más hasta que esta suma se pueda restar. | |
| 9-Después de efectuar la resta del producto antes obtenido, a la derecha del resto se escribe el siguiente trío marcado y se repiten las operaciones anteriores hasta bajar el último trío marcado. |
Comprobación 2343 + 97 420 = 12 812 904 + 97 420 = 12 910 324
La raíz cúbica inexacta del número natural 12 910 324 es 234 con resto o residuo 97 420. |
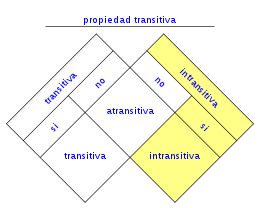
Una relación binaria sobre un conjunto es intransitiva1 cuando se cumple siempre que un elemento se relaciona con otro y este último con un tercero, entonces el primero no se relaciona con el tercero.
Esto es:
Dado el conjunto A y una relación R, esta relación es intransitiva si: y se cumple que .
La propiedad anterior se conoce como intransitividad.
Ejemplos[editar]
Dadas las rectas del plano y la relación binaria perpendicularidad: , entre rectas, que se cumple cuando dos rectas son perpendiculares y no se cumple si no lo son, tenemos que siendo r, s y t rectas del plano P:
Si la recta r es perpendicular a s y s es perpendicular a t, entonces r no es perpendicular a t.
![{\displaystyle {\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a55f866116e7a86823816615dd98fcccde75473)


![{\displaystyle {\sqrt[{3}]{x}}=x^{1 \over 3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d1692c683b6febcb7ff949421d1ad96c487bbf7)
![{\displaystyle {\sqrt[{3}]{1}}={\begin{cases}\ \ 1\\-{\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i\\-{\frac {1}{2}}-{\frac {\sqrt {3}}{2}}i\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8db8661cf785a84afc034139603646124d7a6be7)





![{\displaystyle {\sqrt[{3}]{z}}={\sqrt[{3}]{r}}\exp \left({i\theta \over 3}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/961765e3bd815cb3021b5e874ed1d4c0932919db)
![{\displaystyle {\sqrt[{3}]{-8}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1042604e3bf8b89ddd4771fcc19dbb36b05ce423)











No hay comentarios:
Publicar un comentario