binomio consta únicamente de una suma o resta de dos monomios.
Ejemplos[editar]
- .
- .
- es una diferencia de expresiones trigonométricas.
Binomios notables[editar]
- x2-y2. Diferencia de cuadrados
- x3-y3. Diferencia de cubos
- x3+y3. Suma de cubos
- xn-yn. Diferencia de n-ésimas potencias1
- xn+yn. Suma de n-esimas potencias2
Operaciones con binomios[editar]
Factor común[editar]
El resultado de multiplicar un binomio a+b con un monomio c se obtiene aplicando la propiedad distributiva del producto respecto de la adición:
o realizando la operación:
Esta operación tiene una interpretación geométrica ilustrada en la figura. El área del rectángulo es c(a+b) (el producto de la base por la altura), pero también puede obtenerse como la suma de las dos áreas(ca y cb).
Ejemplo:
Suma por diferencia[editar]
El binomio puede factorizarse como el producto de dos binomios:
- .
Demostración:
Esta disposición suele llamarse diferencia de cuadrados, y es un caso especial de la fórmula: .
Producto de dos binomios lineales[editar]
El producto de un par de binomios lineales es:
- .
Potencia de un binomio[editar]
Un binomio elevado a la n-ésima potencia, se escribe:, y puede desarrollarse utilizando la fórmula de teorema de Newton o, equivalentemente, con ayuda del triángulo de Pascal. El ejemplo más sencillo es el cuadrado perfecto:
Cuadrado de un binomio[editar]
Al elevar un binomio al cuadrado, se lo multiplica por sí mismo:
.
La operación se efectúa del siguiente modo:
De aquí se puede derivar una regla para el cálculo directo: se suman los cuadrados de cada término con el doble producto de los mismos.
Cuando el segundo término es negativo:
La operación se efectúa del siguiente modo:
Ejemplo:
Aplicación en el cálculo diferencial[editar]
Si se quiere hallar la derivada de la función cuadrática , se desarrolla el binomio . El coeficiente del término en que es es la derivada de . Obsérvese que si consideramos el trinomio del desarrollo como dependiente de , el término lineal es .
Igualmente, para se desarrolla . En el cuatrinomio resultante, el coeficiente de es , que es la derivada de .
Un Binomio es una expresión algebraica de dos Términos. Se sabe que los Términos son aquellos valores que están en una suma o resta, al contrario de los Factores, que son los que multiplican o dividen.
Características de los Binomios
Los Términos de un Binomio pueden ser en dos diferentes modalidades: Una variable con una constante, como el Binomio (x+5), ó Dos variables diferentes, como el Binomio (x+y).
En los problemas algebraicos, los Binomios se encontrarán involucrados en una serie de operaciones básicas cuya solución se ha estandarizado. Dichas operaciones se llaman Productos Notables por lo mismo, porque se resuelven mediante la aplicación de una regla o procedimiento general. La ventaja es que se deja de multiplicar término a término para llegar al resultado, lo que es más tardado.
En los Productos Notables, los Binomios pueden estar elevados a un exponente o multiplicándose entre sí en diferentes casos.
Los Binomios y los Productos Notables
Los Binomios se encuentran en cuatro Productos Notables básicos: Binomio al cuadrado, Producto de Binomios Conjugados, Producto de Binomios con un Término Común, y Cubo de un Binomio.
Se explicarán a continuación cada uno de los productos Notables que contienen Binomios, con su procedimiento general:
Binomio al Cuadrado
El Cuadrado del Binomio es el producto de un Binomio por sí mismo. Es posible desarrollar esta operación, multiplicando término a término:
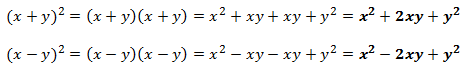
O se puede aplicar la regla general, que reza:
“El cuadrado de un binomio es igual al Cuadrado del Primer Término, más el Doble producto de ambos términos, más el Cuadrado del Segundo Término”.
Y por supuesto se respetarán los signos que precedan a cada término, afectándose así hasta llegar al resultado final, como en la segunda solución.
Producto de Binomios Conjugados
Dos Binomios toman la característica de Conjugados cuando difieren únicamente en el signo de uno de sus términos.
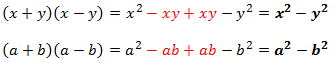
Se pueden ir multiplicando término a término, pero se llega a la conclusión de que el resultado tiene una estructura permanente, que se interpretará así:
“El producto de dos binomios conjugados es igual a la diferencia de los cuadrados de los términos”
Durante la solución del problema, se descubre que los productos de los términos comunes son de signo opuesto, así que terminan eliminándose.
Producto de Binomios con un Término Común
En el Caso de los Binomios con un Término Común, el término común suele ser una variable. Desarrollando el Producto término a término, el resultado queda así:
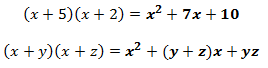
Por tanto, se deduce que el mecanismo de solución es el siguiente:
“El Producto de dos Binomios con un Término Común es igual al Cuadrado del Término Común, más la Suma Algebraica de los No Comunes, multiplicada por el Común, y finalmente más el Producto de los No Comunes”.
Se presenta la solución con Términos No Comunes Constantes, y Variables, para que sea notoria la diferencia entre ambos casos.
Binomio al Cubo
El Binomio al Cubo es aquel Binomio elevado al exponente 3. También es posible desarrollarlo con la multiplicación de Término por Término, pero ese proceso es tardado y confuso, así que lo primero que se resuelve es un Binomio al cuadrado, y al final se multiplica por el tercer Binomio. Lo que sucede es lo siguiente:
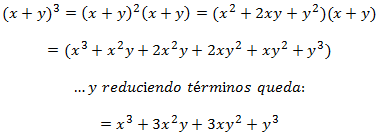
De manera que la Regla General para resolver un Binomio al Cubo se enuncia así:
“El Cubo de un Binomio es igual al Cubo del Primero, más el Triple Producto del Primero Cuadrado por el Segundo, más el Triple Producto del Primero por el Segundo Cuadrado, más el Cubo del Segundo”.
Ejemplos de Binomios
(x+a)
(x+b)
(x+c)
(x+d)
(x+y)
(x+z)
(x+1)
(x+2)
(x+3)
(x+4)
(x+5)
(x+6)
(a+b)
(a+c)
(a+m)
(a+n)
(a+o)
(a+r)
(g+9)
(g+8)
(g+7)
(g+6)
(g+5)
(g+4)
Ejemplos de Binomios en Productos Notables
Binomio al cuadrado
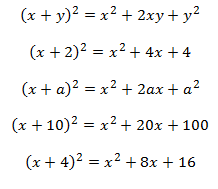
Producto de Binomios Conjugados
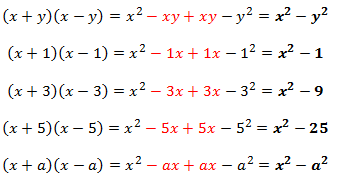
Producto de Binomios con un Término Común
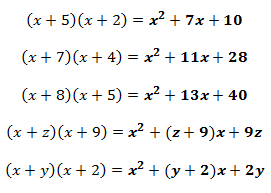
Binomio al Cubo
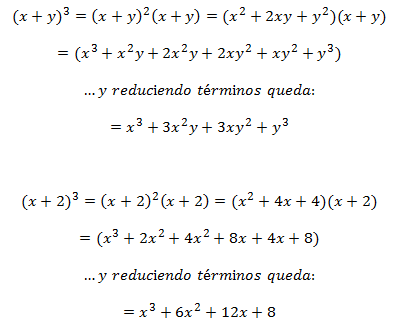

URL del artículo: https://www.ejemplode.com/5-matematicas/4693-ejemplo_de_binomios.html
Fuente: ejemplos de Binomios

































No hay comentarios:
Publicar un comentario