Una ecuación de primer grado o ecuación lineal es una igualdad que involucra una o más variables a la primera potencia y no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia.
|
En todo anillo conmutativo pueden definirse ecuaciones de primer grado.
En una incógnita[editar]
Una ecuación de una variable definida sobre un cuerpo , es decir, con donde x es la variable, admite la siguiente solución:
Cuando tanto la incógnita como los coeficientes son elementos de un anillo que no es un cuerpo, el asunto es más complicado ya que sólo existirán soluciones cuando m divide a n, si el anillo es un dominio de integridad:
En dos incógnitas[editar]
En el sistema cartesiano representan rectas. Una forma común de las ecuaciones lineales de dos variables es:
;
Donde representa la pendiente y el valor de determina el punto donde la recta corta al eje Y (la ordenada al origen).
Algunos ejemplos de ecuaciones lineales:
Formas alternativas[editar]
Formas complejas como las anteriores pueden reescribirse usando las reglas del álgebra elemental en formas más simples. Las letras mayúsculas representan constantes, mientras x e y son variables.
- Ecuación general
-
- Aquí A y B no son ambos cero. Representa una línea en el cartesiano. Es posible encontrar los valores donde x e y se anulan.
- Ecuación segmentaria o simétrica
-
- Aquí ni E ni F no pueden ser cero. El gráfico de esta ecuación corta al eje X y al eje Y en E y Frespectivamente.
- Forma paramétrica
- Dos ecuaciones que deben cumplirse de manera simultánea, cada una en la variable t. Puede convertirse a la forma general despejando t en ambas ecuaciones e igualando. En esta representación puede afirmarse que la recta pasa por el punto y forma con el eje de abcisas un ángulo cuya tangente satisface:
- Casos especiales:
-
- Un caso especial es la forma estándar donde y . El gráfico es una línea horizontal sin intersección con el eje X o (si F = 0) coincidente con ese eje.
- Otro caso especial de la forma general donde y . El gráfico es una línea vertical, interceptando el eje X en E.
- En este caso, todas las variables fueron canceladas, dejando una ecuación que es verdadera en todos los casos. La forma original (no una tan trivial como la del ejemplo), es llamada identidad. El gráfico es todo el plano cartesiano, ya que lo satisface todo par de números reales x e y.
Nótese que si la manipulación algebraica lleva a una ecuación como 1 = 0 entonces la original es llamada inconsistente, o sea que no se cumple para ningún par de números x e y. Un ejemplo podría ser: .
Adicionalmente podría haber más de dos variables, en ecuaciones simultáneas. Para más información véa: Sistema lineal de ecuaciones.
Ecuación lineal en el espacio n-dimensional[editar]
Las ecuaciones lineales de varias variables admiten también interpretaciones geométricas, cuando los coeficientes de la ecuación pertenecen a un cuerpo. Así una función lineal de dos variables de la forma siguiente
representa una recta en un plano. En varias variables asumiendo que tanto las variables y los coeficientes , donde es un cuerpo entonces una ecuación lineal como la siguiente:
representa un hiperplano de n-1 dimensiones en el espacio vectorial n-dimensional .
Sistemas de ecuaciones lineales[editar]
Los sistemas de ecuaciones lineales expresan varias ecuaciones lineales simultáneamente y admiten un tratamiento matricial. Para su resolución debe haber tantas ecuaciones como incógnitas y el determinante de la matriz ha de ser real y no nulo. Geométricamente corresponden a intersecciones de líneas en un único punto (sistema lineal de dos ecuaciones con dos incógnitas), planos en una recta (dos ecuaciones lineales de tres incógnitas) o un único punto (tres ecuaciones lineales de tres incógnitas). Los casos en los que el determinante de la matriz es nulo no poseen solución.
Si se consideran n ecuaciones de primer grado linealmente independientes definidas sobre un cuerpo entonces existe solución única para el sistema si se dan las condiciones del teorema de Rouché-Frobenius, que puede ser calculada mediante la regla de Cramer que es aplicable a cualquier cuerpo. Si las ecuaciones no son linealmente independientes o no se dan las condiciones del teorema la situación es más complicada. Si el sistema se plantea sobre un anillo conmutativo que no sea un cuerpo, la existencia de soluciones es también más complejas.
Linealidad[editar]
Una función definida sobre un espacio vectorial es lineal si y solo si se cumple con la siguiente proposición:
Donde α es cualquier escalar. También se llama a f operador lineal.
Ecuaciones resueltas
En esta sección se resuelven ecuaciones de primer grado cuya dificultad va aumentado: ecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros).
En la Parte I, las ecuaciones son más cortas y se explican todos los pasos. Están ordenadas de menor a mayor dificultad. En la Parte II, las ecuaciones son un poco más complicadas. Y en la Parte III, se muestran todas las operaciones y pasos, pero no se explican tan detalladamente.
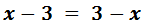
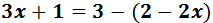
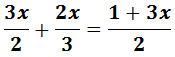
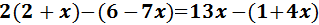
En la Parte I, las ecuaciones son más cortas y se explican todos los pasos. Están ordenadas de menor a mayor dificultad. En la Parte II, las ecuaciones son un poco más complicadas. Y en la Parte III, se muestran todas las operaciones y pasos, pero no se explican tan detalladamente.
Parte I (6 ecuaciones)
Ecuación I.1: ecuación básica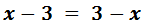
Ver Solución
Pasamos las x's a un lado de la igualdad (izquierda) y los números al otro lado (derecha):
En la derecha, la x está restando. Pasa a la izquierda sumando:
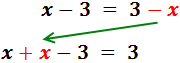 Sumamos los monomios con x’s:
Sumamos los monomios con x’s:
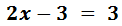 En la izquierda, el -3 está restando. Pasa a la derecha sumando:
En la izquierda, el -3 está restando. Pasa a la derecha sumando:
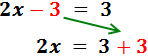 Sumamos los monomios de la derecha:
Sumamos los monomios de la derecha:
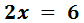 El coeficiente de la x es 2. Este número está multiplicando a x, así que pasa al otro lado dividiendo:
El coeficiente de la x es 2. Este número está multiplicando a x, así que pasa al otro lado dividiendo:
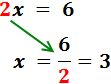 Por tanto, la solución de la ecuación es x = 3.
Por tanto, la solución de la ecuación es x = 3.
Ecuación I.2: ecuación con paréntesisEn la derecha, la x está restando. Pasa a la izquierda sumando:
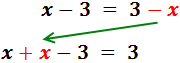
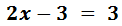
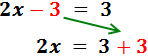
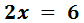
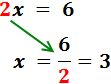
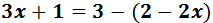
Ver Solución
Recordamos que los paréntesis sirven para agrupar elementos, para simplificar o para evitar ambigüedades.
El signo negativo de delante del paréntesis indica que los monomios que contiene tienen que cambiar de signo:
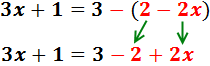 Sumamos 3 y -2 en el lado derecho:
Sumamos 3 y -2 en el lado derecho:
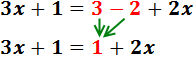 Pasamos los monomios con x’s a la izquierda y los números a la derecha:
Pasamos los monomios con x’s a la izquierda y los números a la derecha:
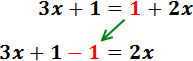 Sumamos 1 y -1. Como el resultado es 0, no lo escribimos:
Sumamos 1 y -1. Como el resultado es 0, no lo escribimos:
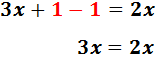 Pasamos 2x a la izquierda restando y sumamos los monomios:
Pasamos 2x a la izquierda restando y sumamos los monomios:
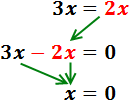 Luego la solución de la ecuación es x = 0.
Luego la solución de la ecuación es x = 0.
Ecuación I.3: ecuación con fraccionesEl signo negativo de delante del paréntesis indica que los monomios que contiene tienen que cambiar de signo:
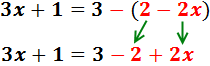
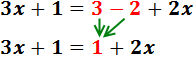
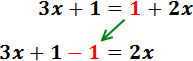
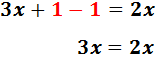
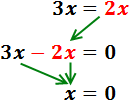
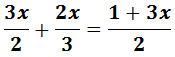
Ver Solución
Tenemos varias formas de proceder con las fracciones:
Multiplicamos, pues, por m.c.m.(2, 3) = 6:
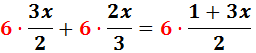 Para simplificar, calculamos las divisiones:
Para simplificar, calculamos las divisiones:
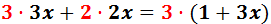 Nótese que hemos escrito un paréntesis al eliminar la fracción de la derecha. Esto se debe a que el 3 debe multiplicar al numerador que está formado por una suma.
Nótese que hemos escrito un paréntesis al eliminar la fracción de la derecha. Esto se debe a que el 3 debe multiplicar al numerador que está formado por una suma.
Calculamos los productos:
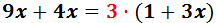 Para eliminar el paréntesis, multiplicamos por 3 todos los elementos que contiene:
Para eliminar el paréntesis, multiplicamos por 3 todos los elementos que contiene:
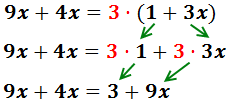 Pasamos las x’s a la izquierda:
Pasamos las x’s a la izquierda:
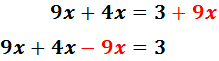 Sumamos los monomios:
Sumamos los monomios:
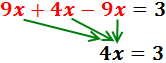 Finalmente, el coeficiente de la x pasa dividiendo al otro lado:
Finalmente, el coeficiente de la x pasa dividiendo al otro lado:
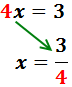 La solución de la ecuación es x = 3/4.
La solución de la ecuación es x = 3/4.
La fracción no se puede simplificar más puesto que ya es irreductible (el máximo común divisor del numerador y del denominador es 1).
Ecuación I.4: ecuación sin solución- Sumar las fracciones de forma habitual.
- Multiplicar la ecuación por el mínimo común múltiplo de los denominadores.
Multiplicamos, pues, por m.c.m.(2, 3) = 6:
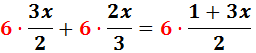
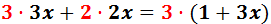
Calculamos los productos:
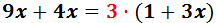
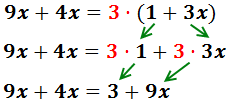
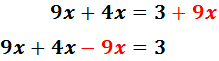
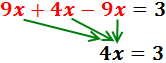
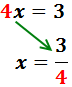
La fracción no se puede simplificar más puesto que ya es irreductible (el máximo común divisor del numerador y del denominador es 1).
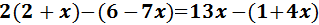
Ver Solución
Eliminamos los paréntesis:
El de la izquierda tiene un 2 delante, por lo que multiplicamos su contenido por 2.
Los otros dos paréntesis tienen un signo negativo delante, así que cambiamos los signos de sus monomios:
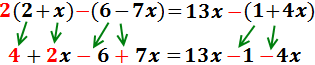 Para simplificar, en cada lado sumamos los monomios con y sin parte literal (los que tienen x y los que no):
Para simplificar, en cada lado sumamos los monomios con y sin parte literal (los que tienen x y los que no):
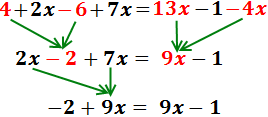 Pasamos las x’s al lado izquierdo y sumamos:
Pasamos las x’s al lado izquierdo y sumamos:
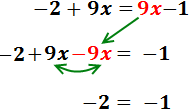 Hemos obtenido una igualdad falsa: -2 = -1. Esto significa que la ecuación nunca se cumple, sea cual sea el valor de x. Por tanto, la ecuación no tiene solución.
Hemos obtenido una igualdad falsa: -2 = -1. Esto significa que la ecuación nunca se cumple, sea cual sea el valor de x. Por tanto, la ecuación no tiene solución.
El de la izquierda tiene un 2 delante, por lo que multiplicamos su contenido por 2.
Los otros dos paréntesis tienen un signo negativo delante, así que cambiamos los signos de sus monomios:
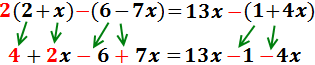
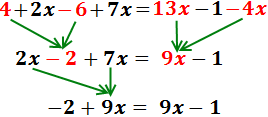
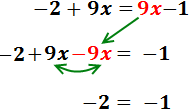





































No hay comentarios:
Publicar un comentario