CONCEPTOS MATEMÁTICOS

Una ecuación de segundo grado¹​²​ o ecuación cuadrática de una variable es una ecuación que tiene la expresión general:

Ecuación de segundo grado ${\displaystyle ax^{2}+bx+c=0\;,\quad a\neq 0}$

donde x es la variable, y a, b y c constantes; a es el coeficientecuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede interpretar mediante la gráfica de una función cuadrática, es decir, por una parábola. Esta representación gráfica es útil, porque las abscisas de las intersecciones o punto de tangencia de esta gráfica, en el caso de existir, con el eje X son las raíces reales de la ecuación. Si la parábola no corta el eje X las raíces son números complejos, corresponden a un discriminante negativo.

Las ecuaciones de segundo grado y su solución de las ecuaciones se conocen desde la antigüedad. En Babilonia se conocieron algoritmos para resolverla. Fue encontrado independientemente en otros lugares del mundo. En Grecia, el matemático Diofanto de Alejandría aportó un procedimiento para resolver este tipo de ecuaciones (aunque su método sólo proporcionaba una de las soluciones, incluso en el caso de que las dos soluciones sean positivas). La primera solución completa la desarrolló el matemático Al-Juarismi (o Al-Khwarizmi según otras grafías), en el siglo IX en su trabajo Compendio de cálculo por reintegración y comparación, cerrando con ello un problema que se había perseguido durante siglos. Basándose en el trabajo de Al-Juarismi, el matemático judeoespañol Abraham bar Hiyya, en su Liber embadorum, discute la solución de estas ecuaciones.^{[cita requerida]} Hay que esperar a Évariste Galois para conseguir resolver en general las ecuaciones polinómicas, o saber cuándo son irresolubles por radicales, que viene a ser una generalización de los métodos de resolución de las ecuaciones de segundo grado.

La primera gran dificultad pudo surgir en la solución de ecuaciones cuadráticas se dio con la ecuación ${\displaystyle x^{2}-2=0}$ en la época de los pitagóricos, al calcular la longitud de la diagonal de un cuadrado de lado 1 ya que no se podía expresar la raíz cuadrada de dos como razón de dos números enteros.³​

En el Renacimiento al resolver ${\displaystyle x^{2}+1=0}$ que requiere hallar un número real cuyo cuadrado sea -1, se superó con la construcción de números imaginarios y la invención de la unidad imaginaria i, definida mediante la igualdad ${\displaystyle i^{2}=-1}$.⁴​⁵​

Soluciones de la ecuación de segundo grado[editar]

Para una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas (si los coeficientes son reales y existen dos soluciones no reales, entonces deben ser complejas conjugadas). Fórmula general para la obtención de raíces:

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$

Se usa ± para indicar las dos soluciones:

${\displaystyle x_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}}$

y

${\displaystyle \ x_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}}$

mostrarDeducción de la solución

Naturaleza de las raíces según el discriminante[editar]

El discriminante es ${\displaystyle \Delta =b^{2}-4ac}$ y sirve para analizar la naturaleza de las raíces que pueden ser reales o complejas.⁶​

Ejemplo del signo del discriminante:

■ ${\displaystyle \Delta >0}$: dos raíces reales distintas. la parábola corta el eje de las abscisas en dos puntos diferentes.

${\displaystyle {\frac {-b+{\sqrt {\Delta }}}{2a}}\quad {\text{y}}\quad {\frac {-b-{\sqrt {\Delta }}}{2a}}.}$

■ ${\displaystyle \Delta =0}$: una raíz real, pero de multiplicidad dos o doble. La parábola solo toca en un único punto al eje de las abscisas.

${\displaystyle -{\frac {b}{2a}}.\,\!}$

■ ${\displaystyle \Delta <0 annotation="">$: dos raíces complejas conjugadas. La parábola no corta al eje de las abscisas.

${\displaystyle {\frac {-b}{2a}}+i{\frac {\sqrt {-\Delta }}{2a}},\quad {\text{y}}\quad {\frac {-b}{2a}}-i{\frac {\sqrt {-\Delta }}{2a}},}$

donde i es la unidad imaginaria.

Coeficiente principal uno en la ecuación completa[editar]

Cuando el término principal o cuadrático no tiene el coeficiente expreso, se sobreentiende que es 1, la ecuación se escribe: ${\displaystyle x^{2}+px+q=0}$ ⁷​, cuyas raíces son:

${\displaystyle x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {{\frac {p^{2}}{4}}-q}}}$

Ecuaciones incompletas[editar]

Sin término independiente[editar]

Son de la forma:

${\displaystyle ax^{2}+bx=0}$, cuyas raíces son ${\displaystyle x_{1}=0;x_{2}={\frac {-b}{a}}}$

Sin término lineal[editar]

Son de la forma ${\displaystyle ax^{2}+c=0}$, cuyas raíces son reales opuestos o imaginarios puros opuestos.

Si ${\displaystyle {\frac {-c}{a}}>0}$ las raíces son reales: ${\displaystyle x_{1}={\sqrt {\frac {-c}{a}}}}$ o ${\displaystyle x_{2}=-{\sqrt {\frac {-c}{a}}}}$

Si ${\displaystyle {\frac {-c}{a}}<0 annotation="">$ las raíces son imaginarias puras: ${\displaystyle x_{1}=i{\sqrt {\frac {c}{a}}}}$ o ${\displaystyle x_{2}=-i{\sqrt {\frac {c}{a}}}}$

Completa con coeficiente lineal par[editar]

En este caso aparece como coeficiente del término de primer grado un número par 2m y la ecuación es

${\displaystyle ax^{2}+2mx+n=0}$

, siendo las raíces

${\displaystyle x_{1,2}={\frac {-m\pm {\sqrt {m^{2}-an}}}{a}}}$

Completa reducida con coeficiente lineal par[editar]

En este caso el coeficiente principal es 1; el coeficiente lineal es par y asume la forma

${\displaystyle x^{2}+2mx+n=0}$

cuyas raíces son

${\displaystyle x_{1,2}=-m\pm {\sqrt {m^{2}-n}}}$

Ecuación bicuadrada[editar]

Éstas son un caso particular de la ecuación de cuarto grado. Les faltan los términos a la tercera y a la primera potencias. Su forma polinómica es:

${\displaystyle ax^{4}+{bx^{2}}^{}+c=0}$

Para resolver estas ecuaciones tan solo hay que hacer el cambio de variable ${\displaystyle {x^{2}}^{}=u}$
Con lo que queda: ${\displaystyle {au^{2}}^{}+bu+c=0}$ El resultado resulta ser una ecuación de segundo grado que podemos resolver usando la fórmula:

${\displaystyle u_{1}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}},\qquad u_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}}$

Al deshacer el cambio de variable aparecen las cuatro soluciones:

${\displaystyle x_{1}=+{\sqrt {u_{1}}}}$

${\displaystyle x_{2}=-{\sqrt {u_{1}}}}$

${\displaystyle x_{3}=+{\sqrt {u_{2}}}}$

${\displaystyle x_{4}=-{\sqrt {u_{2}}}}$

Ecuación bicuadrada simétrica[editar]

Una ecuación bicuadrada simétrica asume la forma:⁸​

${\displaystyle \alpha x^{4}+\beta x^{2}+\alpha =0}$

Ecuación bicuadrada antisimétrica[editar]

Cuando el primer coeficiente y el término independiente son opuestos⁹​

${\displaystyle \alpha x^{4}+\beta x^{2}-\alpha =0}$

Relaciones de raíces y coeficientes[editar]

Partiendo de que tenemos una ecuación cuadrática con raíces ${\displaystyle x_{1},x_{2}\,}$, podemos construir el binomio a partir de estas con:

${\displaystyle (x-x_{1})\cdot (x-x_{2})=0\,}$

${\displaystyle x^{2}-(x_{1}+x_{2})x+x_{1}x_{2}=0\,}$

${\displaystyle ax^{2}-a(x_{1}+x_{2})x+ax_{1}x_{2}=0\,}$

${\displaystyle ax^{2}+bx+c=0\,}$

De lo que se deduce:

Suma de raíces

mostrar${\displaystyle x_{1}+x_{2}=-{\frac {b}{a}}\,}$

Producto de raíces

mostrar${\displaystyle x_{1}\cdot x_{2}={\frac {c}{a}}\,}$

Observación:

mostrar${\displaystyle (x_{1}+x_{2})^{2}-(x_{1}-x_{2})^{2}=4(x_{1}\cdot x_{2})\,}$

${\displaystyle x_{1}^{2}+x_{2}^{2}={b^{2}-2ac \over a^{2}}}$

En el caso de la ecuación ${\displaystyle x^{2}+px+q=0}$ se tiene

${\displaystyle q=x_{1}\cdot x_{2}}$

${\displaystyle \sigma _{1}=x_{1}+x_{2}=-p}$

${\displaystyle \sigma _{2}=x_{1}^{2}+x_{2}^{2}=p^{2}-2q}$

${\displaystyle \sigma _{3}=x_{1}^{3}+x_{2}^{3}=p\cdot (p^{2}-3q)}$

${\displaystyle \sigma _{4}=x_{1}^{4}+x_{2}^{4}=\sigma _{2}^{2}-2q^{2}}$¹⁰​

Relación entre la fórmula general y la proporción áurea[editar]

solo en la solución positiva si en la fórmula general el valor de las variables es el siguiente o se presenta el siguiente caso en que

${\displaystyle a=1,b=-1,c=b}$

entonces la fórmula general dará como resultado el número áureo

${\displaystyle {\frac {-(-1)+{\sqrt {(-1)^{2}-4(1)(-1)}}}{2(1)}}={\frac {1+{\sqrt {5}}}{2}}=\varphi }$

Ecuación trinomia de grado par[editar]

Es una ecuación de la forma ax^2m+bx^m+c=0 , donde usualmente a, b y c son números racionales; a ≠ 0 y m es un número entero no menor de 2.

Para resolver se hace la sustitución x^m= t, con lo que resulta la ecuación original como at²+bt+c=0.

Finalmente de x^m= t se hallan los valores de x mediante x=t^1/m; con seguridad, en el campo de los números complejos, hay 2m raíces.¹¹​

Ejemplo[editar]

La ecuación x⁶+x³+1= 0 (1), la que se obtiene al factorizar la ecuación binomia de noveno grado: x⁹-1= como diferencia de cubos.

Haciendo el reemplazo x³=t, resulta t²+t+1=0, cuyas raíces son precisamente las raíces cúbicas de la unidad: 1, ω, ω². Las sendas raíces cuadradas de estos números complejos son las seis raíces de la ecuación (1).

Ecuaciones de segundo grado

En esta página resolvemos 15 problemas sobre ecuaciones de segundo grado. En la mayoría de los problemas se pide calcular las soluciones de las ecuaciones. Las últimas 4 ecuaciones tienen soluciones complejas.

Recordatorio

La forma general de una ecuación de segundo grado es:

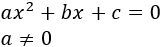
Por comodidad, resolveremos la ecuación de tres formas distintas según los valores de los coeficientes $b$ y $c$.

Se llama discriminante, $\Delta$, a

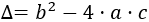
El signo de $\Delta$ nos permite conocer el tipo de soluciones de la ecuación:

• Si $\Delta >0$, hay dos soluciones reales distintas.
• Si $\Delta =0$, hay dos soluciones reales iguales.
• Si $\Delta <0$, no hay soluciones reales (hay dos soluciones complejas distintas).

Caso 1

Si $b$, $c\ne 0$, se dice que la ecuación es completa y sus soluciones las proporciona la fórmula

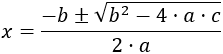
En los siguientes casos, las ecuaciones se dice que son incompletas:

Caso 2

Si $b=0$, la ecuación es de la forma

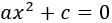
Las soluciones son

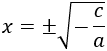
Caso 3

Si $c=0$, la ecuación es de la forma

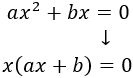
Las soluciones son

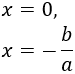
Problema 1

Determinar el tipo y número de soluciones de la ecuación

Solución

Calculamos el discriminante

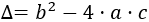Como los coeficientes son $a=3$, $b=-5$ y $c=1$, el discriminante es

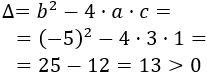El discriminante es positivo, así que la ecuación tiene dos soluciones reales distintas.

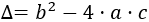
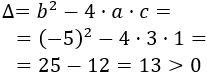
Problema 2

Determinar el tipo y número de soluciones de la ecuación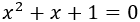

Solución

Calculamos el discriminante

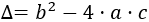Como los coeficientes son $a=1$, $b=1$ y $c=1$, el discriminante es

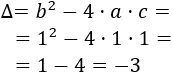El discriminante es negativo, así que la ecuación no tiene soluciones reales (tiene dos soluciones complejas distintas).

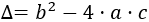
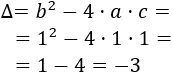
Problema 3

Determinar el tipo y número de soluciones de la ecuación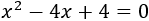

Solución

Calculamos el discriminante

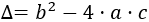Como los coeficientes son $a=1$, $b=-4$ y $c=4$, el discriminante es

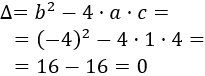El discriminante es negativo, así que la ecuación tiene dos soluciones reales iguales.

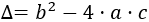
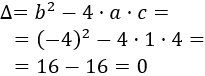
Problema 4

Resolver la ecuación de segundo grado incompleta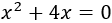

Solución

Es una ecuación incompleta. Factorizamos para calcular las soluciones:

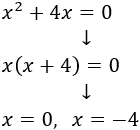La ecuación tiene dos soluciones reales distintas: $0$ y $-4$.

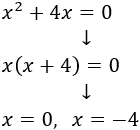
Problema 5

Encontrar las raíces de la función polinómica de segundo grado

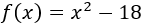
Solución

Las raíces del polinomio $f$ son los valores de $x$ para los que $f\left(x\right)$ es 0, es decir, son las soluciones de la ecuación

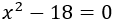
La ecuación es incompleta. La resolvemos:

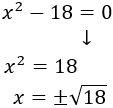
Simplificamos:

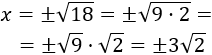
La ecuación tiene dos soluciones reales distintas: $3\sqrt{2}$ y $-3\sqrt{2}$.

https://www.problemasyecuaciones.com/Ecuaciones/segundo-grado/problemas-ecuaciones-segundo-grado-resueltas-solucion-formula-raices-factorizar.html