Algoritmos de factorización de enteros
método de factorización de Dixon (conocido también como método de los cuadrados aleatorios de Dixon1 o algoritmo de Dixon) es unalgoritmo general de factorización de enteros; es el método prototípico de base de factores, y el único método de este tipo para el cual los límites de ejecución no se basan en conjeturas sobre las propiedades de suavidad de los valores de un polinomio conocido.
Historia del algoritmo
Las ideas de este algoritmo provienen de Maurice Kraitchik, quien en la década de 1920 generalizó un famoso método debido a Pierre de Fermat 2 (que funciona bien cuando los factores son cercanos). D. H. Lehmer y R. E. Powers sugirieron una idea parecida en un artículo publicado en 1931 3 , utilizando fracciones continuas.
John Brillhart y Michael Morrison en 1975 4 muestran cómo mejorar el algoritmo utilizando el álgebra lineal sobre 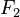 (el cuerpo con dos elementos). John D. Dixonmuestra la eficiencia del algoritmo en un artículo publicado en 1981.5
(el cuerpo con dos elementos). John D. Dixonmuestra la eficiencia del algoritmo en un artículo publicado en 1981.5
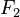 (el cuerpo con dos elementos). John D. Dixonmuestra la eficiencia del algoritmo en un artículo publicado en 1981.5
(el cuerpo con dos elementos). John D. Dixonmuestra la eficiencia del algoritmo en un artículo publicado en 1981.5
El algoritmo de criba cuadrática, debido a Carl Pomerance 6 , utiliza ideas similares a las de este método.
Ideas matemáticas sobre las que se basa
Si 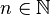 es primo y
es primo y  , entonces la ecuación
, entonces la ecuación  tiene dos soluciones distintas:
tiene dos soluciones distintas: 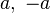 .
.
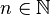 es primo y
es primo y  , entonces la ecuación
, entonces la ecuación  tiene dos soluciones distintas:
tiene dos soluciones distintas: 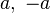 .
.
Sin embargo, si  es compuesto y no es la potencia de un primo, la ecuación
es compuesto y no es la potencia de un primo, la ecuación  tiene más soluciones; estas soluciones vienen de la factorización de
tiene más soluciones; estas soluciones vienen de la factorización de  como producto de dos enteros coprimos entre sí. Si
como producto de dos enteros coprimos entre sí. Si 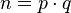 con
con 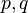 coprimos entonces tomando
coprimos entonces tomando  tal que
tal que  y
y  (esto se puede hacer gracias al Teorema chino del resto) encontramos una solución a
(esto se puede hacer gracias al Teorema chino del resto) encontramos una solución a  que es distinta de
que es distinta de  y
y  .
.
 es compuesto y no es la potencia de un primo, la ecuación
es compuesto y no es la potencia de un primo, la ecuación  tiene más soluciones; estas soluciones vienen de la factorización de
tiene más soluciones; estas soluciones vienen de la factorización de  como producto de dos enteros coprimos entre sí. Si
como producto de dos enteros coprimos entre sí. Si 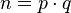 con
con 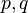 coprimos entonces tomando
coprimos entonces tomando  tal que
tal que  y
y  (esto se puede hacer gracias al Teorema chino del resto) encontramos una solución a
(esto se puede hacer gracias al Teorema chino del resto) encontramos una solución a  que es distinta de
que es distinta de  y
y  .
.
Recíprocamente, si  verifica
verifica  y
y  , entonces
, entonces 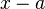 no es coprimo con
no es coprimo con  ni múltiplo de él.
ni múltiplo de él.
 verifica
verifica  y
y  , entonces
, entonces 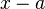 no es coprimo con
no es coprimo con  ni múltiplo de él.
ni múltiplo de él.
La idea básica del algoritmo es intentar encontrar dos enteros  tales que
tales que  y
y  , con lo que
, con lo que  será un divisor de
será un divisor de  no trivial. Buscar al azar estos enteros lleva mucho tiempo y no hace eficaz el método. Lo que se hace para tener más probabilidad de "colisión" es tomar enteros cuyos cuadrados tengan factores primos pequeños.
no trivial. Buscar al azar estos enteros lleva mucho tiempo y no hace eficaz el método. Lo que se hace para tener más probabilidad de "colisión" es tomar enteros cuyos cuadrados tengan factores primos pequeños.
 tales que
tales que  y
y  , con lo que
, con lo que  será un divisor de
será un divisor de  no trivial. Buscar al azar estos enteros lleva mucho tiempo y no hace eficaz el método. Lo que se hace para tener más probabilidad de "colisión" es tomar enteros cuyos cuadrados tengan factores primos pequeños.
no trivial. Buscar al azar estos enteros lleva mucho tiempo y no hace eficaz el método. Lo que se hace para tener más probabilidad de "colisión" es tomar enteros cuyos cuadrados tengan factores primos pequeños.
Más concretamente: tomamos una "base de factores"  formada por enteros pequeños y buscamos
formada por enteros pequeños y buscamos  tales que
tales que  , . . . ,
, . . . ,  . Luego escogemos
. Luego escogemos  de forma que
de forma que  , con cada uno de los
, con cada uno de los  par.
par.
 formada por enteros pequeños y buscamos
formada por enteros pequeños y buscamos  tales que
tales que  , . . . ,
, . . . ,  . Luego escogemos
. Luego escogemos  de forma que
de forma que  , con cada uno de los
, con cada uno de los  par.
par.
Dadas las k-uplas  , . . . ,
, . . . , 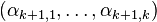 , encontrar
, encontrar  tales que
tales que  sea un producto de elementos de
sea un producto de elementos de  al cuadrado no es otra cosa que obtener una combinación lineal de las k-uplas que sea la nula módulo 2. O sea que es un problema de álgebra lineal en
al cuadrado no es otra cosa que obtener una combinación lineal de las k-uplas que sea la nula módulo 2. O sea que es un problema de álgebra lineal en 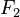 , que puede resolverse en forma rápida.
, que puede resolverse en forma rápida.
 , . . . ,
, . . . , 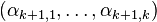 , encontrar
, encontrar  tales que
tales que  sea un producto de elementos de
sea un producto de elementos de  al cuadrado no es otra cosa que obtener una combinación lineal de las k-uplas que sea la nula módulo 2. O sea que es un problema de álgebra lineal en
al cuadrado no es otra cosa que obtener una combinación lineal de las k-uplas que sea la nula módulo 2. O sea que es un problema de álgebra lineal en 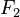 , que puede resolverse en forma rápida.
, que puede resolverse en forma rápida.El método
Sea 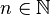 el entero compuesto que deseamos factorizar.
el entero compuesto que deseamos factorizar.
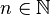 el entero compuesto que deseamos factorizar.
el entero compuesto que deseamos factorizar.
Inicialmente, buscamos enteros  tales que
tales que  se pueda escribir como producto de elementos de
se pueda escribir como producto de elementos de  .
.
 tales que
tales que  se pueda escribir como producto de elementos de
se pueda escribir como producto de elementos de  .
.
Supongamos que hemos encontrado suficientes de estos números (suficientes en general significa poco más que el cardinal de  ):
):  . Utilizamos el álgebra lineal (como se describe en la sección anterior) para encontrar un producto
. Utilizamos el álgebra lineal (como se describe en la sección anterior) para encontrar un producto  que módulo n es el cuadrado de un producto de elementos de
que módulo n es el cuadrado de un producto de elementos de  .
.
 ):
):  . Utilizamos el álgebra lineal (como se describe en la sección anterior) para encontrar un producto
. Utilizamos el álgebra lineal (como se describe en la sección anterior) para encontrar un producto  que módulo n es el cuadrado de un producto de elementos de
que módulo n es el cuadrado de un producto de elementos de  .
.
O sea, hemos obtenido  , o, escribiéndolo de otra manera:
, o, escribiéndolo de otra manera:  . Por lo tanto, el máximo común divisor entre
. Por lo tanto, el máximo común divisor entre  y
y  será distinto de 1 y
será distinto de 1 y  siempre que
siempre que  .
.
 , o, escribiéndolo de otra manera:
, o, escribiéndolo de otra manera:  . Por lo tanto, el máximo común divisor entre
. Por lo tanto, el máximo común divisor entre  y
y  será distinto de 1 y
será distinto de 1 y  siempre que
siempre que  .
.
En caso que  se busca otra combinación lineal que nos dé un producto de cuadrados de elementos de
se busca otra combinación lineal que nos dé un producto de cuadrados de elementos de  .
.
 se busca otra combinación lineal que nos dé un producto de cuadrados de elementos de
se busca otra combinación lineal que nos dé un producto de cuadrados de elementos de  .
.Ejemplo
Sea  . Tomamos
. Tomamos  , por lo que
, por lo que  .
.
 . Tomamos
. Tomamos  , por lo que
, por lo que  .
.
Encontramos varios enteros cuyos cuadrados son factorizados (módulo  ) sobre
) sobre  :
:
 ) sobre
) sobre  :
: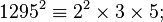



 .
.
Tenemos las 4-uplas: (0,2,1,1), (1,0,1,0), (1,0,1,1), (0,0,1,0) y (1,0,2,1); estos son los exponentes de la factorización de los cuadrados como productos de elementos de  . Al tener 5 4-uplas, debe haber una que sea combinación de las otras (módulo 2); o lo que es lo mismo, una suma de estas 4-uplas tendrá todas sus entradas pares.
. Al tener 5 4-uplas, debe haber una que sea combinación de las otras (módulo 2); o lo que es lo mismo, una suma de estas 4-uplas tendrá todas sus entradas pares.
 . Al tener 5 4-uplas, debe haber una que sea combinación de las otras (módulo 2); o lo que es lo mismo, una suma de estas 4-uplas tendrá todas sus entradas pares.
. Al tener 5 4-uplas, debe haber una que sea combinación de las otras (módulo 2); o lo que es lo mismo, una suma de estas 4-uplas tendrá todas sus entradas pares.
De hecho, la suma de las primeras cuatro da (2,2,4,2). Esto quiere decir que al multiplicar los primeros cuatro números, su cuadrado será  (módulo n). O sea que
(módulo n). O sea que  .
.
 (módulo n). O sea que
(módulo n). O sea que  .
.
Reducimos:  . Esta combinación hallada no nos da ningún factor, ya que
. Esta combinación hallada no nos da ningún factor, ya que  .
.
 . Esta combinación hallada no nos da ningún factor, ya que
. Esta combinación hallada no nos da ningún factor, ya que  .
.
Buscamos otra suma que nos dé con entradas pares: las tres últimas. Obtenemos de allí que  , o lo que es lo mismo:
, o lo que es lo mismo:  . De aquí sí sacamos un factor no trivial de
. De aquí sí sacamos un factor no trivial de  :
:  .
.
 , o lo que es lo mismo:
, o lo que es lo mismo:  . De aquí sí sacamos un factor no trivial de
. De aquí sí sacamos un factor no trivial de  :
:  .
.Tiempo de ejecución
Si en el algoritmo escogemos un  pequeño entonces es fácil saber si un entero se factoriza sobre
pequeño entonces es fácil saber si un entero se factoriza sobre  , pero es difícil encontrar naturales cuyo cuadrado sea producto de elementos de
, pero es difícil encontrar naturales cuyo cuadrado sea producto de elementos de  . A la inversa, si
. A la inversa, si  es grande será sencillo encontrar naturales cuyo cuadrado sea producto de elementos de
es grande será sencillo encontrar naturales cuyo cuadrado sea producto de elementos de  pero complicado saber si un entero se factoriza sobre
pero complicado saber si un entero se factoriza sobre  .
.
 pequeño entonces es fácil saber si un entero se factoriza sobre
pequeño entonces es fácil saber si un entero se factoriza sobre  , pero es difícil encontrar naturales cuyo cuadrado sea producto de elementos de
, pero es difícil encontrar naturales cuyo cuadrado sea producto de elementos de  . A la inversa, si
. A la inversa, si  es grande será sencillo encontrar naturales cuyo cuadrado sea producto de elementos de
es grande será sencillo encontrar naturales cuyo cuadrado sea producto de elementos de  pero complicado saber si un entero se factoriza sobre
pero complicado saber si un entero se factoriza sobre  .
.
La clave para optimizar este método es escoger el valor adecuado de  . Puede probarse que si
. Puede probarse que si  tiene
tiene  dígitos es bueno tomar
dígitos es bueno tomar  con aproximadamente
con aproximadamente  dígitos. Esto hace que el tiempo de ejecución del algoritmo tenga un orden
dígitos. Esto hace que el tiempo de ejecución del algoritmo tenga un orden 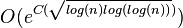 para cierta constante
para cierta constante  . 7 Dixon mostró que podía tomar
. 7 Dixon mostró que podía tomar  , pero Schnorr y Knuth lograron mejorar la prueba, asegurando que
, pero Schnorr y Knuth lograron mejorar la prueba, asegurando que  .
.
 . Puede probarse que si
. Puede probarse que si  tiene
tiene  dígitos es bueno tomar
dígitos es bueno tomar  con aproximadamente
con aproximadamente  dígitos. Esto hace que el tiempo de ejecución del algoritmo tenga un orden
dígitos. Esto hace que el tiempo de ejecución del algoritmo tenga un orden 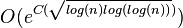 para cierta constante
para cierta constante  . 7 Dixon mostró que podía tomar
. 7 Dixon mostró que podía tomar  , pero Schnorr y Knuth lograron mejorar la prueba, asegurando que
, pero Schnorr y Knuth lograron mejorar la prueba, asegurando que  .
.
El método de factorización de Euler es un método de factorización basado en la representación de un entero positivo  como la suma de dos cuadrados de dos maneras distintas:
como la suma de dos cuadrados de dos maneras distintas:
 como la suma de dos cuadrados de dos maneras distintas:
como la suma de dos cuadrados de dos maneras distintas:
Aunque la factorización algebraica de números binomiales no sirve para factorizar sumas de dos cuadrados (en efecto un número que se puede expresar de una forma como suma de dos cuadrados es un número primo) si se pueden hallar dos representaciones distintas de un número como suma de dos cuadrados se sigue de ahí una factorización:
Partiendo de 

se resta 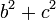 a ambos lados de la igualdad para crear una diferencia de dos cuadrados:
a ambos lados de la igualdad para crear una diferencia de dos cuadrados:
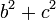 a ambos lados de la igualdad para crear una diferencia de dos cuadrados:
a ambos lados de la igualdad para crear una diferencia de dos cuadrados:
y de ahí se sigue que:
Supóngase sin pérdida de generalidad que  y
y  son ambos pares o bien ambos impares, de forma que su diferencia es par. Ahora se define una constante
son ambos pares o bien ambos impares, de forma que su diferencia es par. Ahora se define una constante  igual almáximo común divisor de
igual almáximo común divisor de  y
y  de forma que:
de forma que:
 y
y  son ambos pares o bien ambos impares, de forma que su diferencia es par. Ahora se define una constante
son ambos pares o bien ambos impares, de forma que su diferencia es par. Ahora se define una constante  igual almáximo común divisor de
igual almáximo común divisor de  y
y  de forma que:
de forma que: y
y 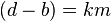 , con
, con 
de forma que, tras sustituir en la expresión anterior quedaría la siguiente ecuación:
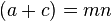 y;
y;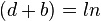
La factorización del número original  se puede mostrar que podría ser igual a:
se puede mostrar que podría ser igual a:
 se puede mostrar que podría ser igual a:
se puede mostrar que podría ser igual a:![N = \left[\left(\frac{k}{2}\right)^2 + \left(\frac{n}{2}\right)^2\right]\cdot(m^2 + l^2)](https://upload.wikimedia.org/math/d/5/9/d59d925932c30609554b0d9b8e27af10.png)
Historia y aplicaciones
La idea de que dos representaciones distintas de un entero positivo diera lugar a una factorización fue aparentemente planteada por primera vez por Marin Mersenne un loco matemático que le gustaba experimentar con los números y letras (Álgebra). Sin embargo, no fue hasta Euler, cien años después y un poco más, que su uso empezara a extenderse. Su más celebrado uso del método que hoy lleva su nombre fue el de factorizar el número , que, al parecer, se pensaba que era primo a pesar de que ninguno de los principales tests de primalidad lo da como pseudoprimo.Como también:se tiene por las fórmulas anteriores:
, que, al parecer, se pensaba que era primo a pesar de que ninguno de los principales tests de primalidad lo da como pseudoprimo.Como también:se tiene por las fórmulas anteriores:a = 1000 a - c = 28 k = 4 b = 3 a + c = 1972 l = 7 c = 972 d - b = 232 m = 58 d = 235 d + b = 238 n = 34 Así,El método de factorización de Euler es más efectivo que el de Fermat para números naturales cuyos factores no sean próximos entre sí y es potencialmente mucho más eficiente que la división por tentativa si se pueden hallar representaciones de números como suma de cuadrados de forma razonablemente fácil. El desarrollo de Euler permitió una factorización mucho más eficiente, y, para los años 1910, el desarrollo de una tabla de factores de números hasta 10 millones. Los métodos empleados para encontrar representaciones de números como sumas de dos cuadrados son esencialmente los mismos que se usan para encontrar las diferencias de cuadrados en el método de Fermat.Desventaja
La gran desventaja del método de factorización de Euler es que no se puede emplear para factorizar un número que tenga algún factor primo de la forma 4k+3 elevado a una potencia impar en su factorización como producto de primos, ya que tal número no podría ser la suma de dos cuadrados. Incluso algunos números compuestosimpares de la forma 4k+1 son el producto de dos primos de la forma 4k+3 (por ejemplo, 3053 = 43 × 71) y por ello no admiten factorización a través del método de Euler.Esta restricción en su uso ha restado protagonismo al método de Euler en el campo de los algoritmos informáticos de factorización, ya que un usuario que intente factorizar un número aleatorio no tiene por qué saber (y en general no sabe) si el método de Euler se puede aplicar a ese número. Sólo recientemente se ha intentado desarrollar el método de Euler en forma de algoritmos informáticos para emplearse en números especiales en los que se sepa que se puede aplicar el método de Euler.- método de factorización de Fermat se basa en la representación de un número natural impar como la diferencia de dos cuadrados:Esa diferencia se puede factorizar algebraicamente como
 ; si ninguno de esos factores es igual a 1, se trata de una factorización propia de n.Todo número impar se puede representar de esta manera. En efecto, si
; si ninguno de esos factores es igual a 1, se trata de una factorización propia de n.Todo número impar se puede representar de esta manera. En efecto, si es una factorización de n, entoncesComo n es impar, c y d también son impares, por lo que su semisuma y semidiferencia son ambos enteros. (Un múltiplo de cuatro también es una diferencia de cuadrados: en ese caso se pueden plantear c y d como números pares.)En su forma más simple, el método de Fermat puede ser incluso más lento que el de división por tentativa en el peor de los casos. Sin embargo, la combinación de división por tentativa y el método de Fermat es más efectivo que el uso exclusivo de uno de ellos.
es una factorización de n, entoncesComo n es impar, c y d también son impares, por lo que su semisuma y semidiferencia son ambos enteros. (Un múltiplo de cuatro también es una diferencia de cuadrados: en ese caso se pueden plantear c y d como números pares.)En su forma más simple, el método de Fermat puede ser incluso más lento que el de división por tentativa en el peor de los casos. Sin embargo, la combinación de división por tentativa y el método de Fermat es más efectivo que el uso exclusivo de uno de ellos. Método básico
Se van tomando varios valores de a, con la esperanza de que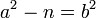 sea un cuadrado.
sea un cuadrado.Algoritmo Factorización de Fermat Entrada: Un número natural impar n. Salida : Un factor del número n.- A ← ⌈√n⌉ // ⌈.⌉ indica la función techo
- Bcuad ← A×A - n
- Mientras Bcuad no sea un cuadrado haga lo siguiente:
- A ← A + 1
- Bcuad ← A×A - n // alternativamente: Bcuad ← Bcuad + 2×A + 1
- Retorne A - √Bcuad // ó A + √Bcuad
Si n tiene más de dos factores primos, este procedimiento primero encuentra la factorización con el menor valor de a y b. Es decir, es el menor factor mayor o igual que la raíz cuadrada de n. Por tanto,
es el menor factor mayor o igual que la raíz cuadrada de n. Por tanto,  es el mayor factor menor o igual que
es el mayor factor menor o igual que 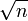 . Si el procedimiento devuelve
. Si el procedimiento devuelve  , entonces n debe ser primo.Para
, entonces n debe ser primo.Para , sea c el mayor factor menor que la raíz.
, sea c el mayor factor menor que la raíz.  , por tanto, el número de pasos requeridos es aproximadamente:
, por tanto, el número de pasos requeridos es aproximadamente: .
.
Si n es primo (es decir,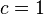 ), ¡hacen falta
), ¡hacen falta  pasos! Esta es desde luego una mala forma de demostrar la primalidad de un número. Pero si n tiene un factor próximo a su raíz cuadrada, el método funciona rápidamente. Concretamente, si c difiere de
pasos! Esta es desde luego una mala forma de demostrar la primalidad de un número. Pero si n tiene un factor próximo a su raíz cuadrada, el método funciona rápidamente. Concretamente, si c difiere de  en menos de
en menos de  , entonces el método sólo necesita un paso, y esto es independiente del tamaño de n.
, entonces el método sólo necesita un paso, y esto es independiente del tamaño de n.Ejemplo
Tómese el número para realizar su factorización, se procede así:
para realizar su factorización, se procede así:A: 78 79 80 Bcuad: 125 282 441 El tercer intento produce un cuadrado. ,
,  , y los factores son
, y los factores son  y
y  .
.Factorización de Fermat y división por tentativa
Intentemos factorizar el número primo n=2345678917, pero también calcular b y a-b. Empezando por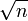 y subiendo desde ahí, quedan así tabulados los datos:
y subiendo desde ahí, quedan así tabulados los datos:A: 48433 48434 48435 48436 Bcuad: 76572 173439 270308 367179 B: 276,7 416,5 519,9 605,9 A-B: 48156,3 48017,5 47915,1 47830,1 En la práctica, se puede ignorar la última fila hasta que b sea un número entero. Pero cabe observar que si n tuviera un factor menor que su raíz pero mayor que , el método de Fermat ya lo habría encontrado.La división por tentativa normalmente tendría que seguir hasta el mayor primo menor que 48432; pero tras sólo cuatro pasos con el método de Fermat, basta intentarlo hasta 47830 para encontrar un factor o determinar la primalidad.Esto sugiere la implementación de un método que combine los ya descritos. Basta tomar una cota
, el método de Fermat ya lo habría encontrado.La división por tentativa normalmente tendría que seguir hasta el mayor primo menor que 48432; pero tras sólo cuatro pasos con el método de Fermat, basta intentarlo hasta 47830 para encontrar un factor o determinar la primalidad.Esto sugiere la implementación de un método que combine los ya descritos. Basta tomar una cota y usar Fermat para los factores comprendidos entre
y usar Fermat para los factores comprendidos entre 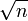 y
y  . Esto deja una cota para la división por tentativa de
. Esto deja una cota para la división por tentativa de  . En el ejemplo anterior, con
. En el ejemplo anterior, con  la cota para la división por tentativa es 47830. Otra opción razonable sería
la cota para la división por tentativa es 47830. Otra opción razonable sería  , que deja una cota de 28937.Siguiendo con el método de Fermat, se obtiene un rendimiento cada vez menor. Así, normalmente uno pararía antes de llegar a este punto:
, que deja una cota de 28937.Siguiendo con el método de Fermat, se obtiene un rendimiento cada vez menor. Así, normalmente uno pararía antes de llegar a este punto:A: 60001 60002 Bcuad: 1254441084 1254561087 B: 35418,1 35419,8 A-B: 24582,9 24582,2 Mejoras del algoritmo
Mejora del cribado
No es necesario computar todas las raíces cuadradas de los , ni siquiera todos los valores de
, ni siquiera todos los valores de  . Por ejemplo, aquí se presenta de nuevo la tabla para
. Por ejemplo, aquí se presenta de nuevo la tabla para  :
:A: 48433 48434 48435 48436 Bcuad: 76572 173439 270308 367179 B: 276,7 416,5 519,9 605,9 Se puede ver rápidamente que ninguno de estos valores de Bcuad es un cuadrado. Los cuadrados son congruentes con 0, 1, 4, 5, 9 ó 16 módulo 20. Los valores se repiten con cada aumento de en 10 unidades. En este ejemplo,
en 10 unidades. En este ejemplo,  produce 3, 4, 7, 8, 12 y 19 módulo 20 para estos valores. De ahí se deduce que sólo el 4 de esta lista puede corresponder a un cuadrado. Por tanto,
produce 3, 4, 7, 8, 12 y 19 módulo 20 para estos valores. De ahí se deduce que sólo el 4 de esta lista puede corresponder a un cuadrado. Por tanto, 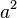 debe ser 1 mód 20, lo que implica que
debe ser 1 mód 20, lo que implica que  es 1 ó 9 mód 10; esto dará lugar a un Bcuad congruente con 4 mód 20, y si Bcuad es cuadrado,
es 1 ó 9 mód 10; esto dará lugar a un Bcuad congruente con 4 mód 20, y si Bcuad es cuadrado,  acabará en 2 u 8 mód 10.Este proceso se puede realizar con cualquier módulo. Con el mismo
acabará en 2 u 8 mód 10.Este proceso se puede realizar con cualquier módulo. Con el mismo ,
,módulo 16: Los cuadrados son 0, 1, 4 ó 9 n mód 16 es 5 así que 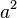 sólo puede ser
sólo puede ser9 y  debe ser
debe ser3 ó 5 módulo 16 módulo 9: Los cuadrados son 0, 1, 4 ó 7 n mód 9 es 7 así que 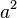 sólo puede ser
sólo puede ser7 y  debe ser
debe ser4 ó 5 módulo 9 Generalmente se toma una potencia de un primo distinto para cada módulo.Dada una sucesión de valores de a (inicial, final y el "paso") y un módulo, se puede proceder así:- Criba_Fermat(n, Aini, Afin, Apaso, Módulo)
- A ← Aini
- hacer Módulo veces:
- Bcuad ← A×A - n
- si Bcuad es cuadrado, módulo Módulo:
- Criba_Fermat(n, A, Afin, Apaso × Módulo, Siguiente_Módulo)
- fin si
- A ← A + Apaso
- fin hacer
Pero se puede detener la recursión cuando quedan pocos valores de a, es decir, cuando (Afin-Aini)/Apaso es pequeño. Además, como el tamaño del paso de a' es constante, se pueden computar los sucesivos Bcuad mediante sumas.Mejoras por uso de multiplicador
El método de Fermat funciona de forma óptima cuando hay un factor cercano a la raíz cuadrada de n. A lo mejor se puede favorecer que así sea.Si se conoce la razón aproximada de dos factores ( ), entonces se puede escoger un número racional
), entonces se puede escoger un número racional  próximo a ese valor.
próximo a ese valor.  , quedando dos factores próximos que el método de Fermat, aplicado a nuv, hallará rápidamente. Entonces
, quedando dos factores próximos que el método de Fermat, aplicado a nuv, hallará rápidamente. Entonces  y
y  . (A menos que c divida a u o d divida a v.)En general, no se conoce esa razón, pero se puede probar con diversos valores
. (A menos que c divida a u o d divida a v.)En general, no se conoce esa razón, pero se puede probar con diversos valores , y tratar de factorizar cada nuv que surja. R. Lehman ideó una forma sistemática de hacer esto, de forma que la combinación de Fermat y la división por tentativa factorice n en
, y tratar de factorizar cada nuv que surja. R. Lehman ideó una forma sistemática de hacer esto, de forma que la combinación de Fermat y la división por tentativa factorice n en  .1
.1Otras mejoras
La idea fundamental del método de Fermat es la base de la criba cuadrática y la criba generalizada sobre el cuerpo de los números (general number field sieve), los algoritmos mejor conocidos para la factorización de semiprimos grandes "en el peor de los casos". La principal mejora de la criba cuadrática sobre la factorización de Fermat es que, en lugar de buscar un cuadrado en la sucesión de a2−n, lo que hace es hallar un subconjunto de elementos de esta sucesión cuyo producto es un cuadrado, y lo hace de forma muy eficiente. El resultado final es el mismo: una diferencia de cuadrados mód n que, si no es trivial, puede emplearse para factorizar n.



 y
y  son
son  es divisible por
es divisible por 
![\begin{align}
1000009 & = \left[\left(\frac{4}{2}\right)^2 + \left(\frac{34}{2}\right)^2\right]\cdot(58^2 + 7^2) \\
{} & = (2^2 + 17^2)\cdot(58^2 + 7^2) \\
{} & = (4 + 289)\cdot(3364 + 49) \\
{} & = 293\cdot3413
\end{align}](https://upload.wikimedia.org/math/5/0/d/50d1d27736a49d8056133b06d1a2029e.png)


No hay comentarios:
Publicar un comentario