sábado, 31 de octubre de 2015

Algoritmos

Algoritmos de precisión arbitraria

algoritmo de multiplicación es un algoritmo (o método) para multiplicar dos números. Dependiendo del tamaño de los números, existen diferentes algoritmos. Los algoritmos de multiplicación existen desde el advenimiento del sistema decimal.

Multiplicación de dos enteros

El algoritmo estándar para multiplicar dos números enteros, requiere el aprendizaje previo de las tablas de multiplicar. La multiplicación se empieza desde la derecha, teniendo cuidado con la ley de los signos y con colocar las unidades de un orden bajo las unidades del mismo orden (unidades bajo unidades, decenas bajo decenas, centenas bajo centenas, etc.). Luego se suman los productos de cada cifra del segundo factor por todas las del primero.

Ejemplo

Sea la multiplicación de 4103 como multiplicando y 254 como multiplicador.
Se coloca el multiplicador debajo del multiplicando, haciendo coincidir las columnas de las unidades por la derecha.
\begin{array}{rrrrrrr} & & & 4 & 1 & 0 & 3 \\ \times & & & & 2 & 5 & 4 \\ \hline \end{array}
Conforme a las tablas elementales, se multiplica la cifra de unidades (4)del multiplicador por cada una de las cifras del multiplicando, empezando por las unidades (3) acarreando, en su caso, las decenas (4 × 3 = 12, acarreo de 1 unidad) como suma al resultado de la multiplicación de la cifra siguiente [(4 × 0) + 1 = 1), 1 de acarreo], continuándose de igual forma con las demás cifras del multiplicando (4103 × 4 = 16412). Consideramos esta línea como línea provisional.
\begin{array}{rrrrrrr} & & & 4 & 1 & 0 & 3 \\ \times & & & & 2 & 5 & 4 \\ \hline & & 1 & 6 & 4 & 1 & 2 \\ \end{array}
Se procede de igual forma con la cifra de las decenas del multiplicador con cada una de las cifras del multiplicando, si bien el resultado se escribe debajo de la fila anterior corriendo un lugar a la izquierda la cifra de las unidades. (4103 × 5 = 20515)
\begin{array}{rrrrrrr} & & & 4 & 1 & 0 & 3 \\ \times & & & & 2 & 5 & 4 \\ \hline & & 1 & 6 & 4 & 1 & 2 \\ & 2 & 0 & 5 & 1 & 5 & \\ \end{array}
Se continúa así con todas las cifras del multiplicador. (4103 × 2 = 8206)
\begin{array}{rrrrrrr} & & & 4 & 1 & 0 & 3 \\ \times & & & & 2 & 5 & 4 \\ \hline & & 1 & 6 & 4 & 1 & 2 \\ & 2 & 0 & 5 & 1 & 5 & \\ & 8 & 2 & 0 & 6 & & \\ \end{array}
Finalmente se suman las cifras de cada una de las líneas provisionales, considerando los huecos de la derecha como ceros.
\begin{array}{rrrrrrr} & & & 4 & 1 & 0 & 3 \\ \times & & & & 2 & 5 & 4 \\ \hline & & 1 & 6 & 4 & 1 & 2 \\ & 2 & 0 & 5 & 1 & 5 & \\ & 8 & 2 & 0 & 6 & & \\ \hline 1 & 0 & 4 & 2 & 1 & 6 & 2 \\ \end{array}
El resultado o Multiplicación es el que resulta de dicha suma (4103 × 254 = 1042162)

Ejemplo 2

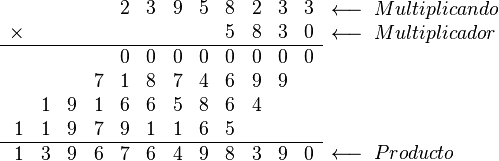
En este ejemplo se utiliza la multiplicación larga de multiplicar 23958233 (multiplicando) por 5830 (multiplicador) y se llega al 139676498390 como resultado del producto.
\begin{array}{rrrrrrrrrrrr} & & & & 2 & 3 & 9 & 5 & 8 & 2 & 3 & 3 \\ \times & & & & & & & & 5 & 8 & 3 & 0 \\ \hline \end{array} \begin{array}{l} \longleftarrow \; Multiplicando\\ \longleftarrow \; Multiplicador\\ \end{array}
Se realizan las operaciones:
\begin{array}{rrrrrrrrrrrr} & & & & 2 & 3 & 9 & 5 & 8 & 2 & 3 & 3 \\ \times & & & & & & & & 5 & 8 & 3 & 0 \\ \hline & & & & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ & & & 7 & 1 & 8 & 7 & 4 & 6 & 9 & 9 & \\ & 1 & 9 & 1 & 6 & 6 & 5 & 8 & 6 & 4 & & \\ 1 & 1 & 9 & 7 & 9 & 1 & 1 & 6 & 5 & & & \\ \hline 1 & 3 & 9 & 6 & 7 & 6 & 4 & 9 & 8 & 3 & 9 & 0 \\ \end{array} \begin{array}{l} \\ \\ \longleftarrow 23 \; 958 \; 233 \times 0\\ \longleftarrow 23 \; 958 \; 233 \times 30 \\ \longleftarrow 23 \; 958 \; 233 \times 800 \\ \longleftarrow 23 \; 958 \; 233 \times 5.000 \\ \\ \end{array}
Que dan como resultado:
\begin{array}{rrrrrrrrrrrr} & & & & 2 & 3 & 9 & 5 & 8 & 2 & 3 & 3 \\ \times & & & & & & & & 5 & 8 & 3 & 0 \\ \hline & & & & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ & & & 7 & 1 & 8 & 7 & 4 & 6 & 9 & 9 & \\ & 1 & 9 & 1 & 6 & 6 & 5 & 8 & 6 & 4 & & \\ 1 & 1 & 9 & 7 & 9 & 1 & 1 & 6 & 5 & & & \\ \hline 1 & 3 & 9 & 6 & 7 & 6 & 4 & 9 & 8 & 3 & 9 & 0 \\ \end{array} \begin{array}{l} \longleftarrow \; Multiplicando\\ \longleftarrow \; Multiplicador\\ \\ \\ \\ \\ \longleftarrow \; Producto \\ \end{array}

Multiplicación hindú o de Fibonacci

En primer lugar, se dibuja la tabla y se escriben los números que se multiplicarán alrededor de las filas y las columnas. A continuación, se rellenan las celdas con las decenas en los triángulos superiores y las unidades en los inferiores.
Por último, se suma siguiendo las líneas diagonales "llevándose" las decenas cuando es necesario, hasta obtener la solución.
La multiplicación hindú o de Fibonacci requiere la preparación de una tabla (una rejilla dibujada en un papel) que sirve de guía para el cálculo. Fue introducida en Europa en 1202 por Fibonacci en su Liber Abaci. Leonardo describió la operación como "cálculo mental", y utilizaba los dedos de las manos para realizar los cálculos intermedios. Napier también publicó este método en 1617, el año en que murió.
Como se muestra en el ejemplo, el multiplicando y el multiplicador se escriben encima y a la derecha de la tabla.
  • Durante la fase de multiplicación, la tabla se rellena con los productos de los dígitos que señalan cada fila y columna, que arrojan números de dos dígitos: las decenas se escriben en la esquina superior izquierda de cada celda, y las unidades en la inferior derecha.
  • Durante la fase de adición, se suma la tabla según las diagonales.
  • Por último, si es necesario "llevarse" las decenas, se muestra la solución de arriba abajo y de izquierda a derecha del borde de la tabla, llevándose las decenas en sentido inverso, como en la multiplicación o en la suma habitual.

Ejemplo

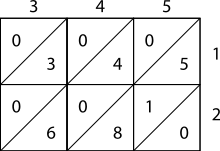
Las imágenes de la derecha muestran cómo calcular 345 × 12 usando la multiplicación hindú. Como ejemplo más complejo, más abajo se muestra el cálculo de 23.958.233 por 5.830; el resultado es 139.676.498.390. Obsérvese que el número 23.958.233 se encuentra en la parte superior de la tabla, y que 5.830 está verticalmente en su lado derecho. Los productos llenan la tabla y la suma de estos productos (diagonalmente) se encuentran en el lado izquierdo y el inferior. A continuación estas sumas se agregan, como se muestra.
     2   3   9   5   8   2   3   3
   +---+---+---+---+---+---+---+---+-
   |1 /|1 /|4 /|2 /|4 /|1 /|1 /|1 /|
   | / | / | / | / | / | / | / | / | 5
 01|/ 0|/ 5|/ 5|/ 5|/ 0|/ 0|/ 5|/ 5|
   +---+---+---+---+---+---+---+---+-
   |1 /|2 /|7 /|4 /|6 /|1 /|2 /|2 /|
   | / | / | / | / | / | / | / | / | 8
 02|/ 6|/ 4|/ 2|/ 0|/ 4|/ 6|/ 4|/ 4|
   +---+---+---+---+---+---+---+---+-
   |0 /|0 /|2 /|1 /|2 /|0 /|0 /|0 /|
   | / | / | / | / | / | / | / | / | 3
 17|/ 6|/ 9|/ 7|/ 5|/ 4|/ 6|/ 9|/ 9|
   +---+---+---+---+---+---+---+---+-
   |0 /|0 /|0 /|0 /|0 /|0 /|0 /|0 /|
   | / | / | / | / | / | / | / | / | 0
 24|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|
   +---+---+---+---+---+---+---+---+-
     26  15  13  18  17  13  09  00

01           
002          
0017         
00024        
000026       
0000015      
00000013     
000000018    
0000000017   
00000000013  
000000000009 
0000000000000
=============
 139676498390

= 139.676.498.390

Implementación en ordenadores

Si un sistema posicional numeral está en uso, un método natural de la enseñanza de la multiplicación de números es impartido en los colegios como multiplicación larga, a veces llamado multiplicación de primaria: multiplicar el multiplicando por cada dígito del multiplicador y después añadir todos los resultados cambiados propiamente. Esto requiere la memorización de la tabla de multiplicar de los dígitos simples.
Los humanos normalmente usan este algoritmo en base 10. Los ordenadores suelen usar un algoritmo similar de “cambiar y añadir” en base 2. Las personas para hacer multiplicaciones largas escribirán todos los productos y después los unirán todos juntos; los ordenadores (y operadores de ábaco) sumarán los productos tan pronto como van siendo calculados.
Algunos chips implementan este algoritmo para el tamaño de varios números enteros y números flotantes en hardware o en micro código. En aritmética de precisión arbitraria es común el uso de las multiplicaciones largas con la base fijada en 2w, donde w es el número de bits en una palabra, para multiplicar números relativamente pequeños.
Para multiplicar dos números con n dígitos usando este método, se necesitan n cuadrado operaciones. Formalmente: usar una métrica de tamaño natural de números de dígitos, el tiempo del algoritmo de complejidad multiplicando dos números de dígitos n usando la multiplicación larga es del orden exacto de n cuadrado Θ(n2).
Cuando son implementados en software, los algoritmos de multiplicación larga tienen que encargarse del desbordamiento durante las sumas (adiciones), que pueden ser caras. Por esta razón, un enfoque típico es representar el número en una base pequeña b como tal, por ejemplo, 8b2 es una representación de números enteros (Richard Brent usó este enfoque en su paquete MP Fortran); podemos entonces llevar a cabo varias sumas antes de tener que encargarnos del desbordamiento. Cuando el número se hace demasiado largo, añadimos parte de él al resultado o lo llevamos y trazamos un mapa de la parte restante hacia un número menor a b; este proceso se conoce como nominalización.

Álgebra: multiplicación de monomios

Para multiplicar monomios no es necesario que sean semejantes. Para ello se multiplican los coeficientes, se deja la misma parte literal y se suman los grados. Ejemplo:
(3xyz).(4x^2y^3)= 12x^3y^4z

Multiplicación de un polinomio y un monomio

Se multiplica cada término del polinomio por el monomio. Ejemplos:
a (b+c) = ab + ac \,\!
3 bx (2a+b) = 6abx + 3b^2x \,\!

Multiplicación de dos polinomios

En resumen, se puede concluir con esta regla:
  1. Se multiplica cada término del primer polinomio por cada término del segundo.
  2. Se reducen los términos semejantes.
Así:
(-3a) \cdot (-2b) = 6ab \,\!
(-3a) \cdot (2b) = (-6ab) \,\!

Producto de números complejos

El producto de dos números complejos puede calcularse mediante la siguiente fórmula:
(a+bi)(c+di) = (ac - bd) + i (bc + ad) \,\!

Multiplicación de números grandes

Existen diversos algoritmos que permiten multiplicar números grandes. El más rápido para los enteros que se manejan usualmente es el de Schönhage-Strassen.

Multiplicación de números enteros. - ...................................................:http://www.uv.es/varnau/AEC_513.pdf


Publicado por en

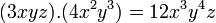
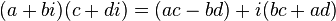
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)