Algoritmos cuánticos
algoritmo de Shor es un algoritmo cuántico para descomponer en factores un número N en tiempo O((log N)3) y espacio O(logN), así nombrado por Peter Shor.
Muchas criptografías de clave pública, tales como RSA, llegarían a ser obsoletas si el algoritmo de Shor es implementado alguna vez en una computadora cuánticapráctica. Un mensaje cifrado con RSA puede ser descifrado descomponiendo en factores la llave pública N, que es el producto de dos números primos. Los algoritmos clásicos conocidos no pueden hacer esto en tiempo O((log N)k) para ningún k, así que llegan a ser rápidamente poco prácticos a medida que se aumenta N. Por el contrario, el algoritmo de Shor puede romper RSA en tiempo polinómico. También se ha ampliado para atacar muchas otras criptografías públicas.
Como todos los algoritmos de computación cuántica, el algoritmo de Shor es probabilístico: da la respuesta correcta con alta probabilidad, y la probabilidad de fallo puede ser disminuida repitiendo el algoritmo.
El algoritmo de Shor fue demostrado en 2001 por un grupo en IBM, que descompuso 15 en sus factores 3 y 5, usando una computadora cuántica con 7 qubits.
Procedimiento
El problema que intenta solucionar el algoritmo de Shor es que, dado un número entero N, intentamos encontrar otro número entero p entre 1 y N que divida N.
El algoritmo de Shor consiste en dos partes:
- Una reducción del problema de descomponer en factores al problema de encontrar el orden, que se puede hacer en una computadora clásica.
- Un algoritmo cuántico para solucionar el problema de encontrar el periodo.
Parte clásica
- Escoja un número pseudo-aleatorio a < N
- Compute el mcd(a, N). Esto se puede hacer usando el algoritmo de Euclides.
-
- Si el mcd(a, N) ≠ 1, entonces es un factor no trivial de N, así que terminamos.
-
- Si no, utilice el subprograma para encontrar el período (ver abajo) para encontrar r, el período de la función siguiente:
 ,
,- es decir el número entero más pequeño r para el cual
 .
.
- Si r es impar, vaya de nuevo al paso 1.
- Si ar/2 ≡ -1 (mod N), vaya de nuevo al paso 1.
- Los factores de N son el mcd(ar/2 ± 1, N). Terminamos.
Parte cuántica: subprograma para encontrar el período
- Comience con un par de registros qubits de entrada y salida con log2N qubits cada uno, e inicialícelos a

- donde x va de 0 a N - 1.
- Construya f(x) como función cuántica y aplíquela al estado antedicho, para obtener
- Aplique la transformada de Fourier cuántica al registro de entrada. La transformada de Fourier cuántica en N puntos se define como:

- Lo que nos deja en el estado siguiente:
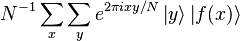
- Realice una medición. Obtenemos un cierto resultado y en el registro de entrada y f(x0) en el registro de salida. Puesto que f es periódica, la probabilidad de medir cierto y viene dada por

- El análisis muestra ahora que cuanto más alta es esta probabilidad, tanto más el yr/N es cercano a un número entero.
- Convierta a y/N en una fracción irreducible, y extraiga el denominador r ', que es un candidato a r.
- Compruebe si f(x) = f(x + r '). Si es así terminamos.
- Si no, obtenga más candidatos a r usando valores cercanos a y, o múltiplos de r '. Si cualquier candidato cumple las condiciones, terminamos.
- Si no, vaya de nuevo al paso 1 del subprograma.
Explicación del algoritmo
El algoritmo se compone de dos partes. La primera parte del algoritmo convierte el problema de descomponer en factores en el problema de encontrar el período de una función, y se puede implentar clásicamente. La segunda parte encuentra el período usando la transformada de Fourier cuántica, y es responsable de la aceleración cuántica.
I. Obtención de factores a partir del período
Los números enteros menores que N y coprimos con N forman un grupo finito bajo multiplicación módulo N, que se denota típicamente (Z/N Z)×. Para el final del paso 3, tenemos un número entero a en este grupo. Puesto que el grupo es finito, a debe tener un orden finito r, el número entero positivo más pequeño tal que
Por lo tanto, N |(ar - 1). Suponga que podemos obtener r, y es par. Entonces
r es el número entero positivo más pequeño tal que a r ≡ 1, así que N no puede dividir a (a r/2 - 1). Si N tampoco divide (ar/2 + 1), entonces N debe tener un factor común no trivial con (ar/2 - 1) y (a r/2 + 1).
Prueba: Por simplicidad, denote (ar/2 - 1) y (ar/2 + 1) u y v respectivamente. N | uv, luego kN = uv para un cierto número entero k. Suponga que el mcd(u, N) = 1; entonces mu + nN = 1 para ciertos números enteros m y n (ésta es una propiedad del máximo común divisor.) Multiplicando ambos lados por v, encontramos que mkN +nvN = v, luego N |v. Por contradicción, mcd(u, N) ≠ 1. Por un argumento similar, mcd(v, N) ≠ 1.
Esto nos provee de una factorización de N. Si N es el producto de dos primos, esta es la única factorización posible.
II. Encontrar el período
El algoritmo, para encontrar el período de Shor, se basa radicalmente en la capacidad de una computadora cuántica de estar en muchos estados simultáneamente. Los físicos llaman a este comportamiento superposición cuántica. Para computar el período de una función f, evaluamos la función en todos los puntos simultáneamente.
Sin embargo, la física cuántica no permite que tengamos acceso a toda esta información directamente. Una medición cuántica dará solamente uno de todos los valores posibles, destruyendo todos los otros. Por lo tanto tenemos que transformar cuidadosamente la superposición a otro estado que devuelva la respuesta correcta con alta probabilidad. Esto es alcanzado usando la transformada de Fourier cuántica.
Shor tuvo que solucionar así tres "problemas de implementación". Todos tuvieron que ser implementados "rápidos", que significa ejecutar con un número de puertas cuánticas que es polinómico en logN.
- Crear una superposición de estados. Esto puede hacerse aplicando las puertas de Hadamard a todos los qubits en el registro de entrada. Otro enfoque sería utilizar la transformada de Fourier cuántica (véase abajo).
- Implementar la función f como una transformada cuántica. Para alcanzar esto, Shor utilizó exponenciación por cuadrados para su transformación modular de la exponenciación.
- Realizar una transformada de Fourier cuántica. Usando puertas controladas NOT y puertas de una sola rotación de qubit, Shor diseñó un circuito para la transformada de Fourier cuántica que usa exactamente ((logN)2) puertas.
Después de todas estas transformaciones una medición dará una aproximación al período r. Por simplicidad asuma que hay una y tal que yr/N es un número entero. Entonces la probabilidad de medir y es 1. Para ver esto notemos que
para todos los números enteros b. Por lo tanto la suma que nos da la probabilidad de la medición y será N/r puesto que b toma aproximadamente N/r valores y así la probabilidad es 1/r. Hay r, y tales que yr/N es un número entero, luego la suma de las probabilidades es 1. Nota: otra manera de explicar el algoritmo de Shor es observando que es precisamente el algoritmo de valoración de fase cuántica disfrazado.
El paradigma de los algoritmos cuánticos es el algoritmo de Shor para factorizar números enteros. Para reducir el número de cubits necesarios se puede utilizar un truco llamado “precompilación” basado en conocer a priori los factores del número. Gracias a esta técnica, usando dos cubits en una implementación semiclásica, se han factorizado el número RSA-768 (de 768 bits) y el llamado N-20000 (de 20.000 bits). Sin el truco de la precompilación del algoritmo de Shor hubieran sido necesarios 1.154 cubits y 30.002 cubits, resp. Dicho truco no es aplicable cuando no se conocen los factores del número por lo que no puede utilizarse en criptoanálisis de claves públicas. Además, dicho truco puede utilizarse incluso en una implementación clásica del algoritmo de Shor utilizando números aleatorios generados tirando monedas (que salga cara H o cruz T); el nuevo récord se ha obtenido usando dicho truco. Pero lo importante a destacar es que, hasta el momento, el algoritmo de Shor nunca ha sido implementado en un ordenador cuántico de forma completa (sin “precompilación”). El artículo técnico es John A. Smolin, Graeme Smith, Alexander Vargo, “Oversimplifying quantum factoring,” Nature 499: 163–165, 11 Jul 2013. Este artículo me viene ni que pintado porque el viernes 12 de julio imparto el curso “Presente y futuro de la computación cuántica” en un curso de verano “Alan M. Turing: Enigmático, visionario y condenado,” coordinado por Ernesto Pimentel, director de la E.T.S.I. Informática de la Universidad de Málaga, que se imparte en Veléz Málaga.
Te recuerdo. El algoritmo cuántico de Shor para factorizar el número N=pq calcula sus dos factores p y q utilizando O(log N) cubits (el algoritmo original usa 3 log N cubits, pero hay versiones posteriores con sólo 2+(3/2) log N cubits, aunque la adición de algoritmos de corrección de errores requiere muchos más) y un tiempo de cálculo de O((log N)3), donde log N es el número de dígitos de N. El mejor algoritmo clásico requiere un coste exponencial en el número de dígitos. En 2001 (Nature) se factorizó el número 15 utilizando 7 cubits en lugar de 8; en 2009 (Science) se utilizaron 5 cubits, en 2007 (PRL,PRL) fueron 4 cubits y en 2012 (Nat.Phys.) sólo 3 cubits. El récord se obtuvo en 2012 (Nat.Phot. cuyo primer autor es el español Enrique Martín-López) con la factorización del número 21 utilizando 1+log 3 cubits en lugar de 10 cubits (en realidad son dos cubits, pero uno se usa siempre y el otro sólo en ciertos pasos del algoritmo, de ahí el valor log 3). El truco que se utiliza para reducir el número de cubits es “precompilar” el algoritmo en el “cableado” de la implementación (ya que se conocen los factores), lo que permite reducir el número de cubits hasta solamente 1 cubit.
algoritmo cuántico para sistemas de ecuaciones lineales, diseñado por Aram Harrow, Avinatan Hassidim, y Seth Lloyd es un algoritmo cuántico para resolver sistemas de ecuaciones lineales formulado en 2009. El algoritmo estima el resultado de una medida sobre el vector solución de un sistema de ecuaciones lineales dado.1
Es uno de los algoritmos fundamentales que junto con el algoritmo de Shor, el algoritmo de Grover y el algoritmo de simulación cuántica de Feynman esperan proporcionar un aumento de la velocidad exponencial respecto de sus versiones clásicas. Dado un sistema lineal disperso con un número de condición k, bajo y estando el usuario interesado en una medida sobre el vector solución, en vez del propio vector solución, el algoritmo tiene un tiempo de ejecución de O(log Nk2). Esto ofrece un aumento exponencial de la velocidad respecto al algoritmo clásico más rápido, cuyo tiempo de ejecución es O(N√k), donde N es el número de variables del sistema lineal.
Una implementación del algoritmo fue realizada en paralelo por primera vez en 2013 por Cai et al., Barz et al. y Pan et al. La demostración consistió en la resolución de un sistema simple de ecuaciones lineales especialmente diseñado para dispositivos cuánticos.2 3 4
Debido al uso de los sistemas lineales en prácticamente todas las áreas de la ciencia y la ingeniería, el algoritmo cuántico para sistemas de ecuaciones lineales tiene el potencial de ser el algoritmo cuántico más utilizado hasta ahora. Este es un importante hito para la computación cuántica ya que los anteriores algoritmos ofrecen una aceleración exponencial pero no tienen ni versatilidad ni obvias aplicaciones en el mundo real.
Procedimiento
El problema que estamos tratando de resolver es el siguiente: dada una matriz  Hermítica
Hermítica 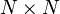 y un vector
y un vector 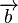 , encontrar el vector solución
, encontrar el vector solución 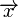 que satisfaga
que satisfaga  . Este algoritmo asume que el usuario no está interesado en los valores de
. Este algoritmo asume que el usuario no está interesado en los valores de 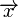 en si mismos, sino más bien en el resultado de aplicar algún operador
en si mismos, sino más bien en el resultado de aplicar algún operador  sobre
sobre  ,
,  .
.
 Hermítica
Hermítica 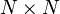 y un vector
y un vector 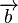 , encontrar el vector solución
, encontrar el vector solución 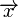 que satisfaga
que satisfaga  . Este algoritmo asume que el usuario no está interesado en los valores de
. Este algoritmo asume que el usuario no está interesado en los valores de 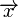 en si mismos, sino más bien en el resultado de aplicar algún operador
en si mismos, sino más bien en el resultado de aplicar algún operador  sobre
sobre  ,
,  .
.
Primero, el algoritmo representa el vector 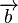 como un estado cuántico de la forma:
como un estado cuántico de la forma:
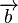 como un estado cuántico de la forma:
como un estado cuántico de la forma:
Después utilizamos técnicas de simulación de hamiltonianos para aplicar el operador unitario  a
a  para una superposición de diferentes tiempos
para una superposición de diferentes tiempos  . Las operaciones de descomposición de
. Las operaciones de descomposición de  en la eigenbase de
en la eigenbase de  y de encontrar los correspondientes eigenvalores
y de encontrar los correspondientes eigenvalores 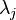 , son facilitadas por el uso del algoritmo cuántico de estimación de fase.
, son facilitadas por el uso del algoritmo cuántico de estimación de fase.
 a
a  para una superposición de diferentes tiempos
para una superposición de diferentes tiempos  . Las operaciones de descomposición de
. Las operaciones de descomposición de  en la eigenbase de
en la eigenbase de  y de encontrar los correspondientes eigenvalores
y de encontrar los correspondientes eigenvalores 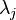 , son facilitadas por el uso del algoritmo cuántico de estimación de fase.
, son facilitadas por el uso del algoritmo cuántico de estimación de fase.
El estado del sistema después de esta descomposición es aproximadamente.
Donde  es el eigenvector de la base
es el eigenvector de la base  , y
, y 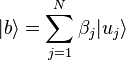
 es el eigenvector de la base
es el eigenvector de la base  , y
, y 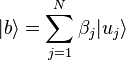
Nos gustaría realizar una aplicación lineal de  a
a  , donde
, donde  es una constante de normalización. La operación no es unitaria y por tanto requerimos un número de repeticiones debido a que tiene una probabilidad de error. Después de tener éxito, calculamos el registro
es una constante de normalización. La operación no es unitaria y por tanto requerimos un número de repeticiones debido a que tiene una probabilidad de error. Después de tener éxito, calculamos el registro  y es inversamente proporcional al estado:
y es inversamente proporcional al estado:
 a
a  , donde
, donde  es una constante de normalización. La operación no es unitaria y por tanto requerimos un número de repeticiones debido a que tiene una probabilidad de error. Después de tener éxito, calculamos el registro
es una constante de normalización. La operación no es unitaria y por tanto requerimos un número de repeticiones debido a que tiene una probabilidad de error. Después de tener éxito, calculamos el registro  y es inversamente proporcional al estado:
y es inversamente proporcional al estado:
Donde 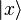 es la representación cuántica del vector solución x deseado. Para obtener todas las componentes de x deberíamos repetir el procedimiento al menos N veces. Sin embargo, es frecuente el caso de que no interese x en sí mismo, sino más bien el valor esperado de un operador lineal Mactuando sobre x Gracias al mapeo de M al operador cuántico y realizando la medida cuántica correspondiente a M, obtenemos un valor esperado estimado
es la representación cuántica del vector solución x deseado. Para obtener todas las componentes de x deberíamos repetir el procedimiento al menos N veces. Sin embargo, es frecuente el caso de que no interese x en sí mismo, sino más bien el valor esperado de un operador lineal Mactuando sobre x Gracias al mapeo de M al operador cuántico y realizando la medida cuántica correspondiente a M, obtenemos un valor esperado estimado  .. Esto permite extraer una amplia variedad de características del vector x incluyendo la normalización, los pesos en las diferentes partes del espacio de estado, y los momentos, sin calcular realmente todos los valores de la solución x.
.. Esto permite extraer una amplia variedad de características del vector x incluyendo la normalización, los pesos en las diferentes partes del espacio de estado, y los momentos, sin calcular realmente todos los valores de la solución x.
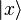 es la representación cuántica del vector solución x deseado. Para obtener todas las componentes de x deberíamos repetir el procedimiento al menos N veces. Sin embargo, es frecuente el caso de que no interese x en sí mismo, sino más bien el valor esperado de un operador lineal Mactuando sobre x Gracias al mapeo de M al operador cuántico y realizando la medida cuántica correspondiente a M, obtenemos un valor esperado estimado
es la representación cuántica del vector solución x deseado. Para obtener todas las componentes de x deberíamos repetir el procedimiento al menos N veces. Sin embargo, es frecuente el caso de que no interese x en sí mismo, sino más bien el valor esperado de un operador lineal Mactuando sobre x Gracias al mapeo de M al operador cuántico y realizando la medida cuántica correspondiente a M, obtenemos un valor esperado estimado  .. Esto permite extraer una amplia variedad de características del vector x incluyendo la normalización, los pesos en las diferentes partes del espacio de estado, y los momentos, sin calcular realmente todos los valores de la solución x.
.. Esto permite extraer una amplia variedad de características del vector x incluyendo la normalización, los pesos en las diferentes partes del espacio de estado, y los momentos, sin calcular realmente todos los valores de la solución x.Explicación del algoritmo
Inicialización
Primero, el algoritmo requiere que la matriz  sea hermitica de forma que podamos convertirla en un operador unitario. En el caso de que A no sea hermítica, definimos:
sea hermitica de forma que podamos convertirla en un operador unitario. En el caso de que A no sea hermítica, definimos:
 sea hermitica de forma que podamos convertirla en un operador unitario. En el caso de que A no sea hermítica, definimos:
sea hermitica de forma que podamos convertirla en un operador unitario. En el caso de que A no sea hermítica, definimos:
Como  es Hermitica, el algoritmo puede ahora ser usado para resolver
es Hermitica, el algoritmo puede ahora ser usado para resolver  para obtener
para obtener  .
.
 es Hermitica, el algoritmo puede ahora ser usado para resolver
es Hermitica, el algoritmo puede ahora ser usado para resolver  para obtener
para obtener  .
.
Segundo, el algoritmo requiere un procedimiento eficiente para preparar  , la representación cuántica de b. Se asume que existe un operador lineal
, la representación cuántica de b. Se asume que existe un operador lineal  que puede tomar eficientemente algún estado arbitrario
que puede tomar eficientemente algún estado arbitrario  de
de  o que este algoritmo es una subrutina de un algoritmo más grande y este
o que este algoritmo es una subrutina de un algoritmo más grande y este  es tomado como una entrada. Cualquier error en la preparación del estado
es tomado como una entrada. Cualquier error en la preparación del estado  es ignorado.
es ignorado.
 , la representación cuántica de b. Se asume que existe un operador lineal
, la representación cuántica de b. Se asume que existe un operador lineal  que puede tomar eficientemente algún estado arbitrario
que puede tomar eficientemente algún estado arbitrario  de
de  o que este algoritmo es una subrutina de un algoritmo más grande y este
o que este algoritmo es una subrutina de un algoritmo más grande y este  es tomado como una entrada. Cualquier error en la preparación del estado
es tomado como una entrada. Cualquier error en la preparación del estado  es ignorado.
es ignorado.
Finalmente, el algoritmo asume que el estado 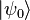 puede ser preparado eficientemente. Donde
puede ser preparado eficientemente. Donde
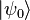 puede ser preparado eficientemente. Donde
puede ser preparado eficientemente. Donde
para algún  grande. Los coeficientes de
grande. Los coeficientes de 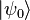 son escogidos para minimizar la pérdida de una cierta función cuadrática que induce error en la subrutina
son escogidos para minimizar la pérdida de una cierta función cuadrática que induce error en la subrutina  que se describe a continuación.
que se describe a continuación.
 grande. Los coeficientes de
grande. Los coeficientes de 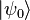 son escogidos para minimizar la pérdida de una cierta función cuadrática que induce error en la subrutina
son escogidos para minimizar la pérdida de una cierta función cuadrática que induce error en la subrutina  que se describe a continuación.
que se describe a continuación.Estimación de la fase
La estimación de la fase es usada para transformar la matriz Hermítica  en un operador unitario, el cual pueda ser aplicado en el futuro. Esto es posible si A es s-sparse y eficientemente fila computable, lo que significa que tiene al menos s entradas no nulas por fila y dado un índice de fila estas entradas pueden ser calculadas en un tiempo del orden O(s). Bajo estas suposiciones, la estimación de fase produce
en un operador unitario, el cual pueda ser aplicado en el futuro. Esto es posible si A es s-sparse y eficientemente fila computable, lo que significa que tiene al menos s entradas no nulas por fila y dado un índice de fila estas entradas pueden ser calculadas en un tiempo del orden O(s). Bajo estas suposiciones, la estimación de fase produce 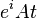 para ser simulada en un tiempo
para ser simulada en un tiempo  .
.
 en un operador unitario, el cual pueda ser aplicado en el futuro. Esto es posible si A es s-sparse y eficientemente fila computable, lo que significa que tiene al menos s entradas no nulas por fila y dado un índice de fila estas entradas pueden ser calculadas en un tiempo del orden O(s). Bajo estas suposiciones, la estimación de fase produce
en un operador unitario, el cual pueda ser aplicado en el futuro. Esto es posible si A es s-sparse y eficientemente fila computable, lo que significa que tiene al menos s entradas no nulas por fila y dado un índice de fila estas entradas pueden ser calculadas en un tiempo del orden O(s). Bajo estas suposiciones, la estimación de fase produce 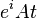 para ser simulada en un tiempo
para ser simulada en un tiempo  .
.Subrutina de inversión de U
La subrutina clave del algoritmo, denotada por  es definida como:
es definida como:
 es definida como:
es definida como:
1. Preparar  sobre el registro C
sobre el registro C
 sobre el registro C
sobre el registro C
2. Aplicar la evolución condicional Hamiltoniana (suma)
3. Aplicar la transformada de Furier al registro C. Marcamos los estados base resultantes con 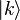 para
para  := 0, ..., T − 1. Definiendo
:= 0, ..., T − 1. Definiendo  .
.
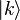 para
para  := 0, ..., T − 1. Definiendo
:= 0, ..., T − 1. Definiendo  .
.
4. Unir un registro tri-dimensional S al estado
5. Invertimos los pasos 1-3, sin calcular cualquier basura producida en el camino.
Donde las funciones f y g son funciones de filtro. Los estados 'nada', 'bien', y 'mal' son usados para indicar al cuerpo del bucle como proceder, 'nada' indica que la inversión de la matriz deseada todavía no se ha producido, 'bien' indica que la inversión ha tenido lugar, y 'mal' indica que parte de  está en el subespacio de A mal acondicionada y que el algoritmo no será capaz de producir la inversión deseada.
está en el subespacio de A mal acondicionada y que el algoritmo no será capaz de producir la inversión deseada.
 está en el subespacio de A mal acondicionada y que el algoritmo no será capaz de producir la inversión deseada.
está en el subespacio de A mal acondicionada y que el algoritmo no será capaz de producir la inversión deseada.Lazo principal
El cuerpo del algoritmo sigue el procedimiento de amplificación de la amplitud: empezando con  , se repiten las siguientes operaciones:
, se repiten las siguientes operaciones:
 , se repiten las siguientes operaciones:
, se repiten las siguientes operaciones:
donde
y
Después de cada repetición,  es medido y producirá un valor de 'nada', 'bien', o 'mal' como se describió anteriormente. Este bucle es repetido hasta que
es medido y producirá un valor de 'nada', 'bien', o 'mal' como se describió anteriormente. Este bucle es repetido hasta que  es medido 'bien', lo cual ocurre con una probabilidad
es medido 'bien', lo cual ocurre con una probabilidad  . En lugar de repetir
. En lugar de repetir  veces para minimizar el error, se utiliza la amplificación de amplitud para lograr la misma capacidad de recuperación de error usando sólo
veces para minimizar el error, se utiliza la amplificación de amplitud para lograr la misma capacidad de recuperación de error usando sólo  repeticiones.
repeticiones.
 es medido y producirá un valor de 'nada', 'bien', o 'mal' como se describió anteriormente. Este bucle es repetido hasta que
es medido y producirá un valor de 'nada', 'bien', o 'mal' como se describió anteriormente. Este bucle es repetido hasta que  es medido 'bien', lo cual ocurre con una probabilidad
es medido 'bien', lo cual ocurre con una probabilidad  . En lugar de repetir
. En lugar de repetir  veces para minimizar el error, se utiliza la amplificación de amplitud para lograr la misma capacidad de recuperación de error usando sólo
veces para minimizar el error, se utiliza la amplificación de amplitud para lograr la misma capacidad de recuperación de error usando sólo  repeticiones.
repeticiones.Media escalar
Después de medir satisfactoriamente 'bien' en el sistema S el sistema estará en un estado proporcional a:
Finalmente, realizamos la operación correspondiente a M y obtenemos una estimación del valor de  .
.
 .
.Análisis del tiempo de ejecución
Eficiencia clásica
El mejor algoritmo clásico que produce actualmente la solución 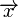 es la eliminación Gaussiana, la cual corre en un tiempo de
es la eliminación Gaussiana, la cual corre en un tiempo de 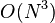 .
.
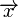 es la eliminación Gaussiana, la cual corre en un tiempo de
es la eliminación Gaussiana, la cual corre en un tiempo de 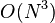 .
.
Si A es s-sparse, donde s es significativamente más pequeño que N, entonces el método del gradiente conjugado puede ser usado para encontrar el vector solución 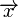 en tiempo
en tiempo  minimizando la función cuadrática
minimizando la función cuadrática  .
.
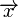 en tiempo
en tiempo  minimizando la función cuadrática
minimizando la función cuadrática  .
.
Cuando solo se necesita un resumen estadístico del vector solución 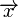 , como en el caso del algorimo cuantico para sistemas de ecuaciones lineales, un cálculo clásico puede encontrar una estimación de
, como en el caso del algorimo cuantico para sistemas de ecuaciones lineales, un cálculo clásico puede encontrar una estimación de  en
en  .
.
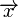 , como en el caso del algorimo cuantico para sistemas de ecuaciones lineales, un cálculo clásico puede encontrar una estimación de
, como en el caso del algorimo cuantico para sistemas de ecuaciones lineales, un cálculo clásico puede encontrar una estimación de  en
en  .
.Eficiencia cuántica
El algoritmo cuantico para resolver el sistema de ecuaciones originalmente propuesto por Harrow et al. demostró ser del orden 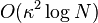 . El tiempo de ejecución de este algoritmo mejorado por Andris Ambainis se incrementó a
. El tiempo de ejecución de este algoritmo mejorado por Andris Ambainis se incrementó a 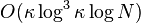 .6
.6
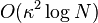 . El tiempo de ejecución de este algoritmo mejorado por Andris Ambainis se incrementó a
. El tiempo de ejecución de este algoritmo mejorado por Andris Ambainis se incrementó a 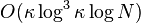 .6
.6Optimización
Un importante factor en la realización del algoritmo de inversión es el número de condición  , el cual representa el ratio del mayor y el menor eigenvalor de
, el cual representa el ratio del mayor y el menor eigenvalor de  . A medida que el número de condición aumenta, la facilidad con la que el vector solución puede ser encontrada usando los métodos del gradiente descendente tales como el método del gradiente conjugado descendente, la matriz
. A medida que el número de condición aumenta, la facilidad con la que el vector solución puede ser encontrada usando los métodos del gradiente descendente tales como el método del gradiente conjugado descendente, la matriz  está más cerca de una matriz que no puede ser invertida y el vector solución se convierte en menos estable. Este algoritmo asume que todos los elementos de la matriz
está más cerca de una matriz que no puede ser invertida y el vector solución se convierte en menos estable. Este algoritmo asume que todos los elementos de la matriz  se encuentran entre
se encuentran entre  y 1, en cuyo caso se logra un tiempo de ejecución proporcional a
y 1, en cuyo caso se logra un tiempo de ejecución proporcional a  . Por tanto, el incremento de velocidad sobre los algoritmos clásicos se ve incrementado cuando
. Por tanto, el incremento de velocidad sobre los algoritmos clásicos se ve incrementado cuando  es un
es un 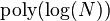 .1
.1
 , el cual representa el ratio del mayor y el menor eigenvalor de
, el cual representa el ratio del mayor y el menor eigenvalor de  . A medida que el número de condición aumenta, la facilidad con la que el vector solución puede ser encontrada usando los métodos del gradiente descendente tales como el método del gradiente conjugado descendente, la matriz
. A medida que el número de condición aumenta, la facilidad con la que el vector solución puede ser encontrada usando los métodos del gradiente descendente tales como el método del gradiente conjugado descendente, la matriz  está más cerca de una matriz que no puede ser invertida y el vector solución se convierte en menos estable. Este algoritmo asume que todos los elementos de la matriz
está más cerca de una matriz que no puede ser invertida y el vector solución se convierte en menos estable. Este algoritmo asume que todos los elementos de la matriz  se encuentran entre
se encuentran entre  y 1, en cuyo caso se logra un tiempo de ejecución proporcional a
y 1, en cuyo caso se logra un tiempo de ejecución proporcional a  . Por tanto, el incremento de velocidad sobre los algoritmos clásicos se ve incrementado cuando
. Por tanto, el incremento de velocidad sobre los algoritmos clásicos se ve incrementado cuando  es un
es un 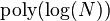 .1
.1
Si el tiempo de ejecución del algoritmo fuera polilogarítmico en  entonces los problemas que tienen solución sobre n qubits podrían resolverse en tiempo poly(n). Haciendo que la fase de complejidad BQP sea igual a PSPACE.1
entonces los problemas que tienen solución sobre n qubits podrían resolverse en tiempo poly(n). Haciendo que la fase de complejidad BQP sea igual a PSPACE.1
 entonces los problemas que tienen solución sobre n qubits podrían resolverse en tiempo poly(n). Haciendo que la fase de complejidad BQP sea igual a PSPACE.1
entonces los problemas que tienen solución sobre n qubits podrían resolverse en tiempo poly(n). Haciendo que la fase de complejidad BQP sea igual a PSPACE.1Análisis del error
La realización de la estimación de fase, que es la fuente dominante de error, se hace simulando  . Asumiendo que
. Asumiendo que  es s-dispersa, esta puede ser realizada con un error acotado por la constante
es s-dispersa, esta puede ser realizada con un error acotado por la constante  , la cual que se traducirá en el error aditivo logrado en el estado de salida
, la cual que se traducirá en el error aditivo logrado en el estado de salida 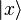 .
.
 . Asumiendo que
. Asumiendo que  es s-dispersa, esta puede ser realizada con un error acotado por la constante
es s-dispersa, esta puede ser realizada con un error acotado por la constante  , la cual que se traducirá en el error aditivo logrado en el estado de salida
, la cual que se traducirá en el error aditivo logrado en el estado de salida 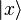 .
.
El paso de estimación de fase falla del  en la estimación de
en la estimación de , lo cual se traslada dentro del error relativo a
, lo cual se traslada dentro del error relativo a 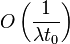 como
como  . Si
. Si  , tomando
, tomando  , induce un error final
, induce un error final  . Esto requiere que el tiempo total de ejecución sea incrementado proporcionalmente a
. Esto requiere que el tiempo total de ejecución sea incrementado proporcionalmente a 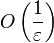 para minimizar el error.
para minimizar el error.
 en la estimación de
en la estimación de , lo cual se traslada dentro del error relativo a
, lo cual se traslada dentro del error relativo a 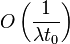 como
como  . Si
. Si  , tomando
, tomando  , induce un error final
, induce un error final  . Esto requiere que el tiempo total de ejecución sea incrementado proporcionalmente a
. Esto requiere que el tiempo total de ejecución sea incrementado proporcionalmente a 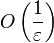 para minimizar el error.
para minimizar el error.Realización experimental
Si bien aún no existe un ordenador cuántico que realmente pueda ofrecer un aumento de velocidad sobre la computadora clásica, la implementación de una "prueba de concepto" sigue siendo un hito importante en el desarrollo de un nuevo algoritmo cuántico. Demostrar el algoritmo cuántico para sistemas de ecuaciones lineales seguía siendo un desafío en los años posteriores a su propuesta hasta que en el año 2013 fue demostrado por Cai et al., Barz et al. y Pan et al. en paralelo.
Cai et al.
Publicado en Physical Review Letters 110, 230501 (2013), Cai et al. informaron de una demostración experimental del ejemplo significativo más simple de este algoritmo, esto es, resolvieron un sistema de ecuaciones lineales 2*2 para varios vectores de entrada. El circuito cuántico está optimizado y compilado dentro de una red óptica lineal con cuatro bits fotónicos (qubits) y cuatro puertas lógicas controladas, las cuales son usadas para implementar coherentemente todas las subrutinas de este algoritmo. Para varios vectores de entrada, la computación cuántica da soluciones para las ecuaciones lineales con precisión razonablemente alta, que van desde fidelidades de 0.825 to 0.993.
Barz et al.
El 5 de Febrero, 2013 Barz et al. demostraron el algoritmo cuántico para un sistema lineal de ecuaciones sobre una arquitectura de computación cuántica fotónica. Esta implementación uso dos puertas entrelazadas consecutivas sobre el mismo par de qubits con codificación en la polarización. Se utilizaron dos puertas separadas NOT-controladas donde la operación exitosa de la primera era anunciada por una medida sobre dos fotones auxiliares. Barz et al. encontraron que la fidelidad en el estado de salida varió desde el 64.4% al 98.1% debido a la influencia de las emisiones de orden superior por conversión paramétrica descendente espontanea.3
Pan et al.
El 8 de febrero, 2013 Pan et al. informaron de una prueba experimental de concepto del algoritmo cuántico utilizando un procesador de información cuántica de resonancia magnética nuclear de 4 qubit. La aplicación fue probada usando sistemas lineales simples de sólo 2 variables. A través de tres experimentos obtuvieron el vector solución con más de 96% de fidelidad.4
Aplicaciones
Los ordenadores cuánticos son dispositivos que aprovechan la mecánica cuántica para realizar cálculos en formas que los ordenadores clásicos no pueden. Para ciertos problemas, los algoritmos cuánticos proporcionan aceleraciones exponenciales respecto a sus homólogos clásicos, el ejemplo más famoso es el algoritmo de factorización de Shor. Pocas de estas aceleraciones son conocidas, y las que lo son (como el uso de las computadoras cuánticas para simular otros sistemas cuánticos) han encontrado hasta ahora un uso limitado fuera del dominio de la mecánica cuántica. Este algoritmo proporciona un método exponencialmente rápido para estimar las características de la solución de un conjunto de ecuaciones lineal, el cual es un problema omnipresente en la ciencia de ingeniería, tanto en sí mismo como siendo una subrutina de problemas más complejos.
Resolución de ecuaciones diferenciales lineales
Domic Berry propuso un nuevo algoritmo para resolver ecuaciones diferenciales lineales dependientes del tiempo como una extensión del algoritmo cuántico para resolver sistemas de ecuaciones lineales. Berry proporciona un algoritmo eficiente para resolver la evolución a tiempo completo bajo ecuaciones diferenciales lineales dispersas sobre un ordenador cuántico.7
Mínimos cuadrados apropiados
Wiebe et al. proporcionan un nuevo algoritmo cuántico para determinar la calidad de los mínimos cuadrados de una función continua utilizada para aproximar un conjunto de puntos discretos, aplicando el algoritmo cuántico para sistemas de ecuaciones lineales. Al aumentar la cantidad de puntos discretos, el tiempo requerido para producir el ajuste de mínimos cuadrados usando incluso un ordenador cuántico que ejecuta un algoritmo cuántico de estado tomográfico se hace muy grande. Weibe et al. encontraron que en muchos casos, su algoritmo puede encontrar de una manera eficiente una concisa aproximación a los puntos dados, eliminando la necesidad del algoritmo tomográfico de mayor complejidad.8
Aprendizaje automático y análisis de Big Data
El aprendizaje automático es el estudio de los sistemas que pueden identificar tendencias en los datos. Las tareas del aprendizaje automático involucran frecuentemente manipulación y clasificación de grandes volúmenes de datos en espacios vectoriales de grandes dimensiones. El tiempo de ejecución de los algoritmos de aprendizaje automático clásicos está limitado por la dependencia polinómica de ambos, volumen de datos y dimensiones del espacio. Los computadores cuánticos son capaces de manipular vectores de grandes dimensiones usando el producto tensorial de espacios así pues son la plataforma perfecta para los algoritmos de aprendizaje automático.9
El algoritmo cuántico para sistemas de ecuaciones lineales se ha aplicado a una máquina de vectores soporte, la cual es una optimización lineal de la clasificación binaria no lineal. Una máquina de soporte vectorial se puede utilizar para el aprendizaje automático supervisado, en el cual se encuentra disponible un conjunto de datos de entrenamiento ya clasificado, o en el aprendizaje no supervisado, en el cual todos los datos del sistema están no clasificados. Rebentrost et al. demostraron que una máquina de vectores de soporte cuántica se puede utilizar en la clasificación de big data y lograr una aceleración exponencial con respecto a los ordenadores clásicos.
Los ordenadores cuánticos son capaces de hacer cosas maravillosas, y es una pena que no existan todavía. Sin embargo, los físicos y los matemáticos ya están desarrollando algoritmos que permitirán usar estos increíbles cacharros para resolver problemas que los ordenadores actuales no pueden ni siquiera encarar con posibilidades de éxito. Aram Harrow, Avinatan Hassidim y Seth Lloyd acaban de proponer un algoritmo cuántico capaz resolver un conjunto de ecuaciones lineales exponencialmente más rápido que cualquier algoritmo clásico.¿Deberemos aprender a programar nuevamente?
A pesar del incremento de potencia que cada año hace de nuestros ordenadores máquinas más poderosas, existen una serie de problemas que por su complejidad resultan imposibles de resolver mediante hardware y algoritmos “clásicos”. Los futuros ordenadores cuánticos, que utilizan las extrañas leyes de la física de partículas para realizar sus operaciones, no tienen prácticamente limitaciones, y se ha demostrado que algunos problemas -como la factorización de enteros sobre la que se basa casi toda la criptografía actual– pueden resolverse en un tiempo casi despreciable. Día a día los matemáticos y los físicos ponen a punto nuevos algoritmos especialmente concebidos para ser ejecutados sobre estos dispositivos, a pesar de que aún no sepamos cómo construirlos. En un artículo publicado recientemente en Physical Review Letters, Aram Harrow de la Universidad de Bristol (Reino Unido), junto Avinatan Hassidim y Seth Lloyd del MIT (EEUU), proponen un algoritmo cuántico capaz resolver un conjunto de ecuaciones lineales que es exponencialmente más rápido que cualquier algoritmo clásico.
Una ecuación de primer grado o ecuación lineal es un planteamiento de igualdad, involucrando una o más variables a la primera potencia, que no contiene productos entre las variables. Es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia. Son expresiones similares a la siguiente: 3x + 2y = 7. Representadas sobre un sistema de ejes cartesianos, estas ecuaciones se convierten en rectas. La ecuación anterior puede ser resuelta por cualquier estudiante, pero el problema se complica cuando forma parte de un sistema más grande, que contienemiles de millones de variables y miles de millones de ecuaciones. Tales sistemas no son son inusuales en las aplicaciones modernas, y resultan esenciales para elaborar simulaciones de las condiciones meteorológicas, las reacciones nucleares u otros fenómenos físicos. Los algoritmos más eficientes pueden resolver grandes sistemas "N x N" (sistemas con N ecuaciones lineales y N incógnitas) utilizando ordenadores convencionales. Sin embargo, el tiempo de cálculo necesario para llegar a la solución crece al menos tan rápido como N: si N se hace 1.000 veces más grande, el problema tomará -en el mejor de los casos- 1.000 veces más tiempo para ser resuelto. A menudo mucho más.
El algoritmo cuántico que proponen Harrow, Avinatan Hassidim y Lloyd es una especie de “atajo inteligente”. En efecto, su trabajo demuestra que un ordenador cuántico puede proporcionar soluciones relevantes sin necesidad de resolver la totalidad de las ecuaciones implicadas. Con este algoritmo (y un ordenador capaz de ejecutarlo) seríamos capaces de hacer predicciones meteorológicas que en lugar de referirse a una provincia o ciudad, se refieran a cada uno de los bloques de casas que la conforman. Al igual que otros algoritmos cuánticos, este codifica toda la información relevante sobre el sistema a resolver en “bits cuánticos” o qbits. A diferencia de los bits ordinarios, los bits cuánticos pueden poseer valores 0 y 1 al mismo tiempo. Para los físicos, esta especie de esquizofrenia informática se denomina “superposición de estados”. El algoritmo transforma los bits en un estado que codifica una superposición de todas las posibles soluciones del sistema, asignando todos los posibles valores a las variables de las ecuaciones. De esta “solución universal” se puede entonces extraer información relevante sobre las soluciones particulares sin necesidad de calcularlas completamente.
Dejando de lado la complejidad matemática del asunto, lo concreto es que el aumento de velocidad es enorme: el tiempo necesario para encontrar esta solución universal sólo crece con el número de dígitos de N. Así, si N se hace 1,000 veces más grande, el algoritmo demora solamente el triple de tiempo en encontrar la solución, ya que N -a pesar de ser 1,000 veces mayor- solo tiene tres veces más dígitos. Este tipo de algoritmo, como es de esperar, entusiasma a los científicos. En la década de 1990 se encontró uno similar capaz de factorizar grandes números primos de forma casi instantánea, que nos obligará a buscar nuevos sistemas de seguridad cuando seamos capaces de construir ordenadores cuánticos. Y ese día no está muy lejos.
Efectivamente, ya hemos sido capaces de construir ordenadores cuánticos experimentales, capaces de operar con unos pocos bits. Los científicos creen que fabricar un ordenador más poderoso será posible dentro de una o dos décadas. Cuando llegue ese día, algoritmos como este revolucionaran campos tan dispares como la bioestadística, la ecología, la ingeniería y -por supuesto- los videojuegos: todos dependen en gran medida en la resolución de ecuaciones lineales.



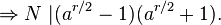


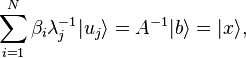




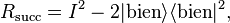


No hay comentarios:
Publicar un comentario