Termodinámica química es el estudio de la interrelación entre el calor y el trabajo con reacciones químicas o con cambios físicos del estado dentro de los confines de las leyes termodinámicas. La termodinámica química involucra no sólo mediciones de varias propiedades termodinámicas en el laboratorio, sino también la aplicación de métodos matemáticos al estudio de preguntas químicas y a las reacciones de los procesos.
La estructura de la química termodinámica está basada en las primeras dos leyes de la termodinámica. Comenzando a partir de la primera y segunda ley de la termodinámica, cuatro expresiones matemáticas llamadas "ecuaciones fundamentales de Gibbs" se pueden obtener. A partir de estas cuatro, gran cantidad de ecuaciones relacionadas con propiedades termodinámicas del sistema termodinámico pueden ser derivadas utilizando matemáticas relativamente sencillas. Esto delinea la infraestructura matemática de la termodinámica química.
Historia
En 1865, el físico alemán Rudolf Clausius en su Teoría Mecánica del Calor sugirió que los principios de la termoquímica, por ejemplo el calor producido en reacciones de combustión, podían ser aplicados a los principios de la termodinámica.2 Ampliando el trabajo de Clausius, entre los años 1873 y 1876 el físico-matemático americano Willard Gibbs publicó una serie de tres artículos, siendo el más famoso de ellos En el Equilibrio de Sustancias Heterogéneas. En estos artículos, Gibbs mostró cómo las primeras dosleyes de la termodinámica podían ser medidas de manera gráfica y matemática para determinar tanto el equilibrio termodinámico de las reacciones químicas como su respectiva tendencia a ocurrir o proceder. La colección de artículos de Gibbs proporcionó el primer cuerpo unificado de teoremas termodinámicos a partir de los principios desarrollados por otros, tales como Clausius y Sadi Carnot.
A inicios del siglo XX, dos grandes publicaciones aplicaron exitosamente en procesos químicos los principios desarrollados por Gibbs y fue así como se estableció el fundamento para la ciencia de la termodinámica química. La primera publicación fue el libro de texto de 1923 Termodinámica y la Energía Libre de las Sustancias Químicas por Gilbert N. Lewis y Merle Randall. Este libro fue responsable de reemplazar afinidad química por el término energía libre en el mundo del habla inglés. La segunda fue el libro de 1933 Termodinámica Moderna por los métodos de Willard Gibbs escrito por E. A. Guggenheim. En esta manera, Lewis, Randall y Guggenheim son considerados como los fundadores de la termodinámica química moderna debido a la gran contribución que generaron estos dos libros en unificar la aplicación de la termodinámica a la química.1
Resumen
El principal objetivo de la termodinámica química es la creación de un criterio para la determinación de la viabilidad o espontaneidad de una transformación dada.3 De esta manera, la termodinámica química es comúnmente utilizada para predecir los intercambios de energía que ocurren en los siguientes procesos:
- Reacciones químicas
- Cambios de fase
- La formación de soluciones
Las siguientes funciones de estado son la principal preocupación en la termodinámica química:
- Energía interna (U)
- Entalpía (H)
- Entropía (S)
- Energía libre de Gibbs (G)
Muchas identidades en la termodinámica química surgen de la aplicación de la primera y segunda leyes de la termodinámica, particularmente la ley de la conservación de energía a estas funciones de estado.
Las 3 leyes de la termodinámica:
- La energía del universo es constante.
- En cualquier proceso espontáneo siempre hay un incremento de la entropía en el universo.
- La entropía de un cristal perfecto en el 0 kelvin es cero.
Energía química
Energía química es el potencial de una sustancia química para experimentar una transformación a través de una reacción química o para transformar otras sustancias químicas. Romper o generar enlaces químicos implica energía, la cual puede ser absorbida o generada de un sistema químico.
La energía que puede ser liberada (o absorbida) debido a una reacción entre un conjunto de sustancias químicas es igual a la diferencia entre el contenido energético en los productos y reactivos. Este cambio en la energía es llamado el cambio en la energía interna de una reacción química. Donde  es la energía interna de la formación de moléculas de reactivos que puede ser calculado a partir de las energías de enlace de varios enlaces químicos de las moléculas bajo consideración y
es la energía interna de la formación de moléculas de reactivos que puede ser calculado a partir de las energías de enlace de varios enlaces químicos de las moléculas bajo consideración y  es la energía interna de la formación de las moléculas de producto. El cambio en la energía interna de un proceso es igual al cambio de calor si es medido bajo condiciones de volumen constante, así como en un contenedor rígido tal como una bomba calorimétrica. Sin embargo, bajo condiciones de presión constante, como reacciones en recipientes abiertos a la atmósfera, el cambio de calor medido no siempre es igual al cambio de energía interna, ya que el trabajo presión-volumen también libera o absorbe energía. (El cambio de calor a presión constante es llamado cambio de entalpía; para este caso la entalpía de formación).
es la energía interna de la formación de las moléculas de producto. El cambio en la energía interna de un proceso es igual al cambio de calor si es medido bajo condiciones de volumen constante, así como en un contenedor rígido tal como una bomba calorimétrica. Sin embargo, bajo condiciones de presión constante, como reacciones en recipientes abiertos a la atmósfera, el cambio de calor medido no siempre es igual al cambio de energía interna, ya que el trabajo presión-volumen también libera o absorbe energía. (El cambio de calor a presión constante es llamado cambio de entalpía; para este caso la entalpía de formación).
 es la energía interna de la formación de moléculas de reactivos que puede ser calculado a partir de las energías de enlace de varios enlaces químicos de las moléculas bajo consideración y
es la energía interna de la formación de moléculas de reactivos que puede ser calculado a partir de las energías de enlace de varios enlaces químicos de las moléculas bajo consideración y  es la energía interna de la formación de las moléculas de producto. El cambio en la energía interna de un proceso es igual al cambio de calor si es medido bajo condiciones de volumen constante, así como en un contenedor rígido tal como una bomba calorimétrica. Sin embargo, bajo condiciones de presión constante, como reacciones en recipientes abiertos a la atmósfera, el cambio de calor medido no siempre es igual al cambio de energía interna, ya que el trabajo presión-volumen también libera o absorbe energía. (El cambio de calor a presión constante es llamado cambio de entalpía; para este caso la entalpía de formación).
es la energía interna de la formación de las moléculas de producto. El cambio en la energía interna de un proceso es igual al cambio de calor si es medido bajo condiciones de volumen constante, así como en un contenedor rígido tal como una bomba calorimétrica. Sin embargo, bajo condiciones de presión constante, como reacciones en recipientes abiertos a la atmósfera, el cambio de calor medido no siempre es igual al cambio de energía interna, ya que el trabajo presión-volumen también libera o absorbe energía. (El cambio de calor a presión constante es llamado cambio de entalpía; para este caso la entalpía de formación).
Otro término útil es el calor de combustión, el cual es la energía liberada debido a una reacción de combustión y es comúnmente aplicado en el estudio de combustibles. La comida es similar a combustibles hidrocarburo y carbohidrato y cuando se oxida su contenido calórico es similar (sin valorarlo de la misma forma que un hidrocarburo). En termodinámica química el término utilizado para la energía potencial química es potencial químico y para la transformación química una ecuación sumamente utilizada es la ecuación Gibbs-Duhem.
Reacciones químicas
En muchos casos de interés en la termodinámica química existen grados de libertad internos y procesos como reacciones químicas y transiciones de fase, las cuales siempre generan entropía a menos que se encuentren en equilibrio o mantenidas en un "equilibrio constante" a través de cambios "cuasi-estáticos" al ser sumados a dispositivos limitantes como pistones o electrodos, con el fin de entregar y recibir trabajo externo. Incluso para materiales "bulto" homogéneos las funciones de energía libre dependen de la composición, así como potenciales termodinámicos extensivos, incluyendo la energía interna. Si las cantidades { Ni }, el número de especies químicas son omitidos de la fórmula, es imposible describir cambios en la composición.
Función Gibbs
Para un sistema "bulto" (no estructurado) hay variables extensivas. Para un sistema "bulto" homogéneo no estructurado, aún hay varias variables composicionales "extensivas" { Ni } que G depende de, el cual especifica la composición, la cantidad de cada sustancia química, expresada como el número de moléculas presentes o (divididas por el número de Avogadro), el número de moles.
Para el caso en donde únicamente PV realizan trabajo es posible
en donde μi es el potencial químico para el i-ésimo componente en el sistema
La expresión para dG es muy útil a T y P constantes, condiciones que son fáciles de alcanzar de manera experimental y que aproximan la condición en criaturasvivientes
Afinidad química
Mientras esta formulación es matemáticamente justificable, no es particularmente clara desde que no se puede de manera simple remover o añadir moléculas de un sistema. Siempre hay un proceso involucrado en cambiar la composición; por ejemplo, una (o varias) reacciones químicas o movimiento de moléculas de una fase (líquida) a otra (gas o sólida). Debemos encontrar la notación que no parezca insinuar que la cantidad de componentes ( Ni } puede ser cambiado de manera independiente. Todos los procesos reales obedecen a la conservación de masa y además, la conservación del número de átomos de cada clase. Sin importar las moléculas transferidas hacia o desde, deben considerarse parte del "sistema".
Consecuentemente se introduce una variable explícita para representar el grado de avance de un proceso, una variable de progreso, ξ para el alcance de la reacción(Prigogine & Defay, p. 18; Prigogine, pp. 4–7; Guggenheim, p. 37.62), y para el uso de la derivada parcial ∂G/∂ξ (en lugar del muy utilizado "ΔG", desde que la cantidad en cuestión no es una carga finita). El resultado es una clara expresión para la dependencia de dG en reacciones químicas (u otros procesos). Si hay sólo una reacción
Si introducimos el coeficiente estequiométrico para el i-ésimo componente en la reacción
que dice cuántas moléculas de i son producidas o consumidas, obtenemos una expresión algebraica para la derivada parcial
donde, (De Donder; Progoine & Defay, p. 69; Guggenheim, pp. 37,240), se introduce un histórico y conciso nombre para esta cantidad, la "afinidad", simbolizada con una A, introducida por Théophile de Donder en 1923. El signo menos viene de la aseveración de que la afinidad fue definida para representar la regla acerca de que los cambios espontáneos siempre ocurren cuando el cambio en la energía libre de Gibbs del proceso es negativo, significando que las especies químicas tienen una afinidad positiva entre ellas. El diferencial para G toma una forma simple que muestra su dependencia en el cambio composicional
Si hay un número de reacciones químicas llevándose a cabo de manera simultánea, como es el caso de
una serie de reacciones coordinan { ξj }, evadiendo la idea que de la cantidad de componentes ( Ni } puede ser cambiado de manera independiente. Las expresiones mostradas anteriormente son iguales a cero en el equilibrio termodinámico, mientras que en el caso general para sistemas reales son negativos, ya que todas las reacciones químicas generadas en un rango finito produce entropía. Esto se puede hacer aún más explícito al introducir los rangos de la reacción dξj/dt. Para cada y todo proceso físicamente independiente (Prigogine & Defay, p. 38; Prigogine, p. 24)
Este es un resultado significativo desde que los potenciales químicos son variables intensivas de un sistema, dependiendo sólo del entorno local molecular. No pueden "saber" si la temperatura y presión (u otras variables de sistema) van a ser constantes a lo largo del tiempo. Es un criterio puramente local y debe permanecer a pesar de cualquier otra constante. Por supuesto pudo ser obtenido al tomar derivadas parciales de cualquier otra de las funciones fundamentales de estado, pero no obstante es un criterio general para (−T veces) la producción de entropía de un proceso espontáneo o al menos cualquier parte de la misma que no es tomada como trabajo externo. (Ver Restricciones abajo).
Ahora dejamos descansar el requerimiento de un sistema “bulto” homogéneo al permitir que los potenciales químicos y la afinidad aplicada a cada localidad en que una reacción química (o cualquier otro proceso) está llevándose a cabo. Tomando en cuenta la producción de entropía debido a procesos irreversibles, la desigualdad para dG es ahora reemplazada por una igualdad
o
Cualquier disminución en la función Gibbs de un sistema es el límite superior para cualquier trabajo isotérmico, isobárico que pueda ser capturado en los alrededores, o podría ser simplemente disipado, mostrándose como T veces un incremento correspondiente en la entropía del sistema y/o su entorno. O podría en parte ir hacia un trabajo externo y parte hacia crear entropía. El punto importante es que el alcance de reacción para una reacción química debe ser emparejado con el desplazamiento de una cantidad mecánica o eléctrica externa de una manera en que una pueda avanzar únicamente si la otra lo hace. El emparejamiento puede ser ocasionalmente rígido, pero es a menudo flexible y variable.
Soluciones
En solución química y bioquímica, la energía libre de Gibbs decrece (∂G/∂ξ, en unidades molares, denotada de forma críptica por ΔG) es comúnmente utilizada como un sustituto para (−T veces) la entropía producida por reacciones químicas espontáneas en situaciones donde no se ha realizado trabajo, o al menos no trabajo "útil"; por ejemplo, aparte de, quizás alguna ± PdV. La afirmación de que toda toda reacción espontánea tiene una ΔG negativa es simplemente una reafirmación de la relación termodinámica fundamental, otorgándole las dimensiones físicas de energía y en cierto modo oscureciendo su significado en términos de entropía. Cuando no hay un trabajo útil que se realice, será menos engañoso utilizar las transformaciones Legendre de la entropía apropiadas para la constante T o para la constante T y P, las funciones Massieu −F/T y −G/T respectivamente.
No equilibrio
Generalmente los sistemas tratados con la termodinámica química convencional están en equilibrio o cerca de éste. Ilya Prigogine desarrolló el tratamiento termodinámico de sistemas abiertos que están lejos del equilibrio. Realizando este trabajo descubrió fenómenos y estructuras de tipos completamente nuevos e inesperados. Su termodinámica generalizada, no linear e irreversible encontró sorprendentes aplicaciones en una gran variedad de campos.
La termodinámica del no equilibrio ha sido aplicada para explicar cómo estructuras ordenadas, por ejemplo sistemas biológicos, pueden desarrollarse a partir del desorden. Aún si las relaciones Onsager son utilizadas, los principios clásicos del equilibrio en termodinámica todavía muestran que los sistemas lineales cercanos al equilibrio siempre desarrollan estados de desorden que son estables ante perturbaciones y no pueden explicar la existencia de estructuras ordenadas.
Prigogine llamó a estos sistemas sistemas disipativos porque están formados y sostenidos por procesos disipativos que se llevan a cabo debido al intercambio de energía entre el sistema y su ambiente y porque desaparecen si ese intercambio se interrumpe. Comúnmente se dice que viven en simbiosis con su ambiente.
El método que Prigogine utilizó para estudiar la estabilidad de las estructuras disipativas frente a perturbaciones es de gran interés general. Hace posible el estudio de problemas variados como problemas de tránsito en la ciudad, la estabilidad de comunidades de insectos, el desarrollo de estructuras biológicas ordenadas y el crecimiento de las células cancerosas por mencionar algunos ejemplos.
Restricciones del sistema
En esta consideración, es esencial entender el rol de las paredes y otras restricciones y la distinción entre procesos independientes y acoplamiento. Contrario a las claras implicaciones de varias fuentes de referencia, el análisis previo no está restringido a sistemas bulto homogéneos e isotrópicos que pueden entregar únicamente trabajoPdV al mundo exterior, pero aplica a los sistemas más estructurados. Existen sistemas complejos con muchas "reacciones" químicas ocurriendo al mismo tiempo, algunas de las cuales son sólo partes del proceso general. Un proceso "independiente" es el que "puede" llevarse a cabo incluso si otros son inexplicablemente detenidos en su camino. Entendiendo esto probablemente como un “experimento de ideas” en cinética química, pero ejemplos actuales existen.
Una reacción de gas que resulta en un incremento en el número de moléculas conducirá a un incremento en el volumen a una presión externa constante. Si ocurre dentro de un cilindro cerrado con un pistón, la reacción equilibrada puede proceder sólo realizando trabajo en contra de una fuerza externa en el pistón. La variable extensiva para la reacción puede incrementar sólo si el pistón se mueve y a la inversa, si el pistón es presionado hacia dentro entonces la reacción se lleva a cabo al revés.
De manera similar, una reacción redox puede ocurrir en una celda electroquímica con el paso de corriente en los cables que conectan los electrodos. Las medias reacciones en la celda y electrodos están restringidas si no existe corriente que fluya en la celda. La corriente puede ser disipada como calor en joules o puede utilizarse como un dispositivo eléctrico, por ejemplo motor realizando trabajo mecánico. Una batería de automóvil plomo-ácido se puede recargar, conduciendo la reacción química de manera inversa. En este caso la reacción no es un proceso independiente. Algunas, posiblemente la mayoría, de las reacciones con energía libre de Gibbs pueden distribuirse como trabajo externo.
La hidrólisis del ATP a ADP y fosfato puede conducir el trabajo fuerza distancia entregado por músculos vivos y la síntesis del ATP es conducida por una cadena redox en la mitocondria y cloroplastos, que involucran el transporte de iones cruzando las membranas de éstos organelos celulares. El emparejamiento de los procesos aquí y en los ejemplos siguientes es a menudo incompleto. El gas puede fugarse lentamente de un pistón, justo como si pudiera fugarse lentamente de un globo de caucho. Algunas reacciones pueden ocurrir en la batería aún si no fluye corriente externa. Usualmente hay un coeficiente de emparejamiento, el cual depende de índices relativos y que determina el porcentaje de la energía libre manejada convertida en trabajo externo o capturada como "trabajo químico"; un nombre poco apropiado para la energía libre de otro proceso químico.
Tipos de sistemas termodinámicos
Los sistemas termodinámicos se clasifican en sistemas abiertos, cerrados o aislados según su capacidad para intercambiar materia y energía con el entorno. Así:
- Sistema abierto: puede intercambiar con el entorno tanto materia como energía
, generalmente en forma de calor. Por ejemplo, la combustión de madera al aire libre, o una reacción química en un vaso de laboratorio abierto, que permite tanto el paso de calor a través de las paredes del recipiente (se dice que el recipiente tiene paredes diatérmicas) como desprendimiento de gases. - Sistema cerrado: puede intercambiar energía con el entorno, pero no materia. Por ejemplo, un recipiente cerrado de vidrio en el que se lleva a cabo una reacción química que desprende calor. Los gases formados no pueden abandonar dicho recipiente porque está cerrado con un tapón, pero el calor sí que puede desprenderse porque las paredes de vidrio son diatérmicas. Si tocamos el recipiente con las manos, lo notaremos caliente.
- Sistema asilado: no es posible el intercambio ni de materia ni de energía. Por ejemplo, lo que se conoce coloquialmente como un termo, que técnicamente es un vaso Dewar y que se usa para llevar infusiones o café y que se mantengan calientes más tiempo, es en teoría un sistema aislado, que no permite ni el paso de materia ni de energía. No obstante, los sistemas aislados son teóricos, en la práctica siempre hay cierto intercambio leve de energía y al final, el café se acaba enfriando (¡mala suerte!).
Calorímetro de laboratorio: ejemplo de sistema aislado
Asimismo, los sistemas reaccionantes también se pueden clasificar en función del estado de agregación de reactivos y productos. Si todos los componentes se halla en el mismo estado de agregación (sólido, líquido o gas), es decir, tenemos una sola fase, tendremos lo que se denomina un sistema homogéneo. Por ejemplo, la combustión del metano es un sistema homogéneo, ya que todos los componentes son gases:
Si tenemos componentes con distintos estados de agregación, es decir, tenemos varias fases, entonces se trata de un sistema heterogéneo. Por ejemplo, la descomposición de carbonato de magnesio sólido por calcinación con desprendimiento de dióxido de carbono:
Especificados ya los tipos de sistemas termodinámicos que existen, en el Apartado 2 de teoría de Termoquímica nos centraremos en el estudio de las llamadas variables termodinámicas.
Tipos de Variables termodinámicas: extensivas e intensivas
Las variables termodinámicas se clasifican en dos tipos, atendiendo a su dependencia o independencia con la cantidad total de materia presente en el sistema. Así, tenemos:
- Variables extensivas: si su valor depende de la cantidad o porción de sistema que se considera, por ejemplo: masa, volumen, número de moles…
- Variables intensivas: si su valor no depende de la cantidad de sistema considerado, por ejemplo: temperatura, densidad, presión, concentración…
P·V = n·R·T
Donde:
P = presión (atm o pascales, Pa)
V = volumen (litros o m3)
n = número de moles
R = constante de los gases ideales, 0,082 atm·l/K·mol o 8,31 J/K·mol
T = temperatura en grados kelvin (K)
Dada esta ecuación para los gases ideales, bastará conocer la presión, el volumen y la temperatura para definir el estado del sistema, y el número de moles, o la densidad, o la masa, se podrían calcular conociendo dichos valores de P, V y T. Por tanto, con estas variables el sistema quedaría totalmente descrito.
Procesos isotermos, isobáricos, isocoros y adiabáticos
- A los procesos que se llevan a cabo a temperatura constante, se los denomina isotermos o isotérmicos (T = cte)
- A los procesos que se llevan a cabo a presión constante, se los denomina isobáricos (P = cte)
- A los procesos que se llevan a cabo a volumen constante, se los denomina isocoros (V = cte)
- A los procesos que se llevan a cabo sin transferencia de calor entre el sistema y el entorno, se los llama adiabáticos (Q = 0)
Definición de función de estado
Por último, aunque no por ello menos importante, debemos saber que algunas variables termodinámicas son, además, lo que se conoce como funciones de estado. ¿Qué significa esto? Significa que si el sistema sufre una modificación y pasa de un estado A a un estado B, el valor de estas variables termodinámicas que son funciones de estado no depende de cómo se ha efectuado la transformación, sólo del estado del sistema.
Veremos esto con un ejemplo concreto para que sea más sencillo, tomando como variable la temperatura. Consideremos un sistema que está en un estado A en el cual la temperatura es de 20ºC. Este sistema sufre una transformación y pasa a estar en un estado B en el cual la temperatura es de 60ºC. El sistema en le estado B seguirá estando a 60ºC independientemente delcamino que haya seguido la transformación. No depende del camino que ha seguido dicha transformación, no importa si se ha calentado y luego enfriado, o si se ha calentado progresivamente… La temperatura en el estado B seguirá siendo de 60ºC, sin importar cómo se ha llegado a ello. Por esto, la temperatura es una función de estado, sólo depende del estado del sistema en el momento en que lo consideremos.
Otra forma de decir esto es que las variaciones que experimentan las funciones de estado sólo dependen del estado inicial y final del sistema. En nuestro caso la variación de temperatura es de 40ºC (60 – 20).
Otras variables termodinámicas que son función de estado son el volumen, la presión, y otros nuevos conceptos en los que vamos a profundizar a lo largo del tema como la energía interna, la entalpía, la entropía y la energía libre de Gibbs.
¿Qué es el trabajo de compresión o expansión de un gas?
W = -Fext·Δx
Y la fuerza es presión·superficie: Fext = P·S
W = -P·S·Δx
Mientras que la superficie por la variación de x que sufre el émbolo es la variación de volumen que experimenta el recipiente:
S·Δx = ΔV
De modo que finalmente el trabajo de expansión es:
Criterio de signos en el trabajo de compresión y expansión de un gas
Si aumenta el volumen, es el gas, es decir, el sistema, el que realiza un trabajo mecánico. Según el criterio de signo que adoptaremos, que es el establecido por la IUPAC, este trabajo realizado por el sistema se considera de signo negativo, es decir, W < 0.
Si disminuye el volumen, es el entorno el que ejerce un trabajo sobre el sistema, en cuyo caso, según el criterio de signos establecido por la IUPAC, consideraremos que le trabajo es positivo, W > 0.
NOTA: Es posible que en algunos textos se halle un criterio de signos distinto a este para el trabajo, considerándose que W = +P·ΔV y que por tanto W > 0 para el trabajo realizado por el sistema y W < 0 para le trabajo realizado sobre el sistema. Esto es habitual en tratados de física y de ingenierías, aunque para química lo más habitual es considerar el criterio de signos expuesto aquí, que es el establecido por la IUPAC.
Ejemplo numérico simple de cálculo del trabajo de expansión de un gas
Un gas se expande de un volumen inicial de 4 litros a un volumen de 9 litros, contra una presión externa constante de 2 atmósferas. Calcular el trabajo realizado por el sistema.
en el primer apartado introductorio sobre termoquímica los procesos químicos y físicos de las sustancias llevan asociados cambios o variaciones de energía, y la forma de energía más habitual de dichas variaciones es como calor o energía calorífica. El intercambio de calor entre un sistema y su entorno se produce como consecuencia de una diferencia de temperatura, por ejemplo:
Siempre se produce un flujo de calor desde el elemento de mayor temperatura al de menor temperatura. En concreto, la transferencia de calor, Q, que experimenta un sistema formado por una sustancia pura depende de:
- La variación de temperatura que experimenta, ΔT
- La masa de la sustancia, m
La naturaleza de la sustancia. De dicha naturaleza dependen dos parámetros que vamos a definir a continuación, la capacidad calorífica específica y la capacidad calorífica molar.
Capacidad calorífica específica o calor específico de una sustancia
La capacidad calorífica, c, o calor específico, es la energía calorífica necesaria para aumentar 1ºC o 1K (si hablamos de incrementos es lo mismo) la temperatura de 1kg de masa de una sustancia a una presión de 1013 hPa, En el SI se expresa en J/kg·K y es una propiedad característica de las sustancias.
Esto significa que para que un kg de agua aumente 1ºC su temperatura a presión normal, se han de suministrar 4180 J de energía calorífica.
En general, conociendo la masa de sustancia, m, la variación de temperatura que experimenta, ΔT, y su capacidad calorífica específica se puede calcular la energía calorífica intercambiada o transferencia de calor, Q, según la fórmula:
Q=m·c·ΔT
Donde:
m = masa de la sustancia
c = capacidad calorífica específica (J/K·kg)
ΔT = Tf – Ti (temperatura final menos temperatura inicial del sistema)
Por ejemplo, para calentar una barra de 6kg de aluminio de 25ºC a 40ºC, sabiendo que la C del aluminio es de 895 J/kg·K
Q = m·c·ΔT = 6 kg · 895 (J/K·kg) · (40-25) = 80550 J
Capacidad calorífica molar de una sustancia
La Capacidad calorífica molar, Cm, es la energía calorífica necesaria para aumentar 1K o 1ºC la temperatura de un mol de cualquier sustancia. En este caso, la transferencia de calor será:
Q= n·ΔT·Cm
Donde:
n = número de moles
Cm = capacidad calorífica molar
ΔT = Tf – Ti (temperatura final menos temperatura inicial del sistema)
primer apartado introductorio sobre termoquímica, que toda reacción química obedece a dos leyes fundamentales, la Ley de conservación de la masa y la Ley de conservación de la energía. Es esta segunda, la Ley de Conservación de la Energía, la que constituye o surge del Primer Principio de la Termodinámica o Primera Ley de la Termodinámica. Este Primer Principio establece, por tanto, que la energía siempre se conserva, de modo que si en un sistema capaz de intercambiar energía, la energía disminuye, necesariamente aparecerá una cantidad de energía equivalente en el entorno, ya que la energía no se crea ni se destruye, sólo se transforma.
Matemáticamente, el Primer Principio de la Termodinámica determina cómo afectan los intercambios de calor, Q, y trabajo, W, a la energía global de un sistema. Es por este motivo que la transferencia de energía en forma de calor y la transferencia de energía en forma de trabajo las hemos tratado en dos apartados previos de teoría.
Así, la ecuación matemática del Primer Principio es:
Siendo, según el criterio de signos establecido por la IUPAC, y explicado en el apartado 3, positivo el calor y el trabajo que entra o se realiza sobre el sistema, y negativo el calor que sale del sistema o el trabajo realizado por el mismo.
U es una función de estado que introducimos por primera vez en este tema y que recibe el nombre de energía interna del sistema. Así, se puede enunciar la Primera Ley de la Termodinámicacomo:
Pero… ¿qué es la energía interna de un sistema? Es la energía asociada a la estructura interna del sistema, es decir, la suma de todas las energías contenidas en el mismo, como la energía cinética de sus partículas individuales (núcleos, átomos, moléculas… que pueden vibrar, rotar o incluso efectuar movimientos de traslación, como los gases) y la energía potencial de éstas, esencialmente energía potencial eléctrica debida a atracciones núcleo-electrón, repulsiones núcleo-núcleo y repulsiones electrón-electrón.
El valor absoluto de la energía interna de un sistema, U, se desconoce por su gran complejidad, pero sí que podemos medir o determinar su variación, ΔU, cuando pasa de un estado inicial a un estado final, ya que, como hemos dicho, la energía interna es una función de estado y sólo depende de dichos estados inicial y final:
En cuanto a la aplicación del Primer Principio de la Termodinámica a las reacciones químicas, que es lo que nos interesa en este caso, la variación de energía interna representa la diferencia de energía entre los productos y los reactivos, siendo Q y W la transferencia de calor como calor y como trabajo que acompañan a dicha reacción química.
A continuación, en los dos siguientes apartados, vamos a estudiar para una reacción la transferencia de calor a volumen constante y la transferencia de calor a presión constante.
Existen algunas reacciones química que transcurren a volumen constante, es decir, sin variación apreciable en el volumen total del sistema. Son ejemplos de ello las reacciones que se dan entre sólidos y líquidos sin desprendimiento de gases, ya que en estos la variación es muy pequeña y se puede despreciar, o también las que se llevan a cabo en un recipiente cerrado, como un termo o un calorímetro, aunque intervengan gases. Son ejemplos de esto la comida cocinada en la olla a presión, la esterilización del material de laboratorio en un autoclave o la fermentación del vino en un recipiente cerrado para convertirse en cava.
y que hemos deducido en el tercer apartado
De modo que:
Como el proceso es a volumen constante, éste será el calor transmitido a volumen constante lo cual se indica añadiendo v subíndice.
Termodinámica a las reacciones que transcurren a volumen constante, en cuyo caso la transferencia de calor recibe el nombre de Qv, y a las reacciones que transcurren a presión constante, que da lugar a QP. Asimismo, hemos deducido que:
ΔU = QV y ΔH = QP
A partir de esto podemos deducir la relación entre la variación de entalpía y la variación de energía interna.
Relación entre QP y QV para sólidos y líquidos
QP = QV, o también, ΔH = ΔU
Relación entre QP y QV para gases
En cambio, si en las reacciones intervienen especies gaseosas, que haya o no variación de volumen dependerá de la variación del número de moles de especies gaseosas enre reactivos y productos:
PV = nRT
PΔV = ΔnRT
PΔV = ΔnRT
Utilizamos la ecuación ya conocida QP = ΔU + PΔV y sustituiremos PΔV por ΔnRT y obtenedremos:
Sólo si Δn = 0, entonces QP = QV, sino QP ≠ QV
Para calcular Δn en una reacción vamos a ver un ejemplo concreto, consideremos la reacción de combustión del metano:
La variación del número de moles corresponde a la suma de los coeficientes estequiométricos de los productos menos la suma de los coeficientes estequiométricos de los reactivos, es decir:



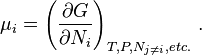




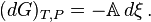




No hay comentarios:
Publicar un comentario