Algoritmos de búsqueda de raíces
método de Broyden es un método cuasinewtoniano para la solución numérica de ecuaciones no lineales con más de una variable. Fue descrito originalmente por C. G. Broyden en 1965.1
Para hallar la solución de la ecuación  , el método de Newton emplea el jacobiano
, el método de Newton emplea el jacobiano  en cada iteración. Sin embargo, computar ese jacobiano es una operación difícil y costosa. La idea que subyace en el método de Broyden consiste en computar el jacobiano entero solamente en la primera iteración, y llevar a cabo una actualización de rango 1 en las demás iteraciones.
en cada iteración. Sin embargo, computar ese jacobiano es una operación difícil y costosa. La idea que subyace en el método de Broyden consiste en computar el jacobiano entero solamente en la primera iteración, y llevar a cabo una actualización de rango 1 en las demás iteraciones.
 , el método de Newton emplea el jacobiano
, el método de Newton emplea el jacobiano  en cada iteración. Sin embargo, computar ese jacobiano es una operación difícil y costosa. La idea que subyace en el método de Broyden consiste en computar el jacobiano entero solamente en la primera iteración, y llevar a cabo una actualización de rango 1 en las demás iteraciones.
en cada iteración. Sin embargo, computar ese jacobiano es una operación difícil y costosa. La idea que subyace en el método de Broyden consiste en computar el jacobiano entero solamente en la primera iteración, y llevar a cabo una actualización de rango 1 en las demás iteraciones.
En 1979, Gay demostró que, cuando se aplica el método de Broyden a un sistema lineal, se requieren 2n pasos.
Descripción del método
El método de Broyden considera el método de la secante y establece una generalización de él para el espacio multidimensional.
y procede según el método de Newton:
Broyden establece una generalización de esa fórmula para un sistema de ecuaciones mediante una sustitución de la derivada  por el jacobiano
por el jacobiano  . Éste se determina por medio de la ecuación de la secante (la aproximación de diferencia finita):
. Éste se determina por medio de la ecuación de la secante (la aproximación de diferencia finita):
 por el jacobiano
por el jacobiano  . Éste se determina por medio de la ecuación de la secante (la aproximación de diferencia finita):
. Éste se determina por medio de la ecuación de la secante (la aproximación de diferencia finita):
Sin embargo, esta ecuación está infradeterminada por más de una dimensión.
Broyden sugiere un procedimiento que consta de los siguientes 3 pasos:
1) Emplear la aproximación del jacobiano 

2) Tomar la solución de la ecuación de la secante que suponga la modificación mínima de  (entendiendo por mínima que se dé una minimización de la norma de Frobenius
(entendiendo por mínima que se dé una minimización de la norma de Frobenius  )
)
 (entendiendo por mínima que se dé una minimización de la norma de Frobenius
(entendiendo por mínima que se dé una minimización de la norma de Frobenius  )
)
3) Continuar según el método de Newton:
En esa última fórmula,
y
son vectores columna de k elementos en un sistema de k dimensiones.
Así:
Broyden sugiere también emplear la fórmula de Sherman-Morrison para actualizar directamente el inverso del jacobiano:
Éste último se conoce como el « buen método de Broyden».
Se puede obtener a partir de él una técnica similar empleando una modificación ligeramente distinta de  que minimiza en su lugar
que minimiza en su lugar 
 que minimiza en su lugar
que minimiza en su lugar 
Tal sería el llamado « mal método de Broyden»:
Pero, en cuanto a lo de « mal método», véase "A faster Broyden method" ("Un método de Broyden más rápido").3
Se han sugerido muchos otros procedimientos cuasinewtonianos en el campo de la optimización, en el que se busca un máximo o un mínimo hallando la raíz de la primera derivada, o el gradiente si se trata de un espacio multidimensional. Se califica al jacobiano del gradiente de «hessiano», y es simétrico, lo que añaderestricciones a la hora de llevar a cabo su actualización.
Método de Broyden
f(xk)-f(xk-1)=A(xk-xk-1)
Por el contrario en el caso no lineal la igualdad anterior no se cumple aunque se puede lograr, eligiendo adecuadamente A, que
f(xk)-f(xk-1)≈Ak(xk-xk-1)
en si no el método no se ve muy complicado de lo expuesto hasta ahora, pero considerando los calculo que se realizan por cada iteración se ve la debilidad del método, para calcular el jacobiano asociado a un sistema de n ecuaciones no lineales requiere determinar y evaluar n derivadas parciales. Cuando no es práctico efectuar la evaluación exacta, podemos usar la aproximacion de diferencia finita a las derivadas parciales
∂fj(xi)/ ∂xk ≈ (fj(xi+ekh)-fj(xi))/h
Sin embargo está aproximación requiere efectuar, al menos, n2 evaluciones de funciones escalares para aproximar la matriz jacobiana y no disminuye la cantidad de cálculos, casi siempre es necesario O(n3) para resolver el sistema. Por lo tanto, el total de cálculos que se requiere para una sola iteración del método es almenos n2+n evaluaciones de funciones escalares(n2 para evaluar la matriz jacobiana y n para evaluar f), junto con O(n3) operaciones aritmeticas para resolver el sistema lineal. Asi la cantidad de cálculos aumenta conforme aumenta la cantidad de ecuaciones del sistema en el caso del método de Newton pero con el método de Broyden tiene una convergencia superlineal.
Generalizando para mas dimensiones la aproximación por la derivada de imagen 1 obtenemos
Jk(xk-xk-1) ≈ f(xk)-f(xk-1)
entonces según el método de newton las iteraciones seran segun
xk = xk-1 + Jk-1[ f(xk) ]
y para cada iteración usamos la siguiente formula propuesta por broyden para hallar el jacobiano J
Jk = Jk-1 + [ (∇yk-Jk-1∇sk) / ||∇sk||2 ] ∇skT
donde
∇y = f(xk)-f(xk-1) ∇sk = xk-xk-1
método de Bairstow es un algoritmo eficiente de búsqueda de las raíces de un polinomio real de grado arbitrario. Es un método iterativo, basado en el método de Müller y de Newton Raphson. Dado un polinonio
 se encuentran dos factores, un polinomio cuadrático se encuentran dos factores, un polinomio cuadrático
El procedimiento general para el método de Bairstow es el siguiente. Dado:
La principal diferencia de este método, respecto a otros, es que permite calcular todas las raíces de un polinomio (reales e imaginarias).
Para calcular la división de polinomios, hacemos uso de la división sintética. Así dado:
Al dividir entre
 , se tiene como resultado el siguiente polinomio: , se tiene como resultado el siguiente polinomio:
con un residuo
 , el residuo será cero solo si , el residuo será cero solo si  lo son. lo son.
Los términos b, se calculan utilizando división sintética, la cual puede resolverse utilizando la siguiente relación de recurrencia:
Una manera de determinar los valores de r y s que hacen cero el residuo es utilizar el método de Newton-Raphson. Para ello necesitamos una aproximación lineal de
 respecto a r y s la cual calculamos utilizando la serie de Taylor respecto a r y s la cual calculamos utilizando la serie de Taylor
donde los valores de r y s están dados y se calculan los incrementos dr y ds que hacen a
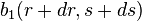 y y  igual a cero. El sistema de ecuaciones que se tiene que resolver es: igual a cero. El sistema de ecuaciones que se tiene que resolver es:
Bairtow muestra que las derivadas parciales pueden obtener haciendo un procedimiento similar a la división sintética, así:
donde:
El algoritmo de Bairstow tiene orden de convergencia cuadrático como el método de Newton, excepto en el caso de que el polinomio tenga factores cuadráticos de multiplicidad superior a 1, pudiendo ser el orden de convergencia menor. Metodo de Bairstow. Raices de Polinomios .- ......................................:http://www.academia.edu/3524281/Metodo_de_Bairstow._Raices_de_Polinomios |
 por la
por la 
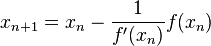



![\displaystyle x_n=(x_1[n],...,x_k[n])](https://upload.wikimedia.org/math/b/9/c/b9c074d35605a109d98ff9b71f991ab1.png)
![\displaystyle F_n(x)=(f_1(x_1[n],...,x_k[n]),...,f_k(x_1[n],...,x_k[n])](https://upload.wikimedia.org/math/3/1/a/31a4e10ea4f791f3aaf410bcb6e4ed35.png)
![\Delta x_n=\begin{bmatrix}
x_1[n]-x_1[n-1]\\
...\\
x_k[n]-x_k[n-1]
\end{bmatrix}
\quad \text{y} \quad
\Delta F_n=\begin{bmatrix}
f_1(x_1[n],...,x_k[n])-f_1(x_1[n-1],...,x_k[n-1])\\
...\\
f_k(x_1[n],...,x_k[n])-f_k(x_1[n-1],...,x_k[n-1])
\end{bmatrix}.](https://upload.wikimedia.org/math/8/5/1/85184037710a1a9f96676c014ea7eefa.png)




 y
y 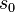
 sea igual a cero.
sea igual a cero. , utilizando la formula general.
, utilizando la formula general.







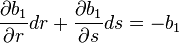






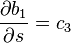
No hay comentarios:
Publicar un comentario