viernes, 30 de octubre de 2015

Algoritmos

Algoritmos de búsqueda de raíces

algoritmo de búsqueda de raíces es un método numérico o algorítmico para encontrar las soluciones aproximadas de una ecuación dada por la expresión f(x) = 0 para una función matemática f dada. A la solución x de la ecuación se le llama raíz o cero de la función.
Igualmente, resolver la ecuación f(x) = g(x) es análogo a resolver la ecuación f − g = 0, es decir, encontrar las raíces de la función f - g.
Este artículo trata sobre cómo encontrar raíces reales ó complejas, aproximadas por números de punto flotante.
Los métodos numéricos de resolución de ecuaciones no lineales suelen ser métodos iterativos que producen una sucesión de valores aproximados de la solución, que se espera, que converja a la raíz de la ecuación. Estos métodos van calculando las sucesivas aproximaciones sobre la base de los anteriores, a partir de una o varias aproximaciones iniciales.
El comportamiento de los algoritmos de búsqueda de raíces se estudia en análisis numérico. Funcionan mejor cuando se toman en cuenta las características de la función. Para saber que método debemos aplicar, hay que tener en cuenta la capacidad de separar raíces cercanas, confiabilidad en el alcance de soluciones evitando errores numéricos graves y orden de convergencia.
Los siguientes métodos son para calcular las raíces reales de una ecuación dada por f(x) = 0 donde se exige al menos que la función fsea una función continua para garantizar la existencia de solución. La mayoría de métodos se obtienen de interpolar la función, generalmente mediante un polinomio de primer grado (interpolación lineal) y después aproximar la solución mediante alguna de las raíces del polinomio.
El algoritmo más simple de búsqueda de raíces es el método de bisección. Requiere un intervalo inicial que contenga alguna raíz de la ecuación (de forma que la función tome en los extremos del mismo valores de distinto signo; véase el teorema de Bolzano). Dicho intervalo inicial se va dividiendo sucesivamente por la mitad (se bisecta) tomándose el intervalo que contiene a la raíz. A pesar de ser un método que siempre converge a una solución, converge muy lentamente.
El método de Newton asume que la función f sea continuamente derivable y que se conoce la derivada de la función. Este método puede no converger si se comienza con un valor muy alejado de la raíz. Sin embargo, si converge, lo hace mucho más rápido que el método de bisección (usualmente, de manera cuadrática), por eso el número de dígitos correctos se duplica en cada iteración. El método de Newton también es útil porque se generaliza para problemas de dimensiones más altas.
Reemplazando la derivada del método de Newton por un cociente incremental, obtenemos el método de la secante. Este método no requiere el cálculo (ni la existencia) de la derivada, pero el precio que se debe pagar es un orden de convergencia más bajo (aproximadamente 1.6).
El método de la regla falsa (o regula falsi) es un método que combina lo mejor del método de bisección y del método de la secante. El método corta el intervalo en dos partes como en el método de bisección, pero a diferencia de éste, lo corta por el valor obtenido aplicando el método de la secante a los extremos del intervalo, no siendo generalmente las partes iguales. El método converge siempre a una raíz de la ecuación, generalmente de forma más rápida que el método de bisección pero más lenta que el método de la secante.
Finalmente, hay una familia de métodos conocidos como métodos de punto fijo. Estos métodos se basan en obtener a partir de la ecuación f(x) = 0 una ecuación equivalente de la forma g(x) = x cuya solución se convierta en un punto fijo de g e iterando a partir de un valor inicial hasta que se alcance.

métodos de resolución numéricos de ecuaciones no lineales .- .............................................::http://ocw.upm.es/matematica-aplicada/programacion-y-metodos-numericos/contenidos/TEMA_8/Apuntes/EcsNoLin.pdf













método de bisección es un algoritmo de búsqueda de raíces que trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que tiene la raíz.

Introducción

Este es uno de los métodos más sencillos y de fácil intuición para resolver ecuaciones en una variable, también conocido como Método de Intervalo Medio.1 Se basa en el teorema del valor intermedio (TVI), el cual establece que toda función continua f en un intervalo cerrado [a,b] toma todos los valores que se hallan entre f(a) y f(b). Esto es que todo valor entref(a) y f(b) es la imagen de al menos un valor en el intervalo [a,b]. En caso de que f(a) y f(b) tengan signos opuestos, el valor cero sería un valor intermedio entre f(j) y f(e), por lo que con certeza existe un p en [a,b] que cumple f(p)=0. De esta forma, se asegura la existencia de al menos una solución de la ecuación f(a)=0.
El método consiste en lo siguiente:
  • Debe existir seguridad sobre la continuidad de la función f(x) en el intervalo [a,b]
  • A continuación se verifica que \scriptstyle f(a)\cdot f(b) <0
  • Se calcula el punto medio m del intervalo [a,b] y se evalúa f(m) si ese valor es igual a cero, ya hemos encontrado la raíz buscada
  • En caso de que no lo sea, verificamos si f(m) tiene signo opuesto con f(a) o con f(b)
  • Se redefine el intervalo [a, b] como [a, m] ó [m, b] según se haya determinado en cuál de estos intervalos ocurre un cambio de signo
  • Con este nuevo intervalo se continúa sucesivamente encerrando la solución en un intervalo cada vez más pequeño, hasta alcanzar la precisión deseada
En la siguiente figura se ilustra el procedimiento descrito.
El método de bisección es menos eficiente que el método de Newton, pero es mucho más seguro para garantizar la convergencia. Si f es una función continua en el intervalo [a, b] y f(a)f(b) < 0, entonces este método converge a la raíz de f. De hecho, una cota del error absoluto es:
\frac{\left|b-a\right|}{2^n}
en la n-ésima iteración. La bisección converge linealmente, por lo cual es un poco lento. Sin embargo, se garantiza la convergencia si f(a) y f(b) tienen distinto signo.
Si existieran más de una raíz en el intervalo entonces el método sigue siendo convergente pero no resulta tan fácil caracterizar hacia qué raíz converge el método.

Algoritmo

Para aplicar el método consideremos tres sucesiones a_n \le p_n \le b_n\, definidas por las siguientes relaciones:
p_n = \frac{a_n+b_n}{2}, \quad a_{n+1} = \begin{cases} a_n & \mbox{si } f(a_n)\cdot f(p_n) <0 \\ p_n & \mbox{si } f(a_n)\cdot f(p_n) > 0\end{cases}, \quad b_{n+1} = \begin{cases} b_n & \mbox{si } f(b_n)\cdot f(p_n) < 0 \\ p_n & \mbox{si } f(b_n)\cdot f(p_n) > 0\end{cases}
Donde los valores iniciales vienen dados por:
a_0 := a,\quad b_0:=b
Se puede probar que las tres sucesiones convergen al valor de la única raíz del intervalo:
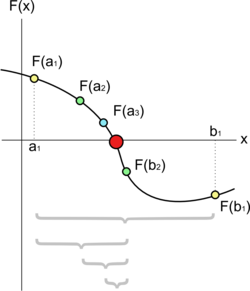\lim_{n \to \infty} a_n = \lim_{n \to \infty} p_n = \lim_{n \to \infty} b_n

Unas cuantas iteraciones del método de bisección aplicadas en un intervalo [a1;b1]. El punto rojo es la raíz de la función.

MÉTODO DE BISECCIÓN

Si f es una función continua sobre el intervalo [a,b] y si f(a) f(b)<0 class="Estilo1" entonces="" nbsp="" span="" style="font-family: 'Times New Roman'; font-size: 14px; font-style: italic;">f
 debe tener un cero en (a,b). Dado que f(a)f(b)<0 cambia="" class="Estilo1" de="" el="" en="" funci="" intervalo="" la="" n="" signo="" span="" style="font-family: 'Times New Roman'; font-size: 14px; font-style: italic;">a,b] y por lo tanto tiene por lo menos un cero en el intervalo. (Véase la figura 5.1)
Esta es una consecuencia del teorema del valor intermedio para funciones continuas, que establece que si f es continua en [a,b] y si k es un número entre f(a) y f(b) , entonces existe por lo menos un c  (a,b) tal que f(c)=k.
(para el caso en que f(a)f(b)<0 class="Estilo1" escoge="" nbsp="" se="" span="" style="font-family: 'Times New Roman'; font-size: 14px; font-style: italic;">k
=0, luego f(c)=0, c  (a,b)).
El método de bisección consiste en dividir el intervalo en 2 subintervalos de igual magnitud, reteniendo el subintervalo en donde f cambia de signo, para conservar al menos una raíz o cero, y repetir el proceso varias veces.
Por ejemplo, suponga que f tiene un cero en el intervalo [a,b].
Primero se calcula el punto medio del intervalo ; después se averigua sí f(a)f(c)<0 .="" a="" c="" cero="" en="" entonces="" es="" f="" lo="" p="" si="" tiene="" un="">
A continuación se renombra a c como b y se comienza una vez más con el nuevo intervalo [a,b], cuya longitud es igual a la mitad del intervalo original.
Si f(a)f(c)>0 , entonces f(c)f(b)<0 a="" caso="" class="Estilo1" en="" este="" nbsp="" renombra="" se="" strong="" style="font-family: 'Times New Roman'; font-size: 14px; font-style: italic;" y="">c
 como a.
En ambos casos se ha generado un nuevo intervalo que contiene un cero de f, y el proceso puede repetirse.
Ejemplo.
La función f(x) = xsenx – 1 tiene un cero en el intervalo [0,2], porque f(0) = -1 yf(2)=0.818595.
Si se denota con entonces c1 = 1. Ahoraf(c1) = f(1) = -0.158529, luego la función tiene un cero en el intervalo [c1, b1] = [1,2] ; se renombra a2=c1 y b2=b1 .
El nuevo punto medio es  y f(c2) = f(1.5) = 0.496242, el cero esta en el intervalo [a2, c2] y se renombra como [a3,b3].
En la tabla de abajo se muestran las primeras nueve iteraciones del método de bisección para f(x)= xsenx –1 con a=0 b=2.
n
Extremo izquierdoan
Extremo derecho bn
Punto medio cn
Valor de la función f(cn)
Error Relativo 
1
0
2
1
-0.158529

2
1
2
1.5
0.496242
0.333333
3
1
1.5
1.25
0.186231
0.2
4
1
1.25
1.125
0.015051
0.111111
5
1
1.125
1.0625
-0.071827
0.0588235
6
1.0625
1.125
1.09375
-0.028362
0.0285714
7
1.09375
1.125
1.109375 
-0.006643
0.0140845
8
1.1093750
1.125
1.1171875
0.004208
0.0069930
9
1.1093750
1.1171875
1.11328125
-0.001216
0.0035087
(c = 1.114157141 es el cero de f(x) = xsenx - 1)
Para detener el método de bisección y dar una aproximación del cero de una función se pueden usar varios criterios (llamados criterios de parada).
Uno de los criterios de parada consiste en examinar si |f(cn)| < , donde  es una tolerancia previamente establecida (por ejemplo  = 10-3). Otro criterio que puede utilizarse es examinar sí 
También se puede usar como criterio de parada el error relativo entre dos aproximaciones del cero de f , 
En el ejemplo anterior si  =0.005, el procedimiento se pararía en la octava iteración con el criterio |f(cn)|<  , ya que:
         |f(c8)| = |f(1.1171875)| = 0.004208 <  = 0.005,
pero si se usa el criterio  , el procedimiento se detendría en la novena iteración porque:
Cuando se generan aproximaciones por medio de una computadora, se recomienda fijar un número máximo de iteraciones N que debería realizar la máquina. Esto con el fin de contar con un resguardo para evitar la posibilidad de que el proceso de cálculo caiga en un ciclo infinito cuando la sucesión diverge (o cuando el programa no esta codificado correctamente). Un algoritmo para el método de bisección es:
Teorema. (Error en el método de bisección).
Si f es continua en [a, b] y f(a) f(b) < 0, el método de bisección genera una sucesión  que aproxima un cero c de f con la propiedad que:  , n 1 (Prueba)

Ejemplo.
Para determinar el número de iteraciones necesarias para aproximar el cero def(x) = xsen x - 1 con una exactitud de 10-2en el intervalo [0,2], se debe hallar un número n tal que:
 < 10-2, es decir , n > 7.643...
se necesitan aproximadamente unas 8 iteraciones.
Observe en la tabla de aproximaciones que el cero de f(x) = xsen x - 1 esc=1.114157141 y c8=1.1171875.
El error real es  = 0.003030359  3x10-3.
El error real es menor que el error dado por el teorema; en la mayoría de casos la cota de error dada por el teorema es mayor que el número de iteraciones que realmente se necesitan. Para este ejemplo, = 0.004782141<10 sup="">-2
 = 0.01

Notas:

  • El método de bisección tiene la desventaja que es lento en cuanto a convergencia (es decir que se necesita un n grande para que  sea pequeño). Otros métodos requieren menos iteraciones para alcanzar la misma exactitud, pero entonces no siempre se conoce una cota para la precisión.
  • El método de bisección suele recomendarse para encontrar un valor aproximado del cero de una función, y luego este valor se refina por medio de métodos más eficaces. La razón es porque la mayoría de los otros métodos para encontrar ceros de funciones requieren un valor inicial cerca de un cero; al carecer de dicho valor, pueden fallar por completo.
  • Resolver una ecuación en una variable como por ejemplo: xex=1 es equivalente a resolver la ecuación xex-1=0 , o a encontrar el cero de la función f(x) = xex-1. Para aproximar el cero de f o la raíz de la ecuación se puede hacer la gráfica de f en una calculadora o usar matlab para determinar un intervalo donde f tenga un cero. También se pueden ensayar números a y b de tal manera que f(a)f(b)<0 .="" caso="" class="Estilo1" de="" el="" nbsp="" para="" span="" style="font-family: 'Times New Roman'; font-size: 14px; font-style: italic;">f
(x) =xex-1 por ejemplo f(0) = -1, f(1) = e-1 1.71828 entonces f tiene un cero en el intervalo [0,1].

  • Cuando hay raíces múltiples, el método de bisección quizá no sea válido, ya que la función podría no cambiar de signo en puntos situados a cualquier lado de sus raíces. Una gráfica es fundamental para aclarar la situación. En este caso sería posible hallar los ceros o raíces trabajando con la derivada f’(x), que es cero en una raíz múltiple.

    •  

    Publicado por en

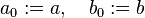
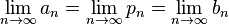
    No hay comentarios:

    Publicar un comentario

    Suscribirse a: Enviar comentarios (Atom)