viernes, 30 de octubre de 2015

Algoritmos

Algoritmos de búsqueda de raíces

método del punto fijo es un método iterativo que permite resolver sistemas de ecuaciones no necesariamente lineales. En particular se puede utilizar para determinar raíces de una función de la forma f(x), siempre y cuando se cumplan los criterios de convergencia.

Descripción del método

El método de iteración de punto fijo, también denominado método de aproximación sucesiva, requiere volver a escribir la ecuación f(x)=0 en la forma x=g(x).

Llamemos x^* a la raíz de f. Supongamos que existe y es conocida la función g tal que:
f(x) = x - g(x)  \forall x del dominio.
Entonces:
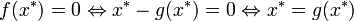
f(x^*)= 0 \Leftrightarrow x^* - g(x^*) = 0 \Leftrightarrow x^* = g(x^*)

Tenemos, pues, a x^* como punto fijo de g.

Procedimiento

El procedimiento empieza con una estimación o conjetura inicial de x, que es mejorada por iteración hasta alcanzar la convergencia. Para que converja, la derivada (dg/dx) debe ser menor que 1 en magnitud (al menos para los valores x que se encuentran durante las iteraciones). La convergencia será establecida mediante el requisito de que el cambio en x de una iteración a la siguiente no sea mayor en magnitud que alguna pequeña cantidad ε.

Algoritmo para iteración de punto fijo

1. Se ubica la raiz de f(x) analizando la gráfica.
2. Se despeja de manera: x=g(x) .
3. Obtenemos de x=g(x) su derivada g\prime(x).
4. Resolviendo la desigualdad -1 ≤ g\prime(x) ≤ 1 obtenemos el rango de valores en los cuales esta el punto fijo llamado R.
5. Con R buscamos la raíz en g(x), es decir g(R)=R haciendo iteración de las operaciones.

Ejemplo 1

Sea f(x)=x^2-5x+3 una función, encuentre la raíz.
Ubicamos la ráiz analizando la gráfica.
Pfijo1
Obtenemos x=g(x):
x= \sqrt{5x-3}
Después obtenemos la derivada de la función:
{dg \over dx}={5 \over 2\sqrt{5x-3}}
Entonces resolvemos las desigualdades:
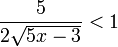
{5 \over 2\sqrt{5x-3}}<1
La solución es:
({37 \over 20},\infty)
{5 \over 2\sqrt{5x-3}}>-1
La solución es:
({3 \over 5},\infty)
O visto de otra manera, vemos que en la gráfica de la derivada existen valores entre -1 y 1:
Pfijo2
Ya que se tienen los valores del rango R, encontramos la raíz haciendo la iteración de las operaciones:
Pfijo3
En la tabla se puede ver el valor que en este caso se usó de R, la iteración consiste en usar ese valor en x=g(x) para obtener los siguientes valores haciendo la misma operación usando el valor anterior.
Después de un número considerable de iteraciones obtenemos la raíz en 4.30268775.

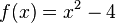
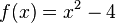
Los dos puntos fijos, marcados en rojo, de la función f(x) = x^2 - 4

5.4. MÉTODO DE PUNTO FIJO

El Método de Punto Fijo (también conocido como iteración de punto fijo), es otro método para hallar los ceros de f(x). Para resolver f(x) = 0, se reordena en una forma equivalente:
f(x) = 0
x - g(x) = 0
x = g(x)
Observe que si c es un cero de f(x), f(c)=0 y c=g(c). (Siempre que se tenga c=g(c) se dice que c es un punto fijo de la función g). Para aproximar un cero de f se utiliza la iteración de punto fijo (1) xn+1 = g(xn) , n = 0, 1, 2, 3, . . .
donde x0 es una aproximación inicial del cero de f.
Ejemplo.
f(x) = x2 - 2x - 3 = 0, tiene dos ceros. x = 3 y x = -1
Supóngase que se reordena para lograr la forma equivalente:

Si se comienza con x0 = 4 y se itera con la iteración de punto fijo (1), los valores sucesivos de x son:
parece que los valores convergen a x = 3.
Otro reordenamiento de f(x) = 0 es :
Si nuevamente se comienza con x0 = 4, los valores sucesivos de x son:
parece que ahora x converge al otro cero de f, x = -1.
Considérese un tercer reordenamiento
Comenzando de nuevo con x0 = 4 se obtiene:
x0 = 4
x1 = 6.5
x2 = 19.625
x3 = 191.070
resulta evidente que las iteraciones son divergentes.
La diferencia en el comportamiento de los tres reordenamientos se puede apreciar considerando las gráficas en los tres casos. El punto fijo de x = g(x) es la intersección de la recta y = x, y la curva y = g(x). En la figura 5.5 se presentan los tres casos. Se comienza en el eje x con x0, se efectúa un desplazamiento vertical hacia la curva, luego uno horizontal hacia la recta y = x, luego uno vertical hacia la curva y nuevamente una horizontal hacia la recta. Este proceso se repite hasta que los puntos en la curva convergen a un punto fijo o bien divergen. Parece que los diferentes comportamientos dependen de que la pendiente de la curva sea mayor, menor o de signo opuesto a la pendiente de la recta (que es igual a 1)
Cuando se tiene la ecuación f(x) = 0, existen muchas formas de reordenarla en la forma x = g(x), por ejemplo para la ecuación anterior x2-2x-3 = 0 otras alternativas son:
**

Una pregunta que surge en este momento es ¿cuál de las funciones g sirve para aproximar el punto fijo de g? (o en forma equivalente el cero de f) . A continuación se presenta un teorema que da condiciones suficientes para la existencia y unicidad del punto fijo de una función.

Teorema 1.

Si g es continua [a,b] y g(x) [a,b] para toda x [a,b], entonces g tiene un punto fijo en [a,b].
Y si además g’(x) existe en (a, b) y existe una constante positiva K < 1 con |g'(x)|  K, para todo x (a,b), entonces el punto fijo en [a,b] es único.
Ejemplo.
La función g(x)=(x2-3)/2 en el intervalo [2,4] tiene un punto fijo único. c=3 es un punto fijo de g porque 
Observe que g'(x)=x y en el intervalo [2,4] g'(x)>0. g es creciente y g(x) [1/2 ,6.5], además |g'(x)| 1. (ya que g'(x)=x y x (2,4)).
Esto demuestra que las hipótesis del teorema 1 son suficientes para garantizar un punto fijo único, pero no son necesarias.
El siguiente resultado da algunas pistas sobre los procedimientos que se deben seguir y algunos que se deben excluir para escoger funciones que produzcan sucesiones que converjan a un punto fijo.

Teorema 2

Sea g una función continua en [a,b] tal que g(x)  [a,b] para toda x en [a,b].Además suponga que existe g' en (a,b) y una constante positiva K<1 tal que|g'(x)|K, para toda x  (a,b), entonces para cualquier número x0 en (a,b), la sucesión definida por xn+1=g(xn), converge al único punto fijo x en [a,b].

Corolario.

Si g satisface las hipótesis del teorema 2, una cota para el error al aproximar el punto fijo x de g por xn es:

(Demostracion)
Ejercicio 1.
Aplique el teorema 2 para demostrar que tiene un punto fijo único en [2,4]. Use el corolario para estimar la cantidad de iteraciones necesarias para lograr una exactitud de 10-2 y después compare esta estimación teórica con la cantidad que realmente se requiere, use x0=3.5.
Solución:
(Nota)
Luego, g(x)  [g(2),g(4)] = [2.65, 3.32]
Por lo tanto g(x)  [a,b] = [2,4] 
Además , porque g'(x) es decreciente y x (2,4)
Como |g'(x)|  K = 0.378 < 1 el punto fijo de g es único en [2, 4].
Para determinar aproximadamente el número de iteraciones necesarias para lograr una exactitud de 10-2 se usa el corolario ,
a = 2
b = 4
x0 = 3.5
 |xn - x|  (0.378)n máx {1.5, 0.5}
k = 0.378
 |xn - x|  (0.378)n(1.5)
 
Como el error debe ser menor que 10-2 entonces
        (0.378)n(1.5) < 10-2
        n > 5.15042...
Por lo tanto se necesitan unas seis iteraciones para lograr una aproximación exacta dentro de 10-2.
Este ejercicio ya se resolvió al comienzo de esta sección y se obtuvo x5=3.00381.
Observe que el error real es | x5 - x| = |3.00.81 - 3| = 0.00381 < 10-2 = 0.01.
Cabe señalar que el corolario no da más que una cota del número de iteraciones necesarias. En la mayoría de casos se requiere un número menor de iteraciones.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)